P12547 [UOI 2025] Simple Subsequence 题解

介绍一种比较糖的维护方式。

首先区间可以从左到右贪心匹配，保证前缀和 \(\ge 0\) 即可。最终折线有一个最大值 \(mx\)，和最终值 \(now\)。那么我们删去最后的 \(mx - now\) 个 \(-1\) 即可。化一下式子，答案就是 \(2c_1 - mx\)，其中 \(c_1\) 是区间中 \(1\) 的数量。

现在就是要维护区间匹配过程中的 \(mx\) 即可。即画一条从原点开始的折线，如果碰到 \(x\) 轴就不减了，整个过程的最大值。下面是我在模拟赛时想到的做法：

建线段树，每个线段树上维护节点代表区间的 \(mx\)，左右边到最低点的距离 \(L,R\)，还有不考虑和 \(0\) 取 \(\max\) 时，折线的最大值 \(mx2\)。

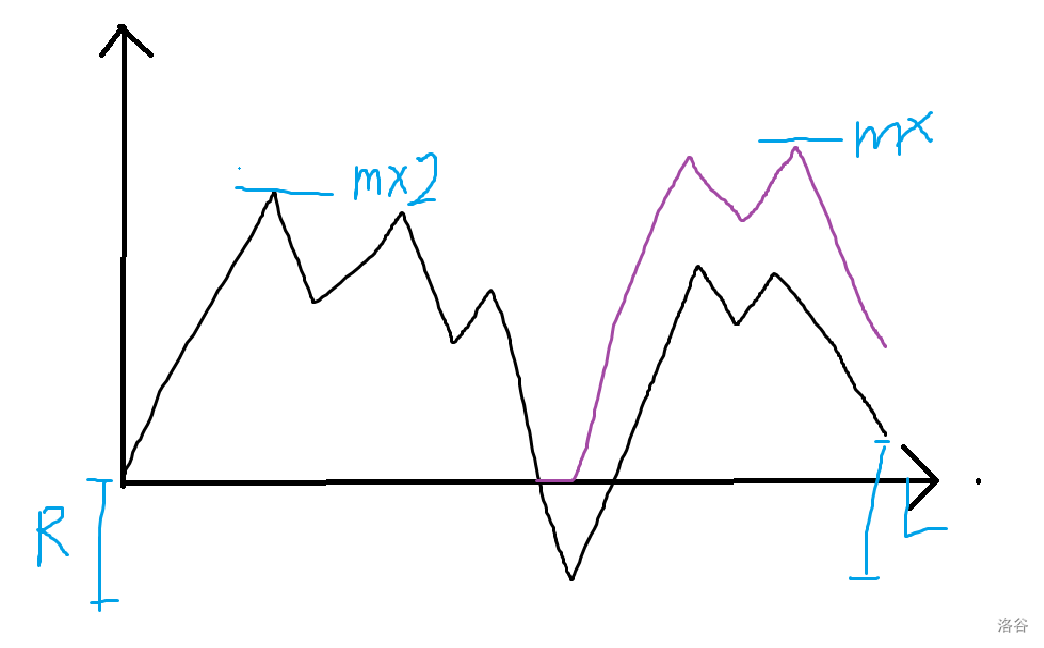
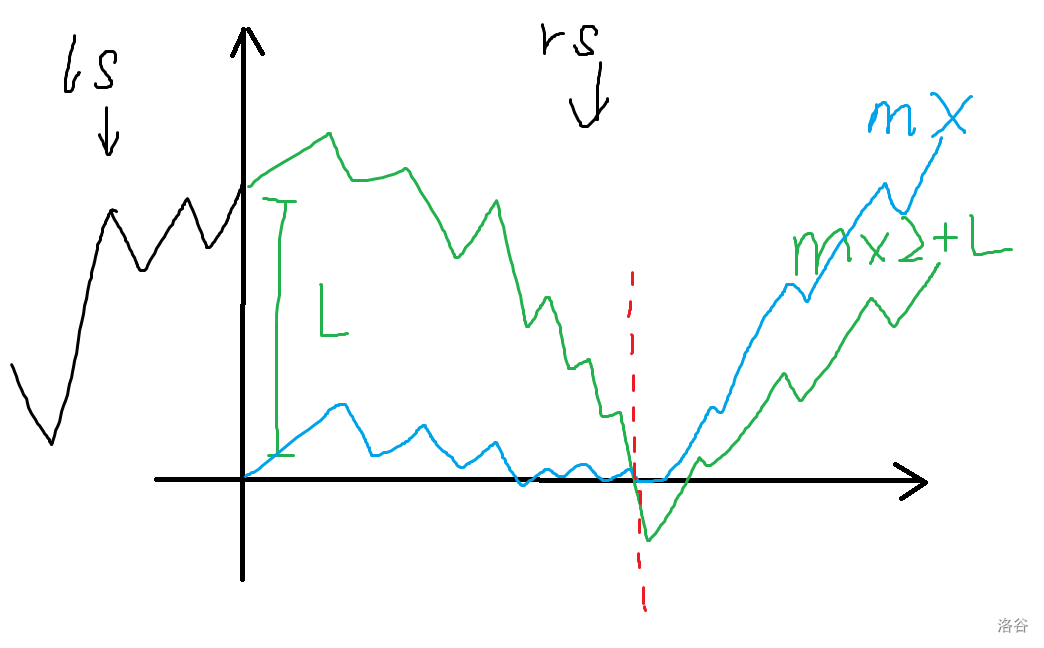
合并左右儿子的时候，\(L,R,mx2\) 均可以直接计算。对于 \(mx\)，有 \(mx = \max(mx_{ls},mx_{rs},R_{ls} + mx2_{rs})\)

对于右儿子的过程，第一次碰到 \(x\) 轴前，\(mx2\) 是正确的，后面 \(mx\) 是正确的，其他时候答案一定更小。所以信息就维护对了。

inline void PushUp(node &i,node ls,node rs){
  i.c1=ls.c1+rs.c1;
  i.R=ls.R+std::max(0,rs.R-ls.L);
  i.L=rs.L+std::max(0,ls.L-rs.R);
  i.mx1=std::max({ls.mx1,ls.L+rs.mx2,rs.mx1});
  i.mx2=std::max(ls.mx2,rs.mx2+ls.L-ls.R);
}