多项式复合集合幂级数

写完过了一个月忘干净了。

按照题解区第二篇题解的思路，我们有这样的转移：

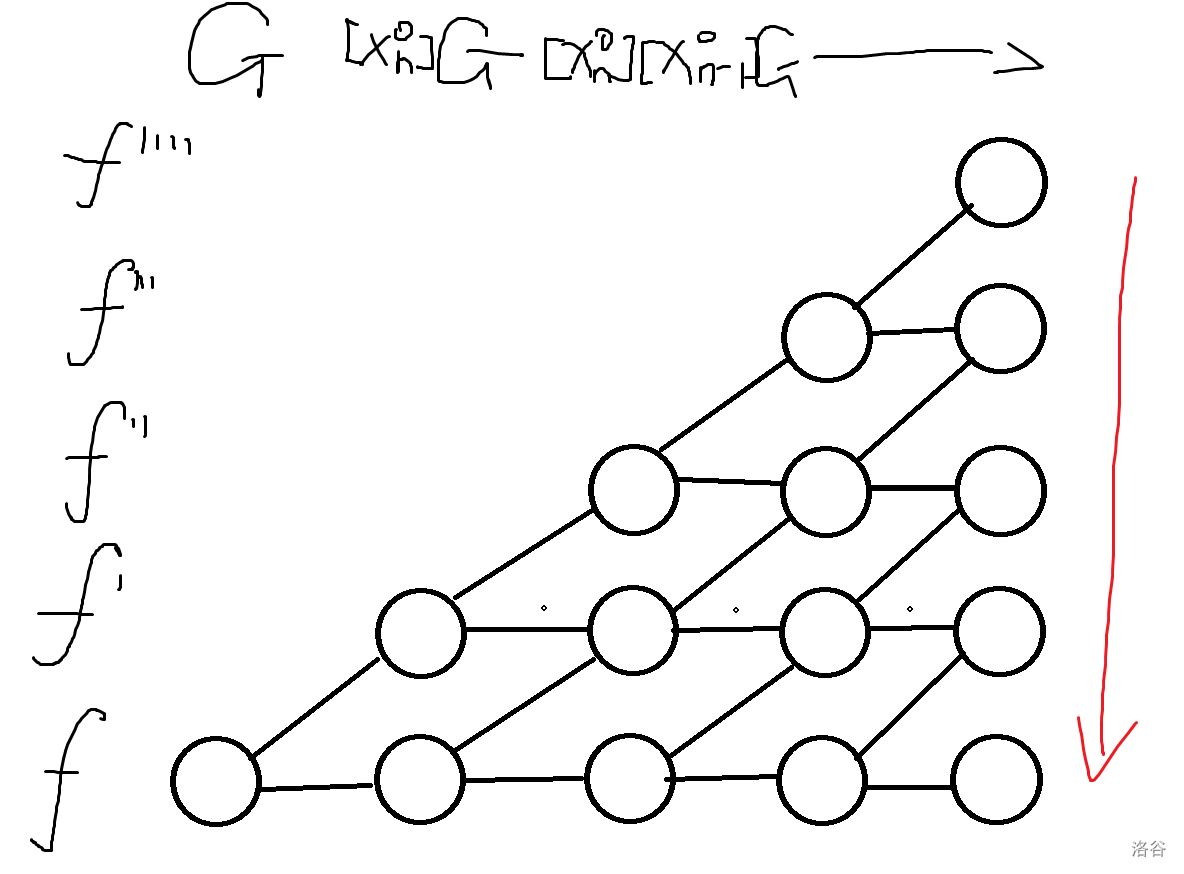
我们考虑从上到下转移，我们称忽略 \(i \sim n\) 的所有变量的集合幂级数 \(G\) 为 \({}^iG\)。

第 \(i\) 行的第一项（最右边对应的项）就是 \(f^{(n)}(0)\)。后面的顺次存在数组里面，需要 \(2n\) 的空间。

直接转移即可。对于上图中从右往左数第 \(i\) 列（\(0\) 开始标号），从上一行转移的转移系数是 \([x_i^1]{}^{i+1}G\)。

实际上这就是按照 \(highbit\) 分类之后的 \(G\)。要分别求出每一段 FWT 后的结果比较麻烦，但是我们可以一次 FWT 求出。具体地其实只需要每层 FWT 的时候把第一组跳过就可以了。就是下面代码 \(op = 1\)：

inline void FWT(int *a,int x,int op){
    for(int t=2,k=1;t<=(1<<n);t<<=1,k<<=1)
        for(int i=op*t;i<(1<<n);i+=t)
            for(int j=0;j<k;j++)Add(a[i+j+k],1ll*a[i+j]*x%mod);
}

算完这个直接转移就行。

for(int t=0;t<=n;t++){
    for(int j=0;j<=n;j++)
        for(int i=0;i<(1<<t);i++)b[j][i]=a[j][i],a[j][i]=0;
    a[0][0]=f[t][0];
    for(int i=1;i<=t;i++){
        for(int j=(1<<(i-1));j<(1<<i);j++){
            for(int k=0;k<=t;k++){
                for(int l=0;l<=k;l++)
                    Add(a[k][j],1ll*b[l][j-(1<<(i-1))]*g[k-l][j]%mod);
                Add(a[k][j],a[k][j-(1<<(i-1))]);
            }
        }
    }
}

最后是常数优化，更改一下循环的顺序，小的一维尽量在前面。

加的时候用 \(\text{unsigned long long}\) 存总和，每 \(18\) 次加法取模一次。（其实每 \(n\) 次取模一次就完事儿了，基本不可能卡的很满）。这个能快非常多。