P8261 [CTS2022] 袜子 题解

lxl 上课讲的，基于随机的，\(O(n\sqrt m)\) 做法。

首先将点和线反过来，就是本来是 \(Ax + By + C < 0\)，现在给他变成 \(y\dfrac{B}{A} + 1\cdot\dfrac{C}{A} + x < 0\)。（\(A < 0\) 或 \(A = 0\) 时会有所不同，直接分成三部分做就行）。

现在我们要算的是，只看一种颜色的半平面时，如果一个点被半平面覆盖了 \(k\) 次，那么它就将 \(k^2\) 加进答案里面去。

考虑 \(\text{kd-tree}\) 直接暴力修改，但是这样看起来标记不大好下放，因为不同颜色之间标记可能会互相影响。我们考虑如下做法：对于一种颜色的半平面，我们先把他们都拿出来在 \(\text{kd-tree}\) 上面暴力打 \(\text{tag}\)，打完之后把修改涉及到的所有点都拿出来全部 \(\text{pushdown}\) 一遍，这样一个点上方就没有未下放的 \(\text{tag}\) 了，直接将答案加上 \(\text{tag}^2\)，并将 \(\text{tag}\) 清空即可。

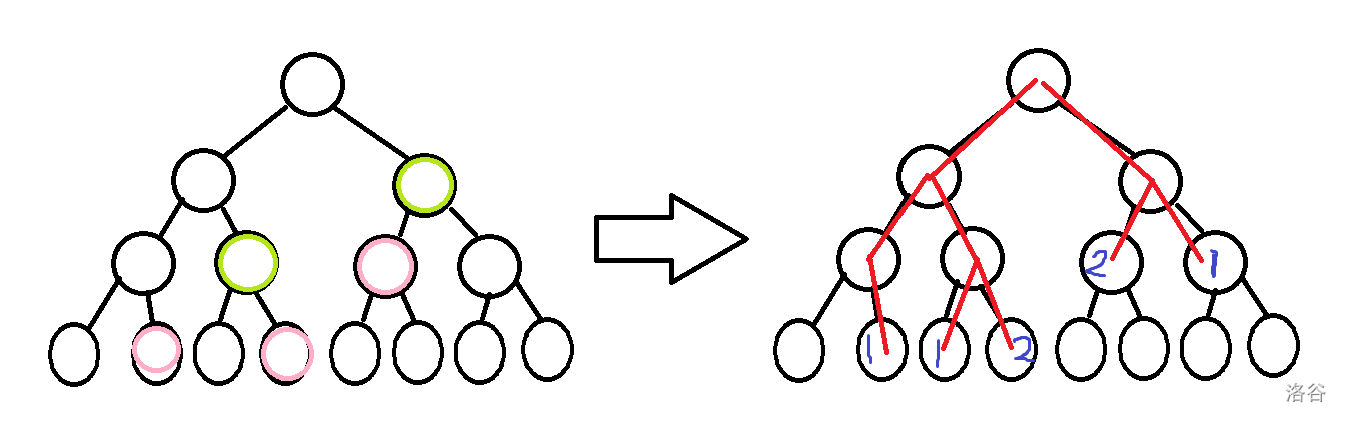
（偷懒画成 \(\text{leafy}\) 的，这样比较好理解）图中绿色和粉色是两次修改，涂颜色的节点打上子树 \(+1\) 的 \(\text{tag}\)。后面图中红色是 \(\text{pushdown}\) 的路径，蓝色是最终一个节点的子树被加了多少（该节点子树的答案都应被加上 \(\text{tag}^2\)）。

这样时间复杂度是对的，由于数据随机，\(\text{kd-tree}\) 一次修改只会改 \(O(\sqrt m)\) 个节点，后面的操作只不过是又遍历一遍，时间复杂度不受影响。

至此复杂度就变成了 \(O(n \sqrt m)\)（注意我们先将点和半平面互换了）。由于常数太大不能通过此题（qoj 3s 过了，洛谷太慢了）。

一些卡常技巧：

• \(\text{kd-tree}\) 写成非 \(\text{leafy}\) 的，这样看似要多维护一些东西，实则更快一些。

• 如果一种颜色只出现一次就直接打 \(\text{tag}\)，这个有一点点用。

• 一种颜色的半平面按照斜率排序，这个据说是访存连续，但没什么用，应该是颜色数比较多。

至此你可以获得 \(55 \sim 85\) 分，然后是最重要的一招：分块，然后逐块处理。

把 \(\text{kd-tree}\) 的前几层删了，此时原序列变成若干块，对每一块分别做修改，也就是逐块处理，这样由于每次修改的点数很少，能卡进一些神秘的缓存然后就跑得飞快，最慢点不到 5s，立马变成洛谷最优解。

卡常确实有很大学问呐。