AT_arc186_d [ARC186D] Polish Mania 题解

先说结论，一个序列合法当且仅当：

\[\sum A_i = n - 1 \]

\[\forall m<n,\sum\limits_{i=1}^{m} A_i \ge i \]

证明可以考虑将序列看成一棵树，第 \(i\) 个点有 \(A_i\) 个儿子，\(A_i = 0\) 就是叶子节点。这样首先一棵树有 \(n-1\) 条边，然后往上接节点的时候必须保证当前边数大于点数减一,否则下一个节点就没地方放了。

考虑对这样的序列计数，考虑转化成格路。并且要求不走过 \(y = x - 1\) 这条直线（\(A_n\) 一定为 \(0\)，直接把第 \(n\) 个扔掉），直接反射容斥即可。

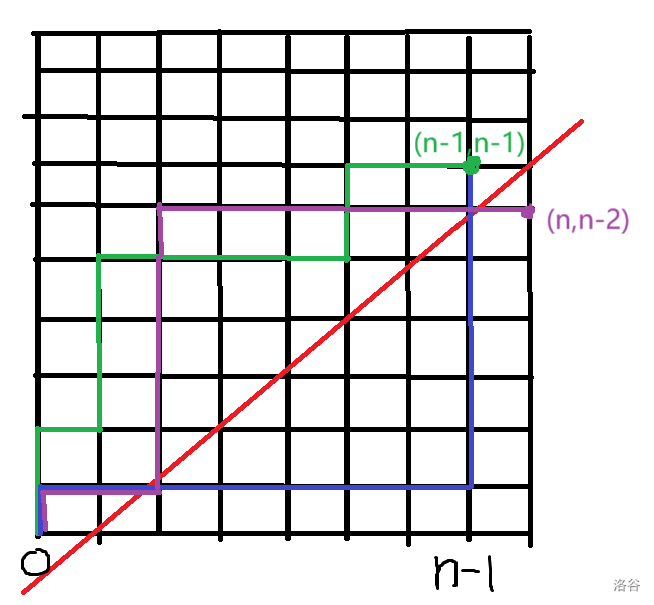
如上图，红色是不能碰的直线，绿色是合法路径（其中 \(x = i\) 时上升了多少就是 \(a_{x+1} - a_x\)），蓝色是不合法路径，紫色是反射后的不合法路径。

对于字典序小于某个序列的限制，我们仿照数位 DP，对于 第 \(i\) 位，我们枚举第 \(i\) 位，计数前 \(i-1\) 位达到限制，第 \(i\) 位严格 \(< A_i\) 的方案数。别忘了统计整个序列是否合法即全达到限制的方案。

复杂度看起来是 \(O(n^2)\) 的。但是 \(\sum A_i \ge n\) 时一定不合法，因此复杂度 \(O(n)\)。

submission