从“树”到“平衡二叉搜索树”

树：一个每条边都是桥的连通图。

二叉树：一棵有根树。每个节点的分支数量 $\leq 2$ 个，分支称为“左子树”和“右子树”，顺序不能随意颠倒。
特别的，wikipedia 提到“很多人喜欢使用“有根二叉树”而非二叉树，以强调二叉树是有根的，但归根结底二叉树是有根的”。

二叉搜索树：一棵二叉树。每个内部节点的键大于该节点左子树中的所有键，而小于该节点右子树中的所有键。
二叉搜索树最常见的名字，Binary Search Tree，大家通常喜欢写作 BST 。有些地方也会叫做“有序二叉树”或者“排序二叉树”，指的都是同一种树。

显然，基于 BST 的定义，BST 的子树也是 BST 。

定理 1 ：BST 中左链上的最左节点为最小节点。
证明：
设左链上的节点为 $root=N_0, N_1, \cdots, N_k$ ，对于 $0 \leq i < k$, $N_{i + 1}$ 是 $N_{i}$ 的左儿子，$N_{k}$ 是左链上的最左节点。
首先有 $N_k < N_{k - 1} < \cdots < N_{0} = root$ 。$\forall$ 非左链节点 $z$ ，$\exists j, 0 \leq j \leq k$ 满足 $z$ 是 $N_{j}$ 的右子树节点。
则 $N_{k} \leq N_{j} < z$ ，即 BST 中左链上的最左节点是 BST 中的最小节点。
$\square$

实现：

\[\hspace{-32em}\begin{aligned} 1: \ &\text{findMinNode}(root) \\ 2: \ &\quad \textbf{while} \ root.\text{left} \neq \text{NIL} \ \textbf{do} \\ 3: \ &\quad\quad root \leftarrow cur.\text{left} \\ 4: \ &\quad \textbf{return} \ root \end{aligned} \]

定理 2 ：BST 中右链上的最右节点为最大节点。
证明：
设右链上的节点为 $root=M_0, M_1, \cdots, M_l$ ，对于 $0 \leq i < l$, $M_{i + 1}$ 是 $M_{i}$ 的右儿子，$M_{l}$ 是右链上的最右节点。
首先有 $M_l > N_{l - 1} > \cdots > M_{0} = root$ 。$\forall$ 非右链节点 $z$ ，$\exists j, 0 \leq j \leq l$ 满足 $z$ 是 $M_{j}$ 的左子树节点。
则 $M_{k} \geq M_{j} > z$ ，即 BST 中右链上的最右节点是 BST 中的最大节点。
$\square$

实现：

\[\hspace{-32em}\begin{aligned} 1: \ &\text{findMaxNode}(root) \\ 2: \ &\quad \textbf{while} \ root.\text{right} \neq \text{NIL} \ \textbf{do} \\ 3: \ &\quad\quad root \leftarrow root.\text{right} \\ 4: \ &\quad \textbf{return} \ root \end{aligned} \]

定理 3 ：BST 的节点 $x$ 的前驱（升序序列中该节点的前一个节点）。

若 $x$ 存在左子树，前驱是左子树上右链的最右节点；
否则前驱是 $x$ 最近的将其置于右子树中的祖先 $y$ 。

证明：
考虑当前的根 $root$ ，他的子树在升序序列中的区间一定为 $[1, n]$ ，令 $L = 1, R = n$ 。
考虑节点 $x$ 的排名为 $k$ ，他在升序序列中的子树区间为 $[l, r]$ 满足 $L \leq l \leq k \leq R$ 。
考虑从根到 $x$ 的路径，每次向左走，当前节点和右子树都比左子树大，则存在一个 $p$ 满足 $r < p \leq R$ ，使得新子树的区间为 $[L, p - 1]$ ，更新 $R \gets p - 1$ ；每次向右走，当前节点和左子树都比其右子树小，则存在一个 $q$ 满足 $L \leq q < l$ ，使得新子树的区间为 $[q + 1, R]$ ，更新 $L \gets q + 1$ 。
显然非 $x$ 的子树节点中，最大的比 $x$ 小的节点在最后一次向右走时出现，且是离 $x$ 最近的将其置于右子树的祖先 $y$ 。

考虑如何找到 $y$ ，自顶向下的方法是从 $root$ 往 $x$ 走，更新右拐的节点，则最后一次更新的节点为 $y$ 。
考虑自底向上的方法，从 $x$ 往根节点走的路径中，若当前节点是其父亲的左儿子则 $x$ 在其父亲的左子树中，若当前节点是其父亲的右儿子则 $x$ 在其父节点的右子树中，于是只需向上跳到第一个节点满足其是父节点的右儿子，则其父亲为离 $x$ 最近的将 $x$ 置于右子树的祖先。

若 $x$ 存在左子树，由于 $x$ 在 $y$ 的左子树中，$x$ 的左子树也一定比 $y$ 小，则 $x$ 的前驱是 $x$ 左子树中的最大节点，即左子树上右链的最右节点。若 $x$ 不存在左子树，则只有非 $x$ 子树的节点可能比 $x$ 小，则 $x$ 的前驱是离它最近的将它置于右子树的节点 $y$ ，即非 $x$ 子树中最大的比 $x$ 小的节点。
$\square$

如果记录 $parent$ 节点，可以从 $x$ 往上跳。实现形式 1：

\[\hspace{-32em}\begin{aligned} 1: \ &\text{predecessor}(x) \\ 2: \ &\quad \textbf{if} \ x.\text{left} \neq \text{NIL} \ \textbf{then} \\ 3: \ &\quad\quad \textbf{return} \ \text{findMaxNode}(x.\text{left}) \\ 4: \ &\quad \textbf{else} \\ 5: \ &\quad\quad \textbf{while} \ x.\text{parent} \neq \text{NIL} \ \textbf{and} \ x = x.\text{parent}.\text{left} \ \textbf{do} \\ 6: \ &\quad\quad\quad x \gets x.\text{parent} \\ 7: \ &\quad\quad \textbf{return} \ x.\text{parent} \end{aligned} \]

如果不记录 $parent$ 节点，则从根往 $x$ 跳。时间复杂度同第一种实现。实现形式 2：

\[\hspace{-32em}\begin{aligned} 1: \ &\text{predecessor}(root, x, pred) \\ 2: \ &\quad \textbf{if} \ root = \text{NIL} \ \textbf{then} \\ 3: \ &\quad\quad \textbf{return} \ \text{NIL} \\ 4: \ &\quad \textbf{if} \ x.\text{key} = root.\text{key} \ \textbf{then} \\ 5: \ &\quad\quad \textbf{if} \ x.\text{left} \neq \text{NIL} \ \textbf{then} \\ 6: \ &\quad\quad\quad \textbf{return} \ \text{findMaxNode}(root.\text{left}) \\ 7: \ &\quad\quad \textbf{else} \ \textbf{return} \ pred \\ 8: \ &\quad \textbf{elseif} \ x.\text{key} < root.\text{key} \ \textbf{then} \\ 9: \ &\quad\quad \textbf{return} \ \text{predecessor}(root.\textbf{left}, x, pred) \\ 10: \ &\quad \textbf{else} \ \textbf{return} \ \text{predecessor}(root.\textbf{right}, x, root) \\ \end{aligned} \]

定理 4 ：BST 的节点 $x$ 的后继（升序序列中该节点的后一个节点）。

若 $x$ 存在右子树，后继是右子树上左链的最左节点；
否则后继是 $x$ 到根的右链段中最近的祖先 $y$ 。

证明：
考虑当前的根 $root$ ，他的子树在升序序列中的区间一定为 $[1, n]$ ，令 $L = 1, R = n$ 。
考虑节点 $x$ 的排名为 $k$ ，他在升序序列中的子树区间为 $[l, r]$ 满足 $L \leq l \leq k \leq R$ 。
考虑从根到 $x$ 的路径，每次向左走，当前节点和右子树都比左子树大，则存在一个 $p$ 满足 $r < p \leq R$ ，使得新子树的区间为 $[L, p - 1]$ ，更新 $R \gets p - 1$ ；每次向右走，当前节点和左子树都比其右子树小，则存在一个 $q$ 满足 $L \leq q < l$ ，使得新子树的区间为 $[q + 1, R]$ ，更新 $L \gets q + 1$ 。
显然非 $x$ 的子树节点中，最小的比 $x$ 大的节点在最后一次向左走时出现，且是离 $x$ 最近的将其置于左子树的祖先 $y$ 。

考虑如何找到 $y$ ，自顶向下的方法是从 $root$ 往 $x$ 走，更新左拐的节点，则最后一次更新的节点为 $y$ 。
考虑自底向上的方法，从 $x$ 往根节点走的路径中，若当前节点是其父亲的右儿子则 $x$ 在其父亲的右子树中，若当前节点是其父亲的左儿子则 $x$ 在其父节点的左子树中，于是只需向上跳到第一个节点满足其是父节点的左儿子，则其父亲为离 $x$ 最近的将 $x$ 置于左子树的祖先。

若 $x$ 存在右子树，由于 $x$ 在 $y$ 的右子树中，$x$ 的右子树也一定比 $y$ 大，则 $x$ 的后继是 $x$ 右子树中的最小节点，即右子树上左链的最左节点。若 $x$ 不存在右子树，则只有非 $x$ 子树的节点可能比 $x$ 大，则 $x$ 的后继是离它最近的将它置于左子树的节点 $y$ ，即非 $x$ 子树中最小的比 $x$ 大的节点。

实现：

\[\hspace{-32em}\begin{aligned} 1: \ &\text{successor}(root, x, pred) \\ 2: \ &\quad \textbf{if} \ root = \text{NIL} \ \textbf{then} \\ 3: \ &\quad\quad \textbf{return} \ \text{NIL} \\ 4: \ &\quad \textbf{if} \ x.\text{key} = root.\text{key} \ \textbf{then} \\ 5: \ &\quad\quad \textbf{if} \ x.\text{left} \neq \text{NIL} \ \textbf{then} \\ 6: \ &\quad\quad\quad \textbf{return} \ \text{findMaxNode}(root.\text{left}) \\ 7: \ &\quad\quad \textbf{else} \ \textbf{return} \ pred \\ 8: \ &\quad \textbf{elseif} \ x.\text{key} < root.\text{key} \ \textbf{then} \\ 9: \ &\quad\quad \textbf{return} \ \text{successor}(root.\textbf{left}, x, pred) \\ 10: \ &\quad \textbf{else} \ \textbf{return} \ \text{successor}(root.\textbf{right}, x, root) \\ \end{aligned} \]

定理 5 ：BST 的中序遍历是二叉树的升序序列。

证明：
对于节点个数为 $1$ 的 BST ，显然成立。
否则由归纳假设，$root$ 的左子树的中序遍历是升序序列 $L_1$ ，$root$ 的右子树的升序遍历是升序序列 $L2$ 。由 $L_1 < root.\text{key} < L_2$ ，则该 BST 的中序遍历 $[L_1, root.\text{key}, L_2]$ 是升序遍历。
$\square$

实现：

\[\hspace{-32em}\begin{aligned} 1: \ &\text{inorderTraversal}(root) \\ 2: \ &\quad \textbf{if} \ root = \text{NIL} \ \textbf{then} \\ 3: \ &\quad \quad \textbf{return} \\ 4: \ &\quad \text{inorderTraversal}(root.\text{left}) \\ 5: \ &\quad \text{print} \ root.\text{key} \\ 6: \ &\quad \text{inorderTraversal}(root.\text{right}) \\ \end{aligned} \]

定理 6 ：BST 中查询 $target$ 。

若 $target = root.\text{key}$ 则目标节点是当前节点；
若 $target < root.\text{left}.\text{key}$ 则目标节点在左子树中；
若 $target > root.\text{right}.\text{key}$ 则目标节点在右子树中；
若访问到了空节点，则目标节点不存在。

证明：
二叉搜索树的性质：中任意节点大于其左子树所有键，小于其右子树所有键。
$\square$

实现：

\[\hspace{-32em}\begin{aligned} 1: \ &\text{search}(root, target) \\ 2: \ &\quad \textbf{if} \ root = \text{NIL} \ \textbf{then} \\ 3: \ &\quad\quad \textbf{return} \ \text{FALSE} \\ 4: \ &\quad \textbf{if} \ target = root.\text{key} \ \textbf{then} \\ 5: \ &\quad\quad \textbf{return} \ \text{TRUE} \\ 6: \ &\quad \textbf{elseif} \ traget < root.\text{kty} \ \textbf{then} \\ 7: \ &\quad\quad \textbf{return} \ \text{search}(root.\text{left}, target) \\ 8: \ &\quad \textbf{else} \ \textbf{return} \ \text{search}(root.\text{right}, target) \\ \end{aligned} \]

定理 7 ：BST 中插入 $target$ 。

若 $target$ 等于当前节点，则让当前节点的键计数加一。
若 $target$ 小于当前节点，则向左子树插入，插入完成后更新该节点的左儿子为左子树的根。
若 $target$ 大于当前节点，则向右子树插入，插入完成后更新该节点的右儿子为右子树的根。
若 $target$ 在空节点上，则更新该空节点为当前节点。

证明：
二叉搜索树的性质：中任意节点大于其左子树所有键，小于其右子树所有键。
若 $target$ 等于当前节点，让当前节点的计数加一，不影响当前节点子 BST 的性质。
若 $target$ 小于当前节点，往左子树插入不影响当前节点子 BST 的性质。插入操作影响左子树结构，插入结束后，当前节点自然应当更新成左子树的根。
若 $target$ 大于当前节点，往右子树插入不影响当前节点子 BST 的性质。插入操作影响右子树结构，插入结束后，当前节点自然应当更新成右子树的根。
若 $target$ 抵达空节点，则让该空节点更新为 $target$ ，因为当前节点子 BST 只有一个节点，不影响性质。
$\square$

更精细地分析，插入操作会且只会影响叶子的结构，故而只会影响叶子的儿子。但这个性质在算法层面不重要。

实现：

\[\hspace{-32em}\begin{aligned} 1: \ &\text{insert}(root, target) \\ 2: \ &\quad \textbf{if} \ root = \text{NIL} \ \textbf{then} \\ 3: \ &\quad\quad \textbf{return} \ \text{newNode}(target) \\ 4: \ &\quad root.\text{size} \gets root.\text{size} + 1 \\ 5: \ &\quad \textbf{if} \ target = root.\text{key} \ \textbf{then} \\ 6: \ &\quad\quad root.\textbf{cnt} \gets root.\textbf{cnt} + 1 \\ 7: \ &\quad \textbf{elseif} \ target < root.\text{key} \ \textbf{then} \\ 8: \ &\quad\quad root.\text{left} \gets \text{insert}(root.\text{left}, target) \\ 9: \ &\quad \textbf{else} \\ 10: \ &\quad\quad root.\text{left} \gets \text{insert}(root.\text{right}, target) \\ 11: \ &\quad \textbf{return} \ root \\ \end{aligned} \]

定理 8 ：BST 中删除 $target$ 。

若 $target$ 等于当前节点且键数大于 $1$ ，则键数减 $1$ ；否则访问某棵子树
1.1 若左子树存在，让当前节点的键等于其前驱的键，递归向左子树删除该前驱。
1.2 若右子树存在，让当前节点的键等于其后继的键，递归向右子树删除该后继。
若 $target$ 小于当前节点，则往左子树删除，删除完成后更新该节点的左儿子。
若 $target$ 大于当前节点，则往右子树删除，删除完成后更新该节点的右儿子。
若 $target$ 在空节点上，则不存在 $target$ 。

删除 $target$ 之前需要先查询一遍其是否在 BST 中，否则删除失败需要回溯删除时进行过的操作。

证明：
考虑定位到需要的删除点后，若该节点是叶子则可直接删除。
否则可以提升左子树中该节点的前驱并向左子树递归删除该前驱，或可以提升右子树中该节点的后继并向右子树递归删除该后继。不影响该节点位置的 BST 性质：左子树的所有键小于该节点，右子树的所有键小于该节点。删除操作结束后，对应子树的结构改变，该节点的对应儿子自然应该更新成对应子树的根节点。
$\square$

存在一个显然的特例，若删除的节点不存在左子树，则可以直接让该节点的右子树作为当前的子树；若删除的节点不存在左子树，则可以直接让该节点的左子树作为当前的子树。但这个特例并不关键。

实现：

\[\hspace{-32em}\begin{aligned} 1: \ &\text{remove}(root, target) \\ 2: \ &\quad \textbf{if} \ root = \text{NIL} \ \textbf{then} \\ 3: \ &\quad\quad \textbf{return} \ root \\ 4: \ &\quad root.\text{szie} \gets root.\text{szie} - 1 \\ 5: \ &\quad \textbf{if} \ target = root.\text{key} \ \textbf{then} \\ 6: \ &\quad\quad \textbf{if} \ root.\text{cnt} > 1 \ \textbf{then} \\ 7: \ &\quad\quad\quad root.\text{cnt} \gets root.\text{cnt} - 1 \\ 8: \ &\quad\quad \textbf{elseif} \ root.\text{left} \neq \text{NIL} \ \textbf{then} \\ 9: \ &\quad\quad\quad predecessor = \text{findMaxNode}(root.\text{left}) \\ 10: \ &\quad\quad\quad root.\text{key} \gets predecessor.\text{key} \\ 11: \ &\quad\quad\quad root.\text{left} = \text{remove}(root.\text{left}, predecessor.\text{key}) \\ 12: \ &\quad\quad \textbf{else} \\ 13: \ &\quad\quad\quad successor = \text{findMinNode}(root.\text{right}) \\ 14: \ &\quad\quad\quad root.\text{key} \gets successor.\text{key} \\ 15: \ &\quad\quad\quad root.\text{right} = \text{remove}(root.\text{right}, successor.\text{key}) \\ 16: \ &\quad \textbf{elseif} \ target < root.\text{key} \ \textbf{then} \\ 17: \ &\quad\quad root.\text{left} \gets \text{remove}(root.\text{left}, target) \\ 18: \ &\quad \textbf{else} \\ 19: \ &\quad\quad root.\text{right} \gets \text{remove}(root.\text{right}, target) \\ 20: \ &\quad \textbf{return} \ root \\ \end{aligned} \]

定理 9 ：BST 中查询 $target$ 的排名（排名从 1 开始）。

若 $target$ 小于当前节点，则返回左子树统计的排名。
若 $target$ 大于当前节点，则计算右子树和当前节点的键数，加上右子树统计的排名。
若 $target$ 等于当前节点，则返回左子树的键数 + 1 。

查询 $target$ 的排名之前需要先查询一遍其是否在 BST 中，否则会返回错误排名。

证明：
这种 BST 中查询 $target$ 的排名的方法，本质上是通过树形 DP 解决（当然也有自顶向下的方法，但需要显示维护一个答案）。
如果 $target$ 小于当前节点，则当前子树的答案即其左子树贡献的排名。$dp[cur] \gets dp[cur.\text{left}]$ 。
如果 $target$ 大于当前节点，则当前子树的答案即左子树贡献的大小 + 当前节点贡献的大小 + 右子树贡献的排名。$dp[cur] \gets SZ(cur.\text{left}) + cur.\text{cnt} + dp[cur.\text{right}]$ 。
如果 $target$ 等于当前节点，则当前子树的答案即 $target$ 在当前子树中的排名。其排名在区间 $[text{sz}(cur.\text{left}) + 1, cur.\text{left}.\text{sz} + SZ(cur.\text{left}) + cur.\text{cnt}]$ 中，不妨选择 $text{sz}(cur.\text{left}) + 1$ 。$dp[cur] \gets SZ(cur.\text{left}) + 1$ 。
$\square$

BST 中查询 $target$ 的排名我们通常并不使用空间维护所有子树的答案，即记录 dp 表。因为树的结构会频繁改变，导致查询需要重新 dp 。

这里定义 SZ 数组可以让我们避免“通过讨论子节点是否为空从而避免访问空间点”。

实现：

\[\hspace{-32em}\begin{aligned} 1: \ &\text{SZ}(root) \\ 2: \ &\quad \textbf{if} \ root = \text{NIL} \ \textbf{then} \\ 3: \ &\quad\quad \textbf{return} \ 0 \\ 4: \ &\quad \textbf{else} \ \textbf{return} \ root.\text{size} \\ \\ 1: \ &\text{queryRank}(root, target) \\ 2: \ &\quad \textbf{if} \ root = \text{NIL} \ \textbf{then} \\ 3: \ &\quad\quad \textbf{return} \ 0 \\ 4: \ &\quad \textbf{if} \ target < root.\text{key} \ \textbf{then} \\ 5: \ &\quad\quad \textbf{return} \ \text{queryRank}(root.\text{left}, target) \\ 6: \ &\quad \textbf{elseif} \ traget > root.\text{key} \ \textbf{then} \\ 7: \ &\quad\quad \textbf{return} \ \text{SZ}(root.\text{left}) + \text{queryRank}(root.\text{right}, target) \\ 8: \ &\quad \textbf{else} \ \textbf{return} \ \text{SZ}(root.\text{left}) + 1 \\ \end{aligned} \]

定理 10 ：BST 查询排名为 $k$ 的节点。

若 $k$ 小于等于左子树的大小，则目标节点是左子树中排名为 $k$ 的节点。
若 $k$ 大于左子树的大小，并小于等于左子树的大小 + 当前节点的键数，则目标点是当前节点。
若 $k$ 大于左子树的大小 + 当前点的键数，则目标点是右子树中排名为 $k - \text{SZ}(cur.\text{left}) - cur.\text{cnt}$ 的节点。

显然我们应该首先确定 $k$ 在区间 $[1, SZ(root)]$ 内。

证明：
这里我们需要一直显示维护参数 $k$ ，所以使用自顶向下的方法。
若 $k$ 小于等于左子树的大小，则当前子树的 $k$ 个最小节点必然都在左子树中，自然当前子树中排名为 $k$ 的节点是左子树中排名为 $k$ 的节点。
若 $k$ 大于左子树的大小，并小于等于左子树的大小 + 当前节点的键数，则目标节点不在左子树中，且在左子树和当前节点的集合中，即目标节点是当前节点。
若 $k$ 大于左子树的大小 + 当前节点的键数，则目标节点只能在右子树中。由左子树和当前节点总共 $SZ(cur.\text{left} + cur.\text{cnt})$ 个键都小于 $k$ ，且右子树的键大于这些键，则目标节点是右子树中排名为 $k - SZ(cur.\text{left}) + cur.\text{cnt}$ 的节点。
$\square$

实现：

\[\hspace{-32em}\begin{aligned} 1: \ &\text{queryKth}(root, k) \\ 2: \ &\quad \textbf{if} \ root = \text{NIL} \ \textbf{then} \\ 3: \ &\quad\quad \textbf{return} \ NIL \\ 4: \ &\quad v \gets \text{SZ}(root.\text{left}) \\ 5: \ &\quad \textbf{if} \ k \leq v \ \textbf{then} \\ 6: \ &\quad\quad \textbf{return} \ \text{queryKth}(root.\text{ left} \\ 7: \ &\quad \textbf{elseif} \ k \leq v + root.\text{cnt} \ \textbf{then} \\ 8: \ &\quad\quad \textbf{return} \ root \\ 9: \ &\quad \textbf{else} \ \textbf{return} \ \text{queryKth}(root.\text{right}, k - v - root.\text{cnt}) \\ \end{aligned} \]

二叉搜索树使得可以通过树来存储和操作键。
数据随机情况下，$n$ 个节点的 BST 高度可以达到 $O(\log n)$ ，此时所有操作也是 $O(\log n)$ 的。
但可以构造特殊数据，使得 BST 构造出来的高度为 $O(n)$ ，此时所有操作的时间复杂度都是 $O(N)$ 的。
进而有一个想法：我们插入和删除键的时候，调整子树结构，使其变得尽量扁平不就好了？这就是平衡二叉搜索树的想法。

默认语境下也称为名字平衡二叉树（默认了是搜索树），是一种自平衡的二叉搜索树。由于历史原因，平衡二叉搜索树有时也可以指 $AVL$ 树（第一棵平衡二叉搜索树），而其他平衡二叉树则有独有名字。这里按照 $ALV$ 树对平衡二叉搜索树进行解释。

*AVL 树**：一棵自平衡的二叉搜索树。树中每个节点的右子树高度 - 左子树高度的绝对值不超过 $1$ 。
所谓自平衡，即每次树的结构因插入或删除导致改编后，树的高度会自动平衡在 $O(\log n)$ 。

由 AVL 树的定义，显然 AV$ 树的子树也是 AVL 树。

平衡因子：
AVL 树的每个节点维护了一个平衡因子 $\alpha$ ：左子树高度 $h_l$ - 右子树高度 $h_r$ ，且可以保证 $|\alpha| \leq 1$ 。

如果平衡因子可以被维护，则是可以证明 AVL 树的树高是 $O(\log n)$ 的。
证明：
若高度 $h$ 是节点数为 $n$ 的 AVL 树的最低高度，则 $n$ 是高度 $h$ 的 AVL 树的最少节点数，设 $n = f_{h}$ ，有
若 $h = 0$ ，显然 $f_{h} = 0$ ；
若 $h = 1$ ，显然 $f_{h} = 1$ ；
若 $h = 2$ ，显然 $f_{h} = 2$ ；
若 $h > 2$ ，则高度为 $h$ 的子树存在一棵子树高度为 $n - 1$ ，另一颗子树高度为 $h - 1$ 或 $h - 2$ 。当前子树的最少节点 = 左子树的最少节点 + 右子树的最少节点 + 1 。
对于一棵高度为 $h - 1$ 且有 $f_{h - 1}$ 个节点的树，剪去最后一层的节点得到一棵高度为 $h - 2$ 的树，故 $f_{h - 2} \leq f_{h - 1}$ 。继而 $f_{h} = f_{h - 1} + f_{h - 2} + 1$ 。
于是有 $f_{h} = f_{h - 1} + f_{h - 2} + 1, h \geq 2, f_{0} = 0$ 。构造 $f_{h}$ 的递推矩阵并解特征方程（这里有一套标准的 dirty work）得到

\[\begin{aligned} f_{h} &= \frac{5 + 2\sqrt{5}}{5} \phi^{h-1} + \frac{5 - 2\sqrt{5}}{5} \psi^{h-1} - 1 \ s.t. \ \phi = \frac{1 + \sqrt{5}}{2}, \quad \psi = \frac{1 - \sqrt{5}}{2} \\ f_{h} &= \left [ \frac{5 + 2\sqrt{5}}{5} \phi^{h-1} \right ] - 1 \end{aligned} \]

于是

\[h \sim \log_{\phi} (f_{h} + 1) + 1 \ s.t. \ \phi = \frac{1 + \sqrt{5}}{2}, \ f_{h} = n \implies h = O(\log n) \]

$\square$

继而考虑如何维护平衡因子 $\alpha$ ，显然只有插入和删除操作改变树结构，需要维护平衡因子 $\alpha$。
进一步分析，平衡因子 $\alpha$ 若被破坏，则一定是左子树或右子树的高度 $\pm 1$ ，进而导致平衡因子从 $|\alpha| = 1$ 变成了 $|\alpha| = 2$ 。

不妨设 $\alpha = h_{l} - h_{r} = 2$ ，否则我们可以对称地考虑

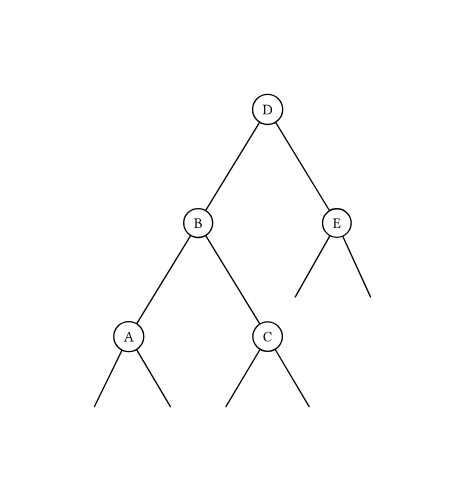
设 $h_c = x$ ，则 $h_l = x - 1, h_l = x - 3$ 。
case 1 ：

\[\frac{az - m}{a - b} \leq x \leq \frac{n - bz}{a - b} \]

posted @ 2025-12-23 13:14 03Goose 阅读(6) 评论(0) 收藏举报

刷新页面返回顶部

从“树”到“平衡二叉搜索树”

公告