【图论】差分约束

求一个形如 \(a_i \leq b_i + c_i (1 \leq i \leq n)\) 不等式组的一组最值解。

考虑图论做法：对于每个不等式 \(a_i \leq b_i + c_i\)，连接边 \((b_i, a_i, c_i)\)（有向边，权值为 \(c\)）。每个不等式都对应了一条边，这个不等式组就可以生成出一张表示变量之间逻辑关系的图。例如，它对应的图就是这样：

\[\begin{cases} a - b \geq -1 \\ c - b \leq 3 \\ d \leq c - 2 \\ e + 1 \leq c \\ e - b \geq 4 \end{cases} \Longrightarrow \begin{cases} b \leq a + 1 \\ c \leq b + 3 \\ d \leq c - 2 \\ e \leq c - 1 \\ b \leq e - 4 \end{cases} \]

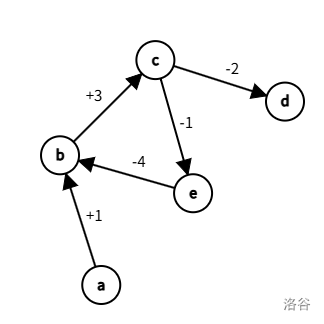
设点 \(k_u\) 为变量 \(u\) 的最大值。对于边 \((u, v)\) 有 \(k_v = k_u + w_{(u, v)}\)。在一条路径上迭代计算 \(k_u\) 的过程，就相当于是合并了从起点到终点之间的所有不等式，它的解集同时被包含于两点之间的每个不等式的解集中，它的最大解就可以满足这条路径上所有的不等式。所以根据点 \(u\) 的可行取值，所有它能够到达的点的最大值就都是可求的。那么，若想求 \(u\) 同时满足所有不等式的最大解，就需要联立每一条以它为结尾的路径所合并出的不等式，并取最小值。这难以办到，毕竟我们并不知道这样的路径有什么。但是可以创造一个虚拟源点，向所有点连一条权为 \(0\) 的边。这就保证了图是联通的，仅需求一次以它为源的单源最短路，就相当于尝试了以每一点为起点的路径，若能到达 \(u\)，就会被计入答案。

当然，是不等式组就会存在无解的情况，那又要怎么处理呢？实际也很简单，因为负环会导致最短路出现问题，所以它的出现就代表着无解。从数学上是可以证明的。设环有节点 \(x_1, \dots x_n\)：

\[\begin{aligned} & k_{x_2} = x_1 + w_{(x_1, x_2)} \\ & \Rightarrow k_{x_3} = k_{x_2} + w_{(x_2, x_3)} \\ & \Rightarrow \cdots \cdots \\ & \Rightarrow k_{x_1} = k_{x_{n}} + w_{(x_{n}, x_1)} \\ & \therefore k_{x_1} = x_1 + \Sigma w \\ & \therefore x_1 \leq x_1 + \Sigma w \end{aligned} \]

这个不等式显然无解，产生矛盾，原不等式组无解。

同时给每个变量加上一个相同的数，不等式组仍然成立。所以，虚拟源点的 \(k\) 值，可以任意取一个值。

注意：由于不等式的形式问题，按上文那样操作，我们只能求出变量的最大值。若要求最小值，必须变成 \(a_i \geq b_i + c_i\) 的形式，并且求最长路（同时满足 \(u, v\) 间所有路径合并得到的不等式，由于是大于等于，需要取大的，即为最长路）；无解判断方面，负环也要改成正权环（求最短路，如果存在负环，\(k\) 会被更新至无穷小，就会导致求不出来解，反之如果是正权环，就是无穷大）。由于有环的判断，只能用 SPFA 求解。