机器学习基石笔记6——为什么机器可以学习(2)
转载请注明出处:http://www.cnblogs.com/ymingjingr/p/4271742.html
目录
机器学习基石笔记1——在何时可以使用机器学习(1)
机器学习基石笔记2——在何时可以使用机器学习(2)
机器学习基石笔记3——在何时可以使用机器学习(3)(修改版)
机器学习基石笔记4——在何时可以使用机器学习(4)
机器学习基石笔记5——为什么机器可以学习(1)
机器学习基石笔记6——为什么机器可以学习(2)
机器学习基石笔记7——为什么机器可以学习(3)
机器学习基石笔记8——为什么机器可以学习(4)
机器学习基石笔记9——机器可以怎样学习(1)
机器学习基石笔记10——机器可以怎样学习(2)
机器学习基石笔记11——机器可以怎样学习(3)
机器学习基石笔记12——机器可以怎样学习(4)
机器学习基石笔记13——机器可以怎样学得更好(1)
机器学习基石笔记14——机器可以怎样学得更好(2)
机器学习基石笔记15——机器可以怎样学得更好(3)
机器学习基石笔记16——机器可以怎样学得更好(4)
六、Theory of Generalization
泛化理论(举一反三)。
6.1 Restriction of Break Point
突破点的限制。
回顾一下上一章中提到的成长函数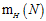 的定义:假设空间在N个样本点上能产生的最大二分(dichotomy)数量,其中二分是样本点在二元分类情况下的排列组合。
的定义:假设空间在N个样本点上能产生的最大二分(dichotomy)数量,其中二分是样本点在二元分类情况下的排列组合。
上一章还介绍了突破点(break point)的概念,即不能满足完全分类情形的样本点个数,完全二分类情形(shattered)是可分出 种二分类(dichotomy)的情形。
种二分类(dichotomy)的情形。
继续举例说明,假设一种分类情形最小的突破点为2,即 。
。
容易求出在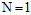 时,成长函数
时,成长函数 ;
;
在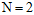 时,成长函数
时,成长函数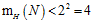 (突破点是2),因此最大的二分类个数不可能超过3,假设为3。
(突破点是2),因此最大的二分类个数不可能超过3,假设为3。
继续观察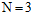 时的情形,因理解稍微有些复杂,还是以图的形式表达,如图6-1所示。
时的情形,因理解稍微有些复杂,还是以图的形式表达,如图6-1所示。
如图6-1a)表示在三个样本点时随意选择一种二分的情况,这种分类没有任何问题,不会违反任意两个样本点出现四种不同的二分类情况(因为突破点是2);
如图6-1b)表示在a)的基础上,添加不与之前重复的一种二分类,出现了两种不冲突的二分类,此时同样也没有任何问题,不会违反任意两个样本点出现四种不同的二分类情况;
如图6-1c) 表示在b)的基础上,再添加不与之前重复的一种二分类,出现了三种不冲突的二分类,此时同样也没有任何问题,不会违反任意两个样本点出现四种不同的二分类情况;
如图6-1d) 表示在c)的基础上,再添加不与之前重复的一种二分类,问题出现了,样本 出现了四种不同的二分情况,和已知条件中k=2矛盾(最多只能出现三种二分类),因此将其删去。
出现了四种不同的二分情况,和已知条件中k=2矛盾(最多只能出现三种二分类),因此将其删去。
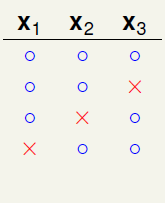
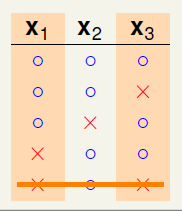
如图6-1e) 表示在c)的基础上,再添加不与之前重复的一种二分类,此时同样也没有任何问题,不会违反任意两个样本点出现四种不同的二分类情况;
如图6-1f) 表示在e)的基础上,再添加不与之前重复的一种二分类,问题又出现了,样本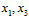 出现了四种不同的二分情况,和已知条件中k=2的条件不符(最多只能出现三种二分类),因此将其删去。
出现了四种不同的二分情况,和已知条件中k=2的条件不符(最多只能出现三种二分类),因此将其删去。
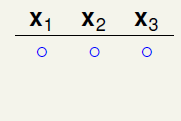

a) b)


c) d)
e) f)
图6-1 样本数为3时的二分类情形
在突破点是2,样本点为3时,最多只能有四种二分类情况,而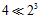 。
。
从上述情形,可以做一个猜想,成长函数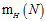 小于等于某个与突破点k有关的二次项,如果可以证明这一结论,即能寻找到一个可以取代无限大M的数值,同理即能公式4-6在假设空间为无限大时也是成立,即机器是可以学习的。
小于等于某个与突破点k有关的二次项,如果可以证明这一结论,即能寻找到一个可以取代无限大M的数值,同理即能公式4-6在假设空间为无限大时也是成立,即机器是可以学习的。
假设突破点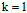 ,在样本数为3时,最大的二分类个数是多少?答案是1,可以想象,在样本为1时,只有一种分类情形,假设这种情形是正,则以后所有样本也为正,才能满足上述条件,所以样本N不论为多少,其最大二分类数都是1。
,在样本数为3时,最大的二分类个数是多少?答案是1,可以想象,在样本为1时,只有一种分类情形,假设这种情形是正,则以后所有样本也为正,才能满足上述条件,所以样本N不论为多少,其最大二分类数都是1。
6.2 Bounding Function- Basic Cases
上限函数的基本情形。
根据上一小节的例子,提出一个新的概念,上限函数 (bounding function),其定义为在最小突破点为k时,表示成长函数
(bounding function),其定义为在最小突破点为k时,表示成长函数 最大值的函数。此函数将成长函数从各种假设空间的关系中解放出来,不用再去关心具体的假设,只需了解此假设的突破点,突破点相同的假设视为一类,抽象化成长函数与假设的关系。
最大值的函数。此函数将成长函数从各种假设空间的关系中解放出来,不用再去关心具体的假设,只需了解此假设的突破点,突破点相同的假设视为一类,抽象化成长函数与假设的关系。
二分类的个数或者称之为成长函数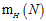 说白了就是二元(在图中表示为"×"或者"○ "的符号)符号在在长度为N的情况下的排列组合(每个不同的排列代表一个二分类,每种二分类可看做一个向量)个数。
说白了就是二元(在图中表示为"×"或者"○ "的符号)符号在在长度为N的情况下的排列组合(每个不同的排列代表一个二分类,每种二分类可看做一个向量)个数。
在强调一遍,提出这种上限函数的好处在于,它的性质可以不用关心到底使用的是何种假设空间,只需要知道突破点便可以得到一个上限函数来对成长函数做约束。
例如: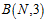 可以同时表示一维空间的感知器(1D perceptrons)和间隔为正(positive intervals)的两种假设空间,因为两者都满足
可以同时表示一维空间的感知器(1D perceptrons)和间隔为正(positive intervals)的两种假设空间,因为两者都满足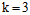 。注意一维的成长函数为
。注意一维的成长函数为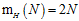 ,而间隔为正的成长函数为
,而间隔为正的成长函数为 ,
,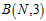 一定比这两种情况中最大的还要大,才能约束成长函数,回忆上限函数的定义,是成长函数
一定比这两种情况中最大的还要大,才能约束成长函数,回忆上限函数的定义,是成长函数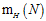 最大值的函数表示,从这个例子中可以理解为何还会出现"最大值"。
最大值的函数表示,从这个例子中可以理解为何还会出现"最大值"。
想要证明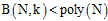 。
。
先观察已知的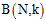 如何表示,通过列表方式找出规律,如图6-2所示。
如何表示,通过列表方式找出规律,如图6-2所示。
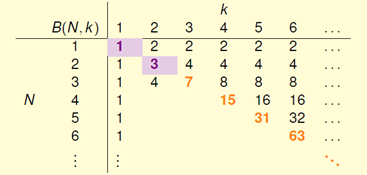
图6-2 已知的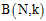 取值
取值
在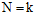 的这条斜线上,所有值都等于
的这条斜线上,所有值都等于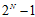 ,这一原因在上一节推导中已经提到过,原因是突破点代表不能完全二分类
,这一原因在上一节推导中已经提到过,原因是突破点代表不能完全二分类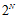 的情况,因此在此情况下最大的二分类数可以是
的情况,因此在此情况下最大的二分类数可以是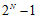 。在这条斜线的右上角区域所有的点都满足完全二分类的,因此值为
。在这条斜线的右上角区域所有的点都满足完全二分类的,因此值为 。
。
而在斜线右下角上已给出数值的点都是在上一节中已求出答案的点,空白地方的值则是下节需要介绍的内容。
6.3 Bounding Function- Inductive Cases
上限函数的归纳情形。
这一小节主要是将上一小节空白的内容填写上,从已有的数据上可以看出一个似乎是正确的结论:每个值等于它正上方与左上方的值相加。如公式6-1所示。
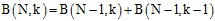 (公式6-1)
(公式6-1)
当然单从观察是无法证明该公式是成立的,以下从结论出发来验证它的正确性。
首先通过计算机求出 的所有二分情况(自己编写程序加上限制条件,在16个二分类中找出符合条件的),其结果如图6-3所示。
的所有二分情况(自己编写程序加上限制条件,在16个二分类中找出符合条件的),其结果如图6-3所示。

图6-3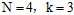 的所有二分类
的所有二分类
图6-3中的展示效果还是有些混乱,对这11种情况做一次重新排序,将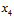 与
与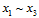 分开观察,如图6-4所示,橙色部分为
分开观察,如图6-4所示,橙色部分为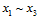 两两一致、
两两一致、 成对(pair)出现的二分类,设橙色部分一共
成对(pair)出现的二分类,设橙色部分一共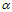 对二分类,即
对二分类,即 种二分类;紫色部分为各不相同的
种二分类;紫色部分为各不相同的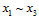 ,设紫色部分一共
,设紫色部分一共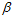 种,得公式6-2。
种,得公式6-2。
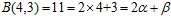 (公式6-2)
(公式6-2)

图6-4 以成对和单个的形式展示
注意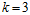 ,意味着在样本点为3时,不能满足完全二分的情形。需要观察在样本数为3时,这11种分类会有何变化,不妨假设这三个样本是
,意味着在样本点为3时,不能满足完全二分的情形。需要观察在样本数为3时,这11种分类会有何变化,不妨假设这三个样本是 ,于是只剩如图6-5所示的7种二分类情形。
,于是只剩如图6-5所示的7种二分类情形。

图6-5 三个样本时缩减之后的二分类
其中橙色部分,原本两两成对出现的二分类,在去掉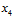 所属的那列样本之后,就合并成了4种二分类情况(
所属的那列样本之后,就合并成了4种二分类情况( ),紫色部分不变依然为3种二分情况(
),紫色部分不变依然为3种二分情况( )。因为已知
)。因为已知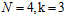 ,在样本数为3时,图6-5中即表示样本书为3 的情况,其一定不能满足完全二分,因此
,在样本数为3时,图6-5中即表示样本书为3 的情况,其一定不能满足完全二分,因此 与
与 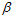 一定满足公式6-3。
一定满足公式6-3。
 (公式6-3)
(公式6-3)
继续观察橙色部分的区域,如图6-6所示。
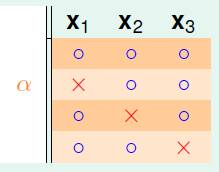
图6-6 三个样本时橙色区域的二分类
以下使用反证法证明。假设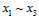 三个样本在如上图所示的四种二分类情况下,满足任意两个样本都可完全二分类。将
三个样本在如上图所示的四种二分类情况下,满足任意两个样本都可完全二分类。将 中任意两列取出,同之前被删除的
中任意两列取出,同之前被删除的 列相结合,一定可得到一种三个样本都满足完全二分类的情形(因为不论是哪两列与
列相结合,一定可得到一种三个样本都满足完全二分类的情形(因为不论是哪两列与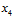 相结合都会得到8种二分类,每一行二分类都对应两个不同标记的
相结合都会得到8种二分类,每一行二分类都对应两个不同标记的 ,因此为8种。且两列四行的二分类是全完二分的,在此基础上加上不同属性的列,应该也不会重复,因此一定也是全完二分的)。但是此结论和已知任意三个样本不能完全二分冲突了,因此假设不成立,即在图6-6中一定存在某两个样本点不能完全二分的情况,因此得出如公式6-4所示的结论。
,因此为8种。且两列四行的二分类是全完二分的,在此基础上加上不同属性的列,应该也不会重复,因此一定也是全完二分的)。但是此结论和已知任意三个样本不能完全二分冲突了,因此假设不成立,即在图6-6中一定存在某两个样本点不能完全二分的情况,因此得出如公式6-4所示的结论。
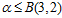 (公式6-4)
(公式6-4)
由公式6-2~公式6-4推导出公式6-5。
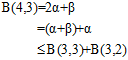 (公式6-5)
(公式6-5)
最终还能推导出公式6-6的通用结论,也就是开始时公式6-1的猜想。
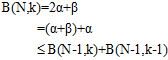 (公式6-6)
(公式6-6)
根据这一结论将图6-2补齐,如图6-7所示。
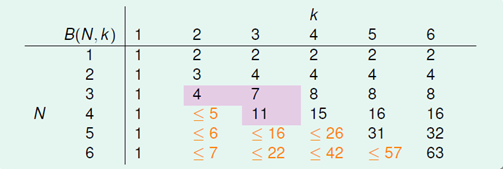
图6-7 补齐后的上限函数表
最后可以通过如下方式证明公式6-7是成立的。
 (公式6-7)
(公式6-7)
首先需要预先了解组合中的一个定理,如公式6-8所示。
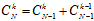 (公式6-8)
(公式6-8)
很容易证明 情况下公式6-7成立,如公式6-9所示。
情况下公式6-7成立,如公式6-9所示。
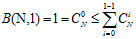 (公式6-9)
(公式6-9)
上一节中已经给出了证明,不仅仅是满足不等号条件,而且满足等号。
再使用数学归纳法证明在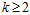 的情况,公式6-7成立。
的情况,公式6-7成立。
假设公式6-10成立,则可以得到在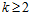 的情况下公式6-11成立,同时结合公式6-6的结论,公式6-12也能被推导出来。
的情况下公式6-11成立,同时结合公式6-6的结论,公式6-12也能被推导出来。
 (公式6-10)
(公式6-10)
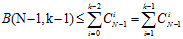 (公式6-11)
(公式6-11)
 (公式6-12)
(公式6-12)
这一结果意味着:成长函数 的上限函数
的上限函数 的上限为
的上限为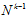 。
。
6.4 A Pictorial Proof
一种形象化的证明。
在书写这一小节之前,还是想说明一下,我面对这一小节时,看得是一知半解,因为林老师本身也没打算将这个证明的详细流程全部给出,我觉得原因有几个:一是难度很高,即使全部讲解能听懂的估计也没几个;二是思想更重要,你只需要知道它用到了什么原理去证明这个问题,这比你了解这枯燥的数学推导更重要;三是结论比求解过程更重要。当然这不是说求解过程不重要,我会在看懂相关理论之后,整理出一个关于V-C限制完整证明的笔记,但估计现在也没时间去看懂这一理论。
言归正传,开始这一小节的简单阐述。
在讲述之前几章时,一直以为只需要证明出在假设函数为无限多的情况下,寻找成长函数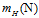 作为假设空间个数的上限,直接使用该上限去取代原本霍夫丁不等式中的M便可得出结论,即在
作为假设空间个数的上限,直接使用该上限去取代原本霍夫丁不等式中的M便可得出结论,即在 接近0时,
接近0时, 也接近0,也就是机器是可以学习的。实际与这一结果类似,但是稍有偏差,在那本以为的霍夫丁不等式(如公式6-13所示)的公式中多出一些常量。
也接近0,也就是机器是可以学习的。实际与这一结果类似,但是稍有偏差,在那本以为的霍夫丁不等式(如公式6-13所示)的公式中多出一些常量。
 (公式6-13)
(公式6-13)
先给出结论,公式如6 -14所示。
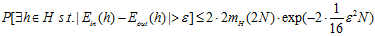 (公式6-14)
(公式6-14)
比较两个公式,发现最终的结论比猜想的,在不等式的右侧三个不同位置多了三个常数,分别是开头的地方多了一个2倍,成长函数中多了一个2倍,指数函数中多了一个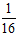 。按先后循序,分三步简单说明一下这些变化的原因。
。按先后循序,分三步简单说明一下这些变化的原因。
第一步,用 取代
取代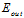 。
。
公式6-15的说明(不敢叫做证明,目前完全没有头绪,一到三步的说明都是自己的理解,不正确之处还望指正)。
 (公式6-15)
(公式6-15)
其中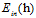 的可能性是有限多种,因为假设空间的种类被成长函数
的可能性是有限多种,因为假设空间的种类被成长函数 约束住了,而样本的大小又是固定的,所以错误率也最多只有
约束住了,而样本的大小又是固定的,所以错误率也最多只有 种;但是
种;但是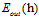 的可能性还是无限多,因为它的数据是无限大,错误率也自然也会无限多种。为了解决此问题,提出了一种叫做影子数据的概念(ghost data)。使用跟输入样本一样多的数据
的可能性还是无限多,因为它的数据是无限大,错误率也自然也会无限多种。为了解决此问题,提出了一种叫做影子数据的概念(ghost data)。使用跟输入样本一样多的数据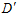 ,有
,有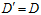 ,用这组新的样本取代整个样本去近似求解在无限大的数据中
,用这组新的样本取代整个样本去近似求解在无限大的数据中 的值,求解的近似值记为
的值,求解的近似值记为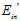 。图6-8表示
。图6-8表示 和
和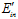 的分布情况,其中
的分布情况,其中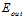 为它俩的分布中心,假设数据D的情况下
为它俩的分布中心,假设数据D的情况下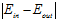 很大,从图中不难看出,再抽取一次数据
很大,从图中不难看出,再抽取一次数据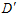 得到的
得到的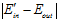 很大的几率,最多只有条件
很大的几率,最多只有条件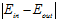 很大的一半概率,意味着
很大的一半概率,意味着 和
和 很接近的几率最多只有
很接近的几率最多只有 很大这个条件的一半(因为从该图中得知
很大这个条件的一半(因为从该图中得知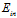 和
和 只可能变得小于
只可能变得小于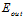 ),即
),即 很小的几率最多只有
很小的几率最多只有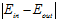 很大这一几率的一半。换句话说
很大这一几率的一半。换句话说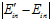 很大的几率至少是
很大的几率至少是 很大这一几率的一半,用公式6-16表示其含义如下:
很大这一几率的一半,用公式6-16表示其含义如下:
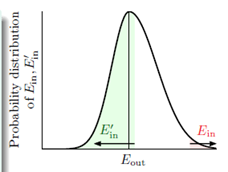
图6-8 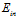 和
和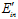 的分布
的分布
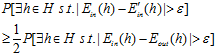 (公式6-16)
(公式6-16)
将公式6-16稍微调整一下就可以得到公式6-17。
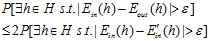 (公式6-17)
(公式6-17)
从公式6-17到公式6-15多了一个更强的约束,因此从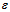 变成了
变成了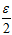 。
。
第二步,分解假设空间的种类
其中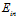 的可能性与样本D有关,而
的可能性与样本D有关,而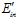 与样本
与样本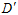 有关,因此整个假设空间的种类可以写成
有关,因此整个假设空间的种类可以写成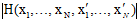 的个数,我们又从之前几章的内容得知,种类的个数并非无限多,其上限最大为成长函数
的个数,我们又从之前几章的内容得知,种类的个数并非无限多,其上限最大为成长函数 那,因此坏事情发生的概率如公式6-18所示。
那,因此坏事情发生的概率如公式6-18所示。
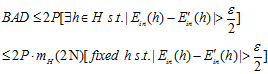 (公式6-18)
(公式6-18)
第三步,使用无取回的霍夫丁。
还是用小球和罐子的那个例子解释,罐子中不再是无限多个小球,而是2N个小球,选择N个小球而留下另外N个,可以通过公式6-19得出如下结论。
 (公式6-19)
(公式6-19)
这是一种无放回的霍夫丁,最终得到公式6-20。
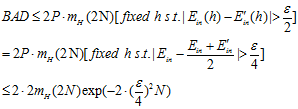 (公式6-20)
(公式6-20)
至此说明了(不敢叫证明)一个在机器学习领域很著名的理论——V-C上界制(Vapnik-Chervonenkis bound)。
2维的感知器,其突破点为4,因此其成长函数为 ,可以使用这个VC上界来说明在样本N足够大时候,发生坏事的情况很少,即选择一个在样本中错误率很小的g,可以得出其在整个数据上错误率也很低的结论,说明机器学习是可能的。
,可以使用这个VC上界来说明在样本N足够大时候,发生坏事的情况很少,即选择一个在样本中错误率很小的g,可以得出其在整个数据上错误率也很低的结论,说明机器学习是可能的。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号