机器学习基石笔记12——机器可以怎样学习(4)
转载请注明出处:http://www.cnblogs.com/ymingjingr/p/4271742.html
目录
机器学习基石笔记1——在何时可以使用机器学习(1)
机器学习基石笔记2——在何时可以使用机器学习(2)
机器学习基石笔记3——在何时可以使用机器学习(3)(修改版)
机器学习基石笔记4——在何时可以使用机器学习(4)
机器学习基石笔记5——为什么机器可以学习(1)
机器学习基石笔记6——为什么机器可以学习(2)
机器学习基石笔记7——为什么机器可以学习(3)
机器学习基石笔记8——为什么机器可以学习(4)
机器学习基石笔记9——机器可以怎样学习(1)
机器学习基石笔记10——机器可以怎样学习(2)
机器学习基石笔记11——机器可以怎样学习(3)
机器学习基石笔记12——机器可以怎样学习(4)
机器学习基石笔记13——机器可以怎样学得更好(1)
机器学习基石笔记14——机器可以怎样学得更好(2)
机器学习基石笔记15——机器可以怎样学得更好(3)
机器学习基石笔记16——机器可以怎样学得更好(4)
十二、Nonlinear Transformation
非线性转换。
12.1 Quadratic Hypotheses
二次的假设空间。
在之前的章节中,学习的机器学习模型都为线性模型,即假设空间都为线性的,使用的得分为线性得分(linear scores)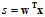 。这种线性模型的最大好处是理论上可以使用VC限制进行约束(假设是非线性的各种曲线或者超曲面,则每种假设都可以完全二分,即
。这种线性模型的最大好处是理论上可以使用VC限制进行约束(假设是非线性的各种曲线或者超曲面,则每种假设都可以完全二分,即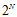 种二分类),这保证了
种二分类),这保证了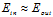 ;当遇到如图12-1的情况,则很难寻找到一个直线能将两类尽可能的分离,即存在很大的
;当遇到如图12-1的情况,则很难寻找到一个直线能将两类尽可能的分离,即存在很大的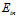 。该如何打破这种限制?
。该如何打破这种限制?
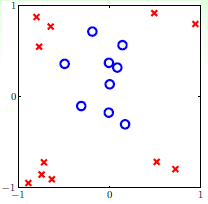
图12-1 线性不可分的情况
观察图12-1发现该数据集为线性不可分(non-linear separable)的情况,可以使用圆圈将样本集分离,如图12-2所示,此种方式称作圆圈可分(circular separable),该图使用一个半径为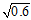 圆心在原点的圆划分,假设函数h如公式12-2所示,该公式的含义为将样本点到原点距离的平方与数值0.6作比较,如果比0.6小,则标记为+1;反之为-1。
圆心在原点的圆划分,假设函数h如公式12-2所示,该公式的含义为将样本点到原点距离的平方与数值0.6作比较,如果比0.6小,则标记为+1;反之为-1。
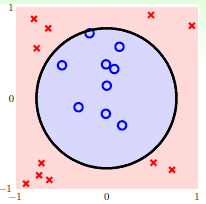
图12-2 圆圈可分的情况
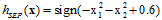 (公式12-1)
(公式12-1)
难道需要再将以前学过的线性PLA,线性回归的算法都重新设计一遍,变成圆圈PLA,圆圈回归重新学习?当然不会这样,以下介绍一种思想通过已有知识解决上述新提出的算法模型。
将公式12-1中变量以及参数做一些转变,变成熟悉的线性模型,如公式12-2所示。
 (公式12-2)
(公式12-2)
该公式将圆圈可分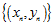 转换成线性可分
转换成线性可分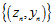 ,得到的结果如图12-3所示。称这种将输入空间
,得到的结果如图12-3所示。称这种将输入空间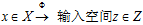 的过程称为特征转换(feature transform
的过程称为特征转换(feature transform 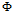 )。
)。
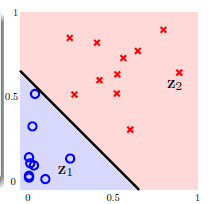
图12-3 在Z空间线性可分的情况
问题出现了,是否新的空间中数据线性可分,则在原空间中原数据一定是圆圈可分?搞清此问题之前,需要了解在新的空间中如何线性可分的。
新的空间Z的表示如公式12-3所示。
 (公式12-3)
(公式12-3)
在空间X中假设函数h与空间Z假设函数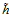 的关系如公式12-4所示。
的关系如公式12-4所示。
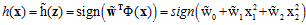 (公式12-4)
(公式12-4)
公式12-4即为在X空间中假设函数的表达式,其中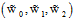 为权值向量,观察权值向量的不同取值对X空间的中的假设函数的表达式有何不同,如表12-1所示。
为权值向量,观察权值向量的不同取值对X空间的中的假设函数的表达式有何不同,如表12-1所示。
表12-4 Z空间不同权值向量对应X空间的不同假设函数
|
Z空间的权值向量 |
X空间的假设函数 |
图形 |
|
|
|
圆形(circle) |
|
|
|
椭圆形(ellipse) |
|
|
|
抛物线(hyperbola) |
|
|
|
全为+1 |
因此通过这种形式转换的Z空间的直线对应着原X空间中特殊的二次曲线(quadratic curves)。为何说是特殊的?从表12-1第一行表示的圆只能是圆心过原点的圆,不能随意表示各种情况的圆。
如果想要表示X空间中所有的二次曲面,Z空间该佮表示呢?设计一个更大的Z空间,其特征转换如公式12-5所示。
 (公式12-5)
(公式12-5)
通过以上特征转换,Z空间中的每个超平面就对应X空间中各种不同情况的二次曲线。则X空间中的假设空间H如公式12-6所示。
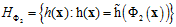 (公式12-6)
(公式12-6)
其中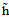 表示Z空间中的假设函数。使用一个例子表示,如公式12-7为斜椭圆的表达式,可以得出权值向量
表示Z空间中的假设函数。使用一个例子表示,如公式12-7为斜椭圆的表达式,可以得出权值向量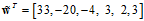 。
。
 (公式12-7)
(公式12-7)
使用公式12-5的特征转换,可以表示X空间中所有的线(包括直线和各种类型的二次曲线)和常数(全为正或全为负)。
12.2 Nonlinear Transform
非线性转换。
从X空间转换到Z空间,则在Z空间中获得的好的线性假设函数,相当于在X空间中获得了好的二次假设函数,即在Z空间中存在一个可分的直线对应于在X空间存在一个可分的二次曲线。如何在Z空间中寻找好的假设函数呢?
将在Z空间的数据集写成如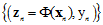 ,前面的章节讲述了如何在X空间的数据集
,前面的章节讲述了如何在X空间的数据集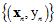 中寻找最好的假设函数,因此可以使用前面章节学习到的方法对Z空间的数据集进行训练。
中寻找最好的假设函数,因此可以使用前面章节学习到的方法对Z空间的数据集进行训练。
简述下此种学习方式的步骤,转换与学习步骤如图12-4所示:
通过特征转换函数 将在X空间中不可分的数据集
将在X空间中不可分的数据集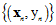 转换成在Z空间中可分的数据集
转换成在Z空间中可分的数据集 ;
;
使用线性分类算法通过数据集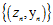 获得寻找最优权值向量
获得寻找最优权值向量 ;
;
返回假设函数g, 。
。
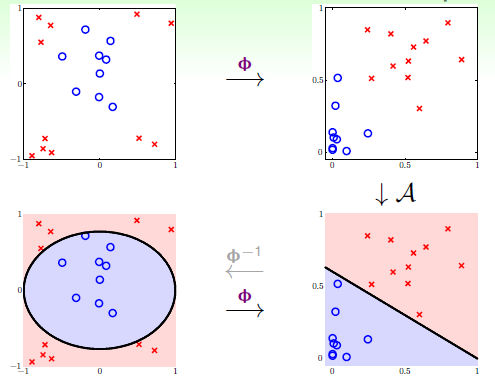
图12-4 非线性的转换步骤
判断一个新的样本点是属于哪一类,只需要如图12-4最下面两幅,从左到右做转换,即将X空间中的数据点转换为Z空间中的一个数据点,使用Z空间中的假设函数,最终判断该样本点在X空间中的类别。
总结起来此种非线性模型算法为非线性转换结合线性算法实现,因此包含两个重要的特征:转换函数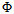 和线性模型(线性模型包括前几章中讨论的二元分类、线性回归和logistic回归等等)。
和线性模型(线性模型包括前几章中讨论的二元分类、线性回归和logistic回归等等)。
以上求解非线性分类的思路不仅可以解决二次分类的问题,同时也可以用在三次感知器、三次回归,甚至多项式回归的问题上。
特征转换是机器学习中一个非常重要的知识点。
12.3 Price of Nonlinear Transform
非线性转换的代价。
当使用Q次多项式转换时,转换函数如公式12-8所示。
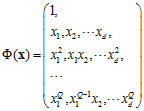 (公式12-8)
(公式12-8)
此时权值向量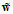 的维度是多少?答案为
的维度是多少?答案为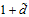 ,其中1为
,其中1为 ,
,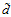 表示转换后特征对应的权值分量个数。
表示转换后特征对应的权值分量个数。
如何计算维度?需要使用到排列组中重复组合的知识,从n个不同元素中无序可重复的抽取k个元素,用隔板法可知为 (证明思路就是在n个小球中插入k-1个板子,这种组合方式为
(证明思路就是在n个小球中插入k-1个板子,这种组合方式为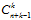 ),用在求解
),用在求解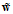 的维度时,要注意除了给定的元素
的维度时,要注意除了给定的元素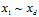 之外,还有一个元素为常数1,因此该问题为在d+1个元素中可重复的抽出Q个元素,维度为
之外,还有一个元素为常数1,因此该问题为在d+1个元素中可重复的抽出Q个元素,维度为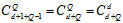 ,可表示为
,可表示为 。因此不论是对空间转换或权值向量
。因此不论是对空间转换或权值向量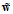 计算与存储上都消耗了更高时间复杂度和空间复杂度。因此在Q很大时,模型的计算非常困难。
计算与存储上都消耗了更高时间复杂度和空间复杂度。因此在Q很大时,模型的计算非常困难。
除上述的弊端之外,特征转换还带来另一个问题。
在前面的章节中讲述过,模型参数的自由度大概是该模型的VC维度,如公式12-9所示。
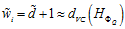 (公式12-9)
(公式12-9)
因此当Q越大时, 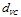 越大。
越大。
还记得第七章的表7-1的总结吗?此处使用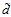 取代近似的
取代近似的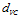 ,得到表12-2。
,得到表12-2。
表12-2 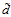 的大小与两个条件的关系
的大小与两个条件的关系
|
|
|
|
|
第一个问题 |
满足, 不好情况出现的几率变小 |
不满足, 不好情况出现的几率变大了 |
|
第二个问题 |
不满足,在 |
满足,在 |
问题一是如何确保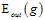 与
与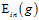 很接近;问题二是如何确保
很接近;问题二是如何确保 足够小。
足够小。
如果表12-2还不够形象,在举一个形象化的例子,如图12-5所示,图12-5 a)表示使用原始的线性函数,图12-5 b)表示4次函数的划分,视觉上可以看出图12-5 b)的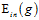 虽小,但是划分有些过了,可能和
虽小,但是划分有些过了,可能和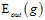 差得很远。
差得很远。
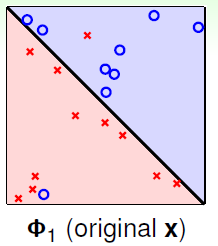
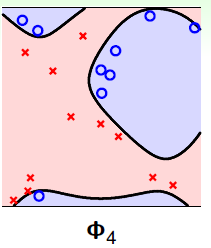
图12-5 a) 原始的1次函数分类情况 b) 4次函数的分类情况
但是这种"视觉上"判断的好坏已经是人类的大脑处理过后的结果,在机器学习中应避免直接观察数据的情况出现。
12.4 Structured Hypothesis Sets
结构化的假设空间。
观察不同维度间假设空间、VC维及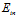 的关系,如公式12-10~公式12-12。
的关系,如公式12-10~公式12-12。
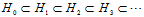 (公式12-10)
(公式12-10)
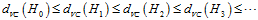 (公式12-11)
(公式12-11)
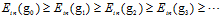 (公式12-12)
(公式12-12)
其中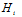 ,
, ,表示i次多项式转换的假设空间,公式12-10表示高次多项式转换的假设空间包含了低次多项式转换的假设空间;公式12-11表示高次多项式转换的VC维度大于等于低次多项式转换的VC维度;次数越高所能表示的边界越复杂,
,表示i次多项式转换的假设空间,公式12-10表示高次多项式转换的假设空间包含了低次多项式转换的假设空间;公式12-11表示高次多项式转换的VC维度大于等于低次多项式转换的VC维度;次数越高所能表示的边界越复杂,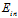 自然越小。
自然越小。
VC维与错误率之间的关系如图12-6所示。
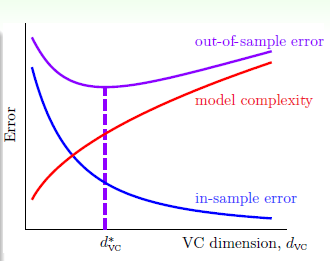
图12-6 VC维与错误率之间的关系
从图中可以得知,如果开始选择一个高次多项式转换,则可能得到的 非常小,然而此种情况对应的
非常小,然而此种情况对应的 或许非常大。因此在做多项式转换时,最好是从低次往高次依次测试,而不是开始选取一个高次的多项式作为转换函数,最好从一次式(也称为线性函数)开始。
或许非常大。因此在做多项式转换时,最好是从低次往高次依次测试,而不是开始选取一个高次的多项式作为转换函数,最好从一次式(也称为线性函数)开始。


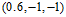
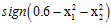
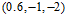


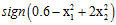
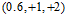
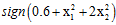
 很小的时候
很小的时候 很大的时候
很大的时候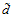 变小时,假设的数量变小,算法的选择变小,可能无法找到
变小时,假设的数量变小,算法的选择变小,可能无法找到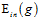 接近0的假设。
接近0的假设。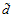 变大时,假设的数量变大,算法的选择变大,找到
变大时,假设的数量变大,算法的选择变大,找到 接近0的假设的几率变大。
接近0的假设的几率变大。
 浙公网安备 33010602011771号
浙公网安备 33010602011771号