数据结构基础温故-4.树与二叉树（下）

上面两篇我们了解了树的基本概念以及二叉树的遍历算法，还对二叉查找树进行了模拟实现。数学表达式求值是程序设计语言编译中的一个基本问题，表达式求值是栈应用的一个典型案例，表达式分为前缀、中缀和后缀三种形式。这里，我们通过一个四则运算的应用场景，借助二叉树来帮助求解表达式的值。首先，将表达式转换为二叉树，然后通过先序遍历二叉树的方式求出表达式的值。

一、二叉树如何表示四则运算

1.1 表达式转换为二叉树

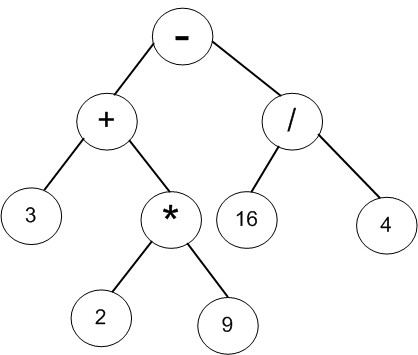
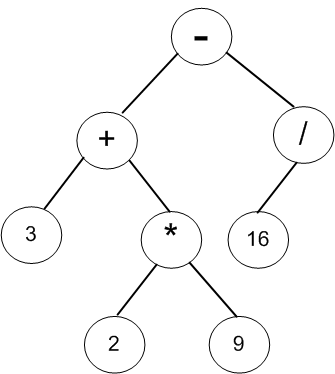
　　上图是表达式“3+2*9-16/4”转换成的二叉树，观察表达式，可以看出：

　　（1）操作数都是叶子节点；

　　（2）运算符都是内部节点；

　　（3）优先运算的操作符都在树下方，而相对优先级较低的减法（根节点）运算则最后运算。

　　从上往下看，这棵二叉树可以理解如下：

　　（1）要理解根节点"-"号的结果必须先计算出左子树"+"和右子树"/"号的结果。可以看，要想得到"+"号的结果，又必须先计算其右子树"*"号的结果；

　　（2）"*"号左右孩子是数字，可以直接计算，2*9=18。接下来计算"+"号，3+18=21，即根节点的左子树结果为21；

　　（3）"/"号左右孩子是数字，可以直接计算，16/4=4。于是，根节点的右子树结果为4。

　　（4）最后计算根节点的"-"号，21-4=17，于是得出了该表达式的值为17。

1.2 二叉表达式树的构造过程解析

　　从上面的解析过程可以看出，这是一个递归的过程，正好可以用二叉树先序遍历的方法进行计算。下面我们来一步一步地通过图示来演示一下表达式"3+2*9-16/4"解析生成二叉树的过程。

　　（1）首先获取表达式的第一个字符“3”，由于表达式树目前还是一棵空树，所以3成为根节点；

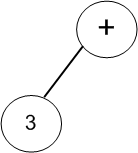
　　（2）获取第二个字符“+”，此时表达式树根节点为数字，需要将新节点作为根节点，原根节点作为新根节点的左孩子。这里需要注意的是：只有第二个节点会出现这样的可能，因为之后的根节点必定为操作符；

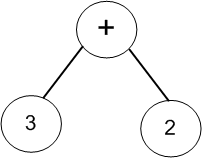
　　（3）获取第三个字符“2”，数字将沿着根节点右链插入到最右端；

　　（4）获取第四个字符“*”，如果判断到是操作符，则将与根节点比较优先级，如果新节点的优先级高则插入成为根节点的右孩子，而原根节点的右孩子则成为新节点的左子树；

　　（5）获取第五个字符“9”，数字将沿着根节点右链插入到最右端；

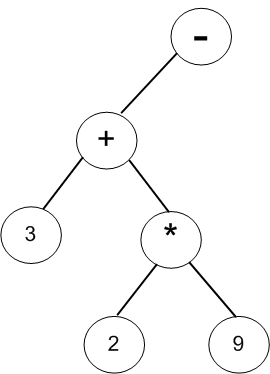
　　（6）获取第六个字符“-”，“-”与根节点“+”比较运算符的优先级，优先级相等则新节点成为根节点，原表达式树则成为新节点的左子树；

　　（7）获取第7与第8个字符组合为数字16，沿着根节点右链插入到最右端；

　　（8）获取第九个字符“/”，与根节点比较运算符的优先级，优先级高则成为根节点的右孩子，原根节点右子树则成为新节点的左子树；

　　（9）获取第十个字符“4”，还是沿着根节点右链查到最右端。至此，运算表达式已全部遍历，一棵表达式树就已经建立完成。

SUMMARY：从以上过程中我们可以将表达式树的建立算法归结如下

①第一个节点先成为表达式树的根；

②第二个节点插入时变为根节点，原根节点变为新节点的左孩子；

③插入节点为数字时，沿着根节点右链插入到最右端；

④插入节点为操作符时，先跟根节点操作符进行对比，分两种情况进行处理：

　　一是当优先级不高时，新节点成为根节点，原表达式树成为新节点的左子树；【如上面的步骤（6）】

　　二是当优先级较高时，新节点成为根节点右孩子，原根节点右子树成为新节点的左子树。【如上面的步骤（8）】

二、二叉表达式树的模拟实现

2.1 二叉表达式树节点的定义

        private class Node
        {
            private bool _isOptr;

            public bool IsOptr
            {
                get { return _isOptr; }
                set { _isOptr = value; }
            }
            private int _data;

            public int Data
            {
                get { return _data; }
                set { _data = value; }
            }
            private Node _left;

            public Node Left
            {
                get { return _left; }
                set { _left = value; }
            }
            private Node _right;

            public Node Right
            {
                get { return _right; }
                set { _right = value; }
            }

            public Node(int data)
            {
                this._data = data;
                this._isOptr = false;
            }

            public Node(char optr)
            {
                this._isOptr = true;
                this._data = optr;
            }

            public override string ToString()
            {
                if (this._isOptr)
                {
                    return Convert.ToString((char)this._data);
                }
                else
                {
                    return this._data.ToString();
                }
            }
        }

View Code

　　与普通二叉树节点定义不同，这里新增了一个isOptr标志，来判断该节点是数字节点还是运算符节点；

2.2 二叉表达式树的创建实现

        private Node CreateTree()
        {
            Node head = null;
            
            while(_pos < _expression.Length)
            {
                Node node = GetNode(); // 将当前解析字符转换为节点
                if(head == null)
                {
                    head = node;
                }
                else if (head.IsOptr == false) // 根节点为数字，当前节点为根，原根节点变为左孩子
                {
                    node.Left = head;
                    head = node;
                }
                else if (node.IsOptr == false) // 如果当前节点是数字
                {
                    // 当前节点沿右路插入最右边成为右孩子
                    Node tempNode = head;
                    while(tempNode.Right != null)
                    {
                        tempNode = tempNode.Right;
                    }
                    tempNode.Right = node;
                }
                else // 如果当前节点是运算符
                {
                    if (GetPriority((char)node.Data) <= GetPriority((char)head.Data)) // 优先级低则成为根，原二叉树成为插入节点的左子树
                    {
                        node.Left = head;
                        head = node;
                    }
                    else // 优先级高则成为根节点的右子树，原右子树成为插入节点的左子树
                    {
                        node.Left = head.Right;
                        head.Right = node;
                    }
                }
            }

            return head;
        }

　　这里按照我们在上面所归纳的创建过程算法进行了实现，代码中的注释已经比较完善，这里就不再赘述。

2.3 二叉表达式的先序遍历计算运算结果实现

        // 先序遍历进行表达式求值
        private int PreOrderCalc(Node node)
        {
            int num1, num2;
            if (node.IsOptr)
            {
                // 递归先序遍历计算num1
                num1 = PreOrderCalc(node.Left);
                // 递归先序遍历计算num2
                num2 = PreOrderCalc(node.Right);
                char optr = (char)node.Data;

                switch (optr)
                {
                    case '+':
                        node.Data = num1 + num2;
                        break;
                    case '-':
                        node.Data = num1 - num2;
                        break;
                    case '*':
                        node.Data = num1 * num2;
                        break;
                    case '/':
                        if (num2 == 0)
                        {
                            throw new DivideByZeroException("除数不能为0！");
                        }
                        node.Data = num1 / num2;
                        break;
                }
            }

            return node.Data;
        }