数据结构基础温故-4.树与二叉树（中）
在上一篇中，我们了解了树的基本概念以及二叉树的基本特点和代码实现，还用递归的方式对二叉树的三种遍历算法进行了代码实现。但是，由于递归需要系统堆栈，所以空间消耗要比非递归代码要大很多。而且，如果递归深度太大，可能系统撑不住。因此，我们使用非递归（这里主要是循环，循环方法比递归方法快, 因为循环避免了一系列函数调用和返回中所涉及到的参数传递和返回值的额外开销）来重新实现一遍各种遍历算法，再对二叉树的另外一种特殊的遍历—层次遍历进行实现，最后再了解一下特殊的二叉树—二叉查找树。
在上一篇中，我们了解了树的基本概念以及二叉树的基本特点和代码实现，还用递归的方式对二叉树的三种遍历算法进行了代码实现。但是，由于递归需要系统堆栈，所以空间消耗要比非递归代码要大很多。而且，如果递归深度太大，可能系统撑不住。因此，我们使用非递归（这里主要是循环，循环方法比递归方法快, 因为循环避免了一系列函数调用和返回中所涉及到的参数传递和返回值的额外开销）来重新实现一遍各种遍历算法，再对二叉树的另外一种特殊的遍历—层次遍历进行实现，最后再了解一下特殊的二叉树—二叉查找树。
一、递归与循环的区别及比较
1.1 递归为何很慢？
大家都知道递归的实现是通过调用函数本身，函数调用的时候，每次调用时要做地址保存，参数传递等，这是通过一个递归工作栈实现的。具体是每次调用函数本身要保存的内容包括：局部变量、形参、调用函数地址、返回值。那么，如果递归调用 N 次，就要分配 N*局部变量、N*形参、N*调用函数地址、N*返回值，这势必是影响效率的。
关于系统栈和用户栈：
①系统栈（也叫核心栈、内核栈）是内存中属于操作系统空间的一块区域，其主要用途为： (1)保存中断现场，对于嵌套中断，被中断程序的现场信息依次压入系统栈，中断返回时逆序弹出； (2)保存操作系统子程序间相互调用的参数、返回值、返回点以及子程序(函数)的局部变量。
②用户栈是用户进程空间中的一块区域，用于保存用户进程的子程序间相互调用的参数、返回值、返回点以及子程序(函数)的局部变量。
我们编写的递归程序属于用户程序，因此使用的是用户栈。
1.2 循环会快些吗？
递归与循环是两种不同的解决问题的典型思路。当然也并不是说循环效率就一定比递归高，递归和循环是两码事，递归带有栈操作，循环则不一定，两个概念不是一个层次，不同场景做不同的尝试。
（1）递归算法：
①优点：代码简洁、清晰，并且容易验证正确性。
②缺点：它的运行需要较多次数的函数调用，如果调用层数比较深，需要增加额外的堆栈处理（还有可能出现堆栈溢出的情况），比如参数传递需要压栈等操作，会对执行效率有一定影响。但是，对于某些问题，如果不使用递归，那将是极端难看的代码。
（2）循环算法：
①优点：速度快，结构简单。
②缺点：并不能解决所有的问题。有的问题适合使用递归而不是循环。但是如果使用循环并不困难的话，最好使用循环。
（3）递归与循环的对比总结：
①一般递归调用可以处理的算法，也通过循环去解决常需要额外的低效处理。
②现在的编译器在经过优化后，对于多次调用的函数处理会有非常好的效率优化，效率未必低于循环。
③递归和循环两者完全可以互换。如果用到递归的地方可以很方便使用循环替换，而不影响程序的阅读，那么替换成递归往往是好的。（例如：求阶乘的递归实现与循环实现。）
二、二叉树的非递归遍历实现
2.1 前序遍历的非递归实现
// Method01:前序遍历 public void PreOrderNoRecurise(Node<T> node) { if (node == null) { return; } // 根->左->右 Stack<Node<T>> stack = new Stack<Node<T>>(); stack.Push(node); Node<T> tempNode = null; while (stack.Count > 0) { // 1.遍历根节点 tempNode = stack.Pop(); Console.Write(tempNode.data); // 2.右子树压栈 if (tempNode.rchild != null) { stack.Push(tempNode.rchild); } // 3.左子树压栈(目的：保证下一个出栈的是左子树的节点) if (tempNode.lchild != null) { stack.Push(tempNode.lchild); } } }
在该方法中，利用了栈的先进后出的特性，首先遍历显示根节点，然后将右子树（注意是右子树不是左子树）压栈，最后将左子树压栈。由于最后时将左子树节点压栈，所以下一次首先出栈的应该是左子树的根节点，也就保证了先序遍历的规则。
2.2 中序遍历的非递归实现
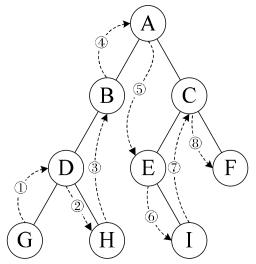
public void MidOrderNoRecurise(Node<T> node) { if (node == null) { return; } // 左->根->右 Stack<Node<T>> stack = new Stack<Node<T>>(); Node<T> tempNode = node; while (tempNode != null || stack.Count > 0) { // 1.依次将所有左子树节点压栈 while(tempNode != null) { stack.Push(tempNode); tempNode = tempNode.lchild; } // 2.出栈遍历节点 tempNode = stack.Pop(); Console.Write(tempNode.data); // 3.左子树遍历结束则跳转到右子树 tempNode = tempNode.rchild; } }
在该方法中，首先将根节点所有的左子树节点压栈，然后一一出栈，每当出栈一个元素后，便将其右子树节点压栈。这样就可以实现首先出栈的永远是栈中的左子树节点，然后是根节点，最后时右子树节点，也就可以保证中序遍历的规则。
2.3 后序遍历的非递归实现
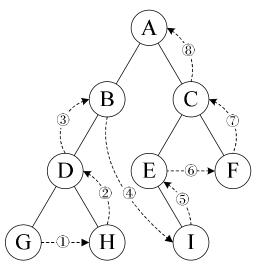
public void PostOrderNoRecurise(Node<T> node) { if (root == null) { return; } // 两个栈：一个存储，一个输出 Stack<Node<T>> stackIn = new Stack<Node<T>>(); Stack<Node<T>> stackOut = new Stack<Node<T>>(); Node<T> currentNode = null; // 根节点首先压栈 stackIn.Push(node); // 左->右->根 while (stackIn.Count > 0) { currentNode = stackIn.Pop(); stackOut.Push(currentNode); // 左子树压栈 if (currentNode.lchild != null) { stackIn.Push(currentNode.lchild); } // 右子树压栈 if (currentNode.rchild != null) { stackIn.Push(currentNode.rchild); } } while (stackOut.Count > 0) { // 依次遍历各节点 Node<T> outNode = stackOut.Pop(); Console.Write(outNode.data); } }
在该方法中，使用了两个栈来辅助，其中一个stackIn作为中间存储起到过渡作用，而另一个stackOut则作为最后的输出结果进行遍历显示。众所周知，栈的特性使LIFO（后进先出），那么stackIn在进行存储过渡时，先按照根节点->左孩子->右孩子的顺序依次压栈，那么其出栈顺序就是右孩子->左孩子->根节点。而每当循环一次就会从stackIn中出栈一个元素，并压入stackOut中，那么这时stackOut中的出栈顺序则变成了左孩子->右孩子->根节点的顺序，也就符合了后序遍历的规则。
2.4 层次遍历的实现
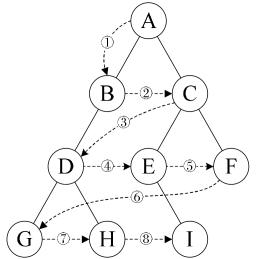
public void LevelOrder(Node<T> node) { if (root == null) { return; } Queue<Node<T>> queueNodes = new Queue<Node<T>>(); queueNodes.Enqueue(node); Node<T> tempNode = null; // 利用队列先进先出的特性存储节点并输出 while (queueNodes.Count > 0) { tempNode = queueNodes.Dequeue(); Console.Write(tempNode.data); if (tempNode.lchild != null) { queueNodes.Enqueue(tempNode.lchild); } if (tempNode.rchild != null) { queueNodes.Enqueue(tempNode.rchild); } } }
在该方法中，使用了一个队列来辅助实现，队列是遵循FIFO（先进先出）的，与栈刚好相反，所以，我们这里只需要按照根节点->左孩子->右孩子的入队顺序依次入队，输出时就可以符合根节点->左孩子->右孩子的规则了。
2.5 各种非递归遍历的测试
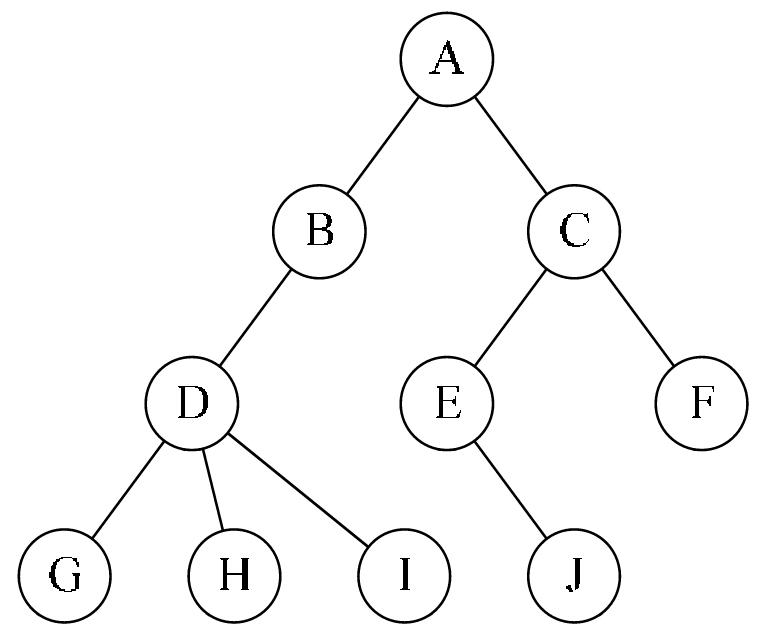
上面我们实现了非递归方式的遍历算法，这里我们对其进行一个简单的测试。跟上一篇相同首先创建一棵如下图所示的二叉树，然后调用非递归版的先序、中序、后序以及层次遍历方法查看遍历结果。
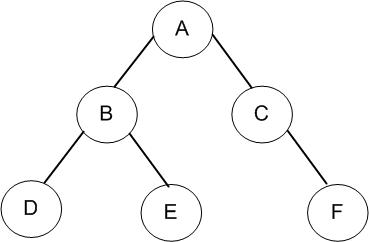
（1）测试代码：
static void MyBinaryTreeBasicTest() { // 构造一颗二叉树，根节点为"A" MyBinaryTree<string> bTree = new MyBinaryTree<string>("A"); Node<string> rootNode = bTree.Root; // 向根节点"A"插入左孩子节点"B"和右孩子节点"C" bTree.InsertLeft(rootNode, "B"); bTree.InsertRight(rootNode, "C"); // 向节点"B"插入左孩子节点"D"和右孩子节点"E" Node<string> nodeB = rootNode.lchild; bTree.InsertLeft(nodeB, "D"); bTree.InsertRight(nodeB, "E"); // 向节点"C"插入右孩子节点"F" Node<string> nodeC = rootNode.rchild; bTree.InsertRight(nodeC, "F"); // 计算二叉树目前的深度 Console.WriteLine("The depth of the tree : {0}", bTree.GetDepth(bTree.Root)); // 前序遍历 Console.WriteLine("---------PreOrder---------"); bTree.PreOrder(bTree.Root); // 中序遍历 Console.WriteLine(); Console.WriteLine("---------MidOrder---------"); bTree.MidOrder(bTree.Root); // 后序遍历 Console.WriteLine(); Console.WriteLine("---------PostOrder---------"); bTree.PostOrder(bTree.Root); Console.WriteLine(); // 前序遍历（非递归） Console.WriteLine("---------PreOrderNoRecurise---------"); bTree.PreOrderNoRecurise(bTree.Root); // 中序遍历（非递归） Console.WriteLine(); Console.WriteLine("---------MidOrderNoRecurise---------"); bTree.MidOrderNoRecurise(bTree.Root); // 后序遍历（非递归） Console.WriteLine(); Console.WriteLine("---------PostOrderNoRecurise---------"); bTree.PostOrderNoRecurise(bTree.Root); Console.WriteLine(); // 层次遍历 Console.WriteLine("---------LevelOrderNoRecurise---------"); bTree.LevelOrder(bTree.Root); }
（2）运行结果：
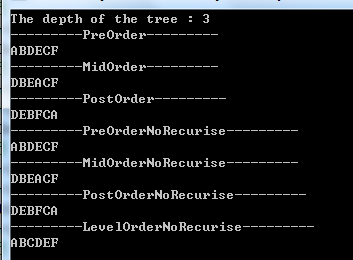
三、二叉查找树又是什么鬼？
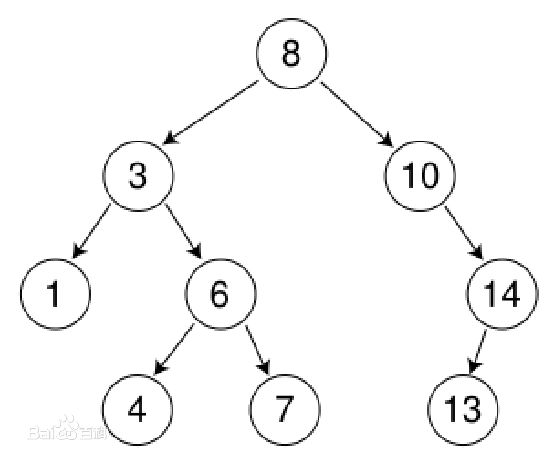
二叉查找树（Binary Search Tree）又称二叉排序树（Binary Sort Tree），亦称二叉搜索树。它具有以下几个性质：
（1）若左子树不空，则左子树上所有结点的值均小于它的根结点的值；
（2）若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值；
（3）左、右子树也分别为二叉排序树；
（4）没有键值相等的节点。
对于二叉查找树，我们只需要进行一次中序遍历便可以得到一个排序后的遍历结果。
四、二叉查找树的实现
4.1 新节点的插入
二叉查找树的插入过程大致为以下几个步骤：
Step1.若当前的二叉查找树为空，则插入的元素为根节点；
--> Step2.若插入的元素值小于根节点值，则将元素插入到左子树中；
--> Step3.若插入的元素值不小于根节点值，则将元素插入到右子树中。
public void InsertNode(int data) { Node newNode = new Node(); newNode.data = data; if (this.root == null) { this.root = newNode; } else { Node currentNode = this.root; Node parentNode = null; while(currentNode != null) { parentNode = currentNode; if(currentNode.data < data) { currentNode = currentNode.rchild; } else { currentNode = currentNode.lchild; } } if(parentNode.data < data) { // 若插入的元素值小于根节点值，则将元素插入到左子树中 parentNode.rchild = newNode; } else { // 若插入的元素值不小于根节点值，则将元素插入到右子树中 parentNode.lchild = newNode; } } }
对如上图所示的二叉查找树进行构造：
MyBinarySearchTree bst = new MyBinarySearchTree(8); bst.InsertNode(3); bst.InsertNode(10); bst.InsertNode(1); bst.InsertNode(6); bst.InsertNode(14); bst.InsertNode(4); bst.InsertNode(7); bst.InsertNode(13); Console.WriteLine("----------LevelOrder----------"); bst.LevelOrder(bst.Root);
层次遍历的显示结果如下图所示：
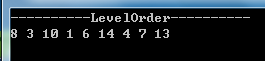
4.2 老节点的移除
二叉查找树的删除过程相比插入过程要复杂一些，这里主要分三种情况进行处理：
Scene1.节点p为叶子节点：直接删除该节点，再修改其父节点的指针（注意分是根节点和不是根节点），如图(a)；
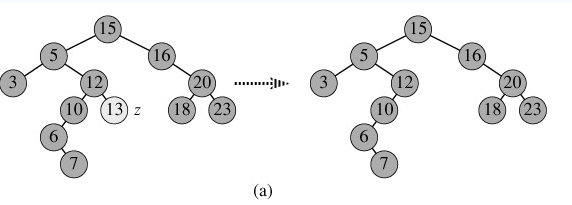
Scene2.节点p为单支节点（即只有左子树或右子树）：让p的子树与p的父亲节点相连，再删除p即可；（注意分是根节点和不是根节点两种情况），如图b；
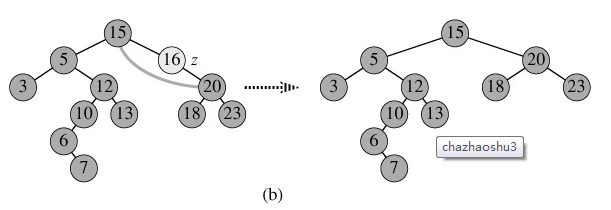
Scene3.节点p的左子树和右子树均不为空：首先找到p的后继y，因为y一定没有左子树，所以可以删除y，并让y的父亲节点成为y的右子树的父亲节点，并用y的值代替p的值；或者可以先找到p的前驱x，x一定没有右子树，所以可以删除x，并让x的父亲节点成为y的左子树的父亲节点。如图c。
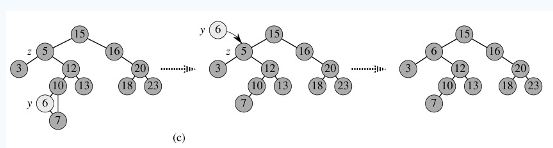
通过代码实现如下：
public void RemoveNode(int key) { Node current = null, parent = null; // 定位节点位置 current = FindNode(key); // 没找到data为key的节点 if (current == null) { Console.WriteLine("没有找到data为{0}的节点!", key); return; } #region 1.如果该节点是叶子节点 if (current.lchild == null && current.rchild == null) // 如果该节点是叶子节点 { if (current == this.root) // 如果该节点为根节点 { this.root = null; } else if (parent.lchild == current) // 如果该节点为左孩子节点 { parent.lchild = null; } else if (parent.rchild == current) // 如果该节点为右孩子节点 { parent.rchild = null; } } #endregion #region 2.如果该节点是单支节点 else if (current.lchild == null || current.rchild == null) // 如果该节点是单支节点 (只有一个左孩子节点或者一个右孩子节点) { if (current == this.root) // 如果该节点为根节点 { if (current.lchild == null) { this.root = current.rchild; } else { this.root = current.lchild; } } else { if (parent.lchild == current && current.lchild != null) // p是q的左孩子且p有左孩子 { parent.lchild = current.lchild; } else if (parent.lchild == current && current.rchild != null) // p是q的左孩子且p有右孩子 { parent.rchild = current.rchild; } else if (parent.rchild == current && current.lchild != null) // p是q的右孩子且p有左孩子 { parent.rchild = current.lchild; } else // p是q的右孩子且p有右孩子 { parent.rchild = current.rchild; } } } #endregion #region 3.如果该节点的左右子树均不为空 else // 如果该节点的左右子树均不为空 { Node t = current; Node s = current.lchild; // 从p的左子节点开始 // 找到p的前驱，即p左子树中值最大的节点 while(s.rchild != null) { t = s; s = s.rchild; } current.data = s.data; // 把节点s的值赋给p if (t == current) { current.lchild = s.lchild; } else { current.rchild = s.rchild; } } #endregion } // 根据Key查找某个节点 public Node FindNode(int key) { Node currentNode = this.root; while (currentNode != null && currentNode.data != key) { if (currentNode.data < key) { currentNode = currentNode.rchild; } else if (currentNode.data > key) { currentNode = currentNode.lchild; } else { break; } } return currentNode; }
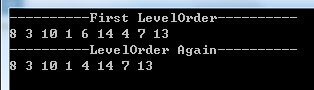
在上面的示例中移除既有左孩子又有右孩子的节点6后的层次遍历结果如下图所示：
附件下载
本文所实现的C#版二叉树的代码：http://pan.baidu.com/s/1gdjKwKF
参考资料
（1）程杰，《大话数据结构》
（2）陈广，《数据结构（C#语言描述）》
（3）段恩泽，《数据结构（C#语言版）》
（4）VincentCZW，《递归的效率问题以及与循环的比较》
（5）HelloWord，《循环与递归的区别》
（6）爱也玲珑，《二叉查找树—插入、删除与查找》
