线性代数笔记5——平面方程与矩阵
线性方程的几何意义
二元线性方程
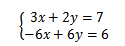
该方程是一个二元线性方程组,包含两个方程,每个方程是一条直线,两条直线的交点就是该方程有唯一解,这就是二元线性方程的几何意义。
平面方程
空间内不在同一直线上的三点构成一个平面,平面方程可表示为ax + by + cz = d。平面方程也称为三元线性方程。
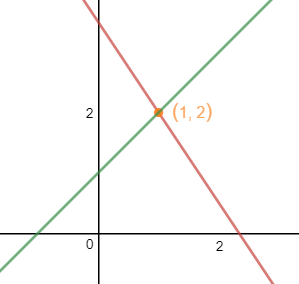
方程x + 4y + z = 8,在xyz三个坐标轴上的截距分别是(8,0,0),(0,2,0),(0,0,8),下图是该函数在坐标轴上的示意图:
需要注意的是,平面是无限延伸的。
根据法向量求平面方程
现在需要找到一个过原点的平面,它有一个过原点的法向量是<1, 5, 10>。
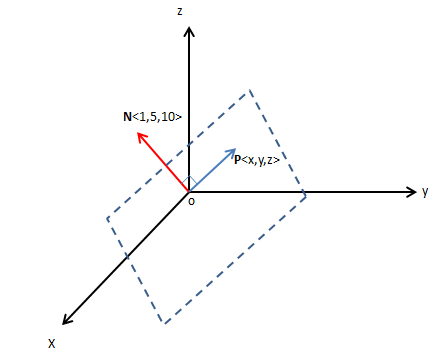
如上图所示,P<x, y, z>是所求平面上的向量,法向量N⊥OP,因此:
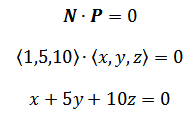
这就是平面方程。
再看一个稍微不同点的问题,一个平面的法向量是N<1, 5, 10>,该平面经过P0(2, 1, -1),求该平面方程。
由于拥有同一个法向量,所以这是与上一个平面平行的平面:
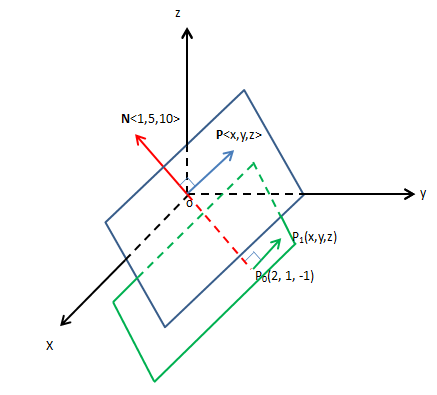
平面上的任意点P1是(x, y, z),向量P0P1⊥N:
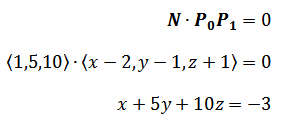
上面两个方程唯一的不同点就是ax + by + cz = d 中的d,其它参数对应了穿过原点的法向量,实际上,d两个平行平面的距离。根据这个特点,可以很快求得第二个平面方程:
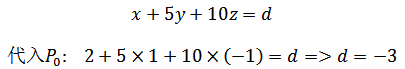
示例
向量V = <1, 2, -1>与平面x + y + 3z = 5的关系?
平面的法向量N = <1, 1, 3>,容易看出,V·N = 1×1 + 2×1 + (-1)×3 = 0,V⊥N,向量V与平面平行。需要注意的是,向量不是点(实际上向量有无数点),<1, 2, -1>不同于(1, 2, -1),在没有特殊说明的情况下,可以认为向量从原点出发。如果向量V从原点出发,V经过点(1, 2, -1),但该点并不在平面上。
平面方程组的解
三元线性方程组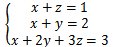 ,设三个平面分别是P1,P2,P3,该方程组有唯一解,即这三个平面相交于一点,三个方程两两相交于一条直线:
,设三个平面分别是P1,P2,P3,该方程组有唯一解,即这三个平面相交于一点,三个方程两两相交于一条直线:
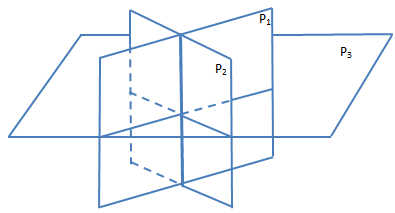
平面方程组也可能出现无解的情况,一种典型的情况是三个平面平行。如果P1∩P2≠φ,即二者相交于一条直线,根据P3的位置,平面方程组可能有唯一解,无解,或有无数解。下面是无数解和无解的情况:
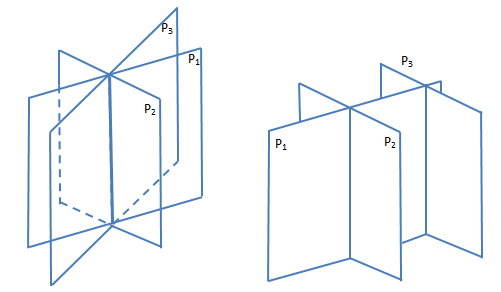
无数解和无解
总结一下,如果P1与P2相交,它们的交线:
- 与P3相交于一点,则方程组有唯一解;
- 在P3上,则方程组有无数解;
- 与P3平行,且不在P3上,方程组无解。
当然,如果P3与P1或P2中一个相同,则结集是一个平面。
点到平面的距离
平面方程是ax + by + cz = d,平面外一点P = (x0, y0, z0),求该点到平面的距离。
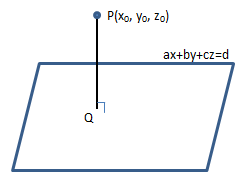
PQ垂直于平面,现在要求PQ的长度,但是并不知道Q点的具体数值。
设P’ = (x1, y1, z1)是平面上的一点,现在将问题转换为向量:
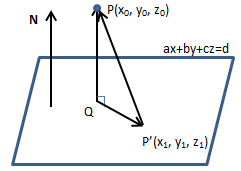
向量QP是P’ P在法向量N方向上的分量,也就是P’ P与N相同方向的单位向量的点积。(可参考《线性代数笔记3——向量2(点积)》)设距离为D,则:
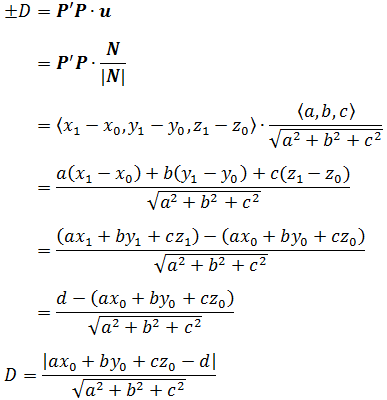
求解线性方程
当然可以使用初中的代数知识求解线性方程组,这里主要讨论如何用矩阵求解。
消元法

首先将方程组以矩阵的方式表示:
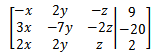
该矩阵称为增广矩阵。由于是线性方程组,可以省略未知数:
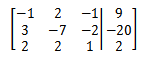
现在可以对其进行消元,首先消去x,方法与普通代数法类似:
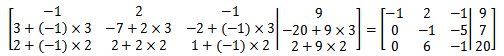
用同样的方法对y消元:
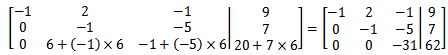
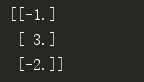
矩阵第三行对应-31z = 62,z = -2
最终可解得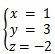
可以看出,消元法本质上与初中的代数法没有区别,只是换了一种较为简单的表现形式,对于多元线性方程组,其消元过程十分繁琐。
矩阵法
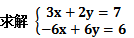
这里需要使用列向量的概念,列向量是一个 n×1 的矩阵,即矩阵由一个含有n个元素的列所组成:列向量的转置是一个行向量,反之亦然。
将上面的方程组用矩阵和向量表示:
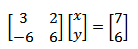
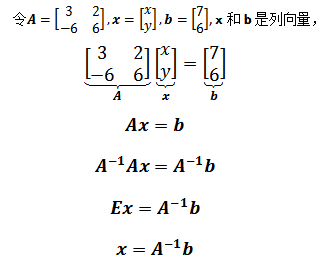
实际上可看作 x = b/A,有点意思了,可以通过一个除法运算直接求得方程的解。
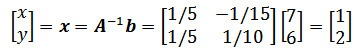
解得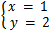
对于多元线性方程组,使用矩阵法求解比消元法简单的多。
我们用python求解消元法中的方程组
1 import numpy as np
2
3 a = np.matrix([[-1,2,-1],[3,-7,-2],[2,2,1]])
4 c = np.matrix([[9,-20,2]]).T
5 result = a**-1 * c
6 print(result)
无解的方程组
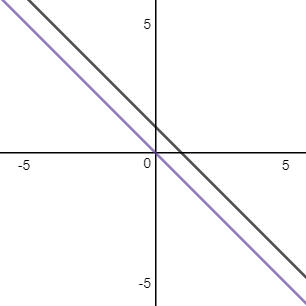
线性方程组在用矩阵向量法转换后,如果矩阵A是奇异矩阵,A-1没有定义,该方程组无解。对于二元线性方程组来说,其几何意义是两条平行的直线。
如 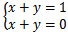 ,该方程组无解,
,该方程组无解, 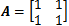 是奇异矩阵。下图是该方程组在坐标轴上的图像:
是奇异矩阵。下图是该方程组在坐标轴上的图像:
多个线性方程组
现在来看下面的矩阵:
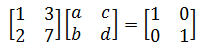
如果把这个矩阵根据乘法展开,将得到两个矩阵:
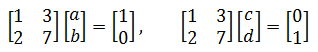
这就可以看作是两个线性方程组:AX1 = b1,AX2 = b2
消元法求逆矩阵
上面的示例中, 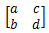 是
是 的逆,现在尝试用消元法求解。增广矩阵形式:
的逆,现在尝试用消元法求解。增广矩阵形式:
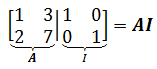
我们的目标是将其变为IA-1:
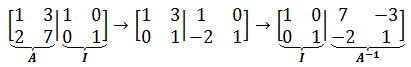
示例
示例1
求下面的平面方程:
a) 已知平面的法向量N = <1, 2, 3>,平面过点(1, 0, -1)
b) 平面过原点且平行于两个向量A = <1, 0, -1>和B = <-1, 2, 0>
c) 平面过点P1(1, 2, 0), P2(3, 1, 1), P3(2, 0, 0)
d) 平面与a中的平面平行,且经过点(1 , 2, 3)
a.
平面方程ax + by + cz = d,N = <1, 2, 3> =<a, b, c>,所以平面方程是x + 2y + 3z = d
将点(1, 0, -1) 代入平面方程,1 + 0 -3 = -2 = d
平面方程是 x + 2y + 3z = -2
b.
平面方程ax + by + cz = d
∵A,B过原点,且与平面平行,并且平面过原点
∴A,B在平面上,d = 0
已知平面上两个个向量从同一点出发的向量,计算平面的法向量:
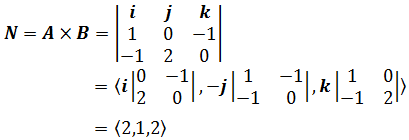
平面方程是 2x + y + 2z = 0
根据叉积计算法向量可参考《线性代数笔记4——向量3(叉积)》
c.
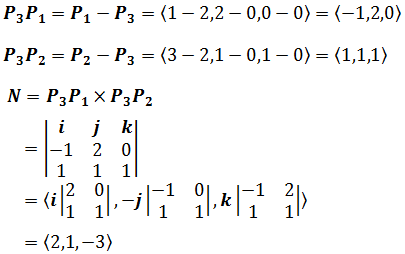
平面方程2x + y – 3z = d,取任意点代入,d = 4。平面方程是2x + y – 3z = 4
d.
a的平面是x + 2y + 3z = -2,由于该平面平行于a,所以该平面是x + 2y + 3z = d。
将点(1 , 2, 3)代入,1 + 2×2 + 3×3 = 14 = d
平面方程是x + 2y + 3z = 14
示例2
求原点到平面2x + y -2z = 4的距离。
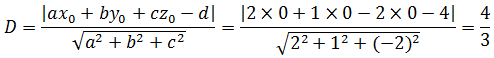
总结
- 二元线性方程组的几何意义是平面上的两条直线,其解是二者的交点
- 三元线性方程组的几何意义是三维空间上的三个平面,可能存在唯一解、无数解或无解
- 平面方程用ax + by + cz = d,点到平面的距离
![]()
- 如果线性方程组对应的矩阵是奇异矩阵,则该方程组无解
作者:我是8位的
出处:http://www.cnblogs.com/bigmonkey
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!

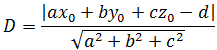


 浙公网安备 33010602011771号
浙公网安备 33010602011771号