【bzoj2121】字符串游戏 区间dp

题目描述

给你一个字符串L和一个字符串集合S，如果S的某个子串在S集合中，那么可以将其删去，剩余的部分拼到一起成为新的L串。问：最后剩下的串长度的最小值。

输入

输入的第一行包含一个字符串，表示L。

第二行包含一个数字n，表示集合S中元素个数。

以下n行，每行一个字符串，表示S中的一个元素。

输入字符串都只包含小写字母。

输出

输出一个整数，表示L的最短长度。

样例输入

aaabccd
3
ac
abc
aaa

样例输出

2

---

题解

我们考虑：每次删除连续的一段，对应到原串上即：删除 $[l,r]$ 中所有未被删除的字符。其中 $l,r$ 都未被删除。

这样就相当于选择若干区间来删除。

注意到选择的任意两个区间要么包含要么不相交（相离），对于相邻的相离的也可以看作是包含（右区间左端点看作是左区间左端点，即一个空位置），因此只有包含关系。

那么如下图：

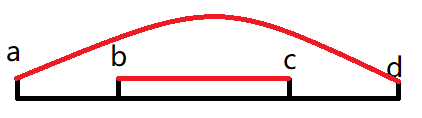
先选择 $[b,c]$ 的串 $S$ ，再选择 $[a,d]$ 的串 $T$ ，可以看作是处理出 $[a,b)$ 能够匹配到 $T$ 的中间位置，$[b,c]$ 能够匹配到 $S$ 的结束位置（即删除掉），进而推知 $[a,c]$ 能够匹配到 $T$ 的中间位置，再向右匹配得知 $[a,d]$ 能够匹配到 $T$ 的结束位置。

考虑区间dp。设 $f[l][r]$ 表示 $[l,r]$ 是否可以全部删掉，再设 $g[l][r][i][j]$ 表示 $[l,r]$ 是否能够删成第 $i$ 个字符串的前 $j$ 个字符。

那么考虑区间 $[l,r]$ ，如果进行匹配的话转移为 $g[l][r][i][j]=g[l][r-1][i][j-1]$ ，前提条件 $str[r]==w[i][j]$ ，即区间右端点和第 $i$ 个串的第 $j$ 个字符相同。

如果不进行匹配的话，$r$ 一定在某个 $[k,r]$ 中被消掉，因此枚举 $k\in[l,r]$ ，转移为 $g[l][r][i][j]=g[l][k-1][i][j]\&\&f[k][r]$ 。

根据 $f$ 的定义有转移 $f[l][r]=g[l][r][i][len[i]]$ 。

这样我们就能够推出 $f$ 和 $g$ 。

再考虑答案：设 $h[i]$ 表示前 $i$ 个字符的答案，那么 $h[i]=h[i-1]+1$ ；如果某个 $j$ 满足 $f[j][i]=1$ ，即 $[j,i]$ 能删掉，则还有 $h[i]=h[j-1]$ 。

最终答案就是 $h[n]$ 。

时间复杂度 $O(n^3·m·len)$ 

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
bool f[155][155] , g[155][155][35][25];
char str[155] , w[35][25];
int c[35] , ans[155];
int main()
{
	int n , m , len , l , r , i , j , k;
	scanf("%s%d" , str + 1 , &m) , n = strlen(str + 1);
	for(i = 1 ; i <= m ; i ++ ) scanf("%s" , w[i] + 1) , c[i] = strlen(w[i] + 1);
	for(i = 1 ; i <= n ; i ++ )
	{
		f[i][i - 1] = 1;
		for(j = 1 ; j <= m ; j ++ )
			g[i][i - 1][j][0] = 1;
	}
	for(len = 1 ; len <= n ; len ++ )
	{
		for(l = 1 ; l <= n - len + 1 ; l ++ )
		{
			r = l + len - 1;
			for(i = 1 ; i <= m ; i ++ )
			{
				for(j = 1 ; j <= c[i] ; j ++ )
					if(str[r] == w[i][j])
						g[l][r][i][j] |= g[l][r - 1][i][j - 1];
				for(j = 0 ; j <= c[i] ; j ++ )
					for(k = l ; k <= r ; k ++ )
						g[l][r][i][j] |= g[l][k - 1][i][j] & f[k][r];
			}
			for(i = 1 ; i <= m ; i ++ ) f[l][r] |= g[l][r][i][c[i]];
		}
	}
	for(i = 1 ; i <= n ; i ++ )
	{
		ans[i] = ans[i - 1] + 1;
		for(j = 1 ; j <= i ; j ++ )
			if(f[j][i])
				ans[i] = min(ans[i] , ans[j - 1]);
	}
	printf("%d\n" , ans[n]);
	return 0;
}