线性方程组 solve a system of linear equations

求解线性方程组 solve a system of linear equations

---

​ 方程组（system of equations），一般有\(n\)个方程和\(n\)个未知数。对于线性方程组（system of linear equations），即未知数的幂都是1的方程组，通常，在中学阶段，我们会一般使用联立求解的方法求解出未知数（比如说\(x\)，或者\(y\)等），那么有没有什么其他方法也能求解出线性方程组呢？
​ 我们如果将方程组以一个新的形式表达出来，比如说：

\[\left\{\begin{matrix} 2x&-y&=&0 \\ -x&+2y&=&3 \end{matrix}\right. \]

这个方程组以矩阵（matrix）形式表示：

\[\begin{bmatrix} 2 & -1 \\ -1 & 2 \\ \end{bmatrix} \begin{bmatrix} x \\y \end{bmatrix} =\begin{bmatrix} 0 \\ 3\end{bmatrix} \]

表示成形似\(\mathbf A\symbfit x =\mathbf b\)的格式，其中\(\mathbf A\)称为系数矩阵，\(\symbfit x\)则是未知数向量。

​ 我们考虑这样一个事情，对于线性方程组，其结果无非就可以看做每个线性方程对应的几何图形的交集，比如说上述二元方程组就可以用两直线求交点得出解：

​ 绘制行图像（row picture）：

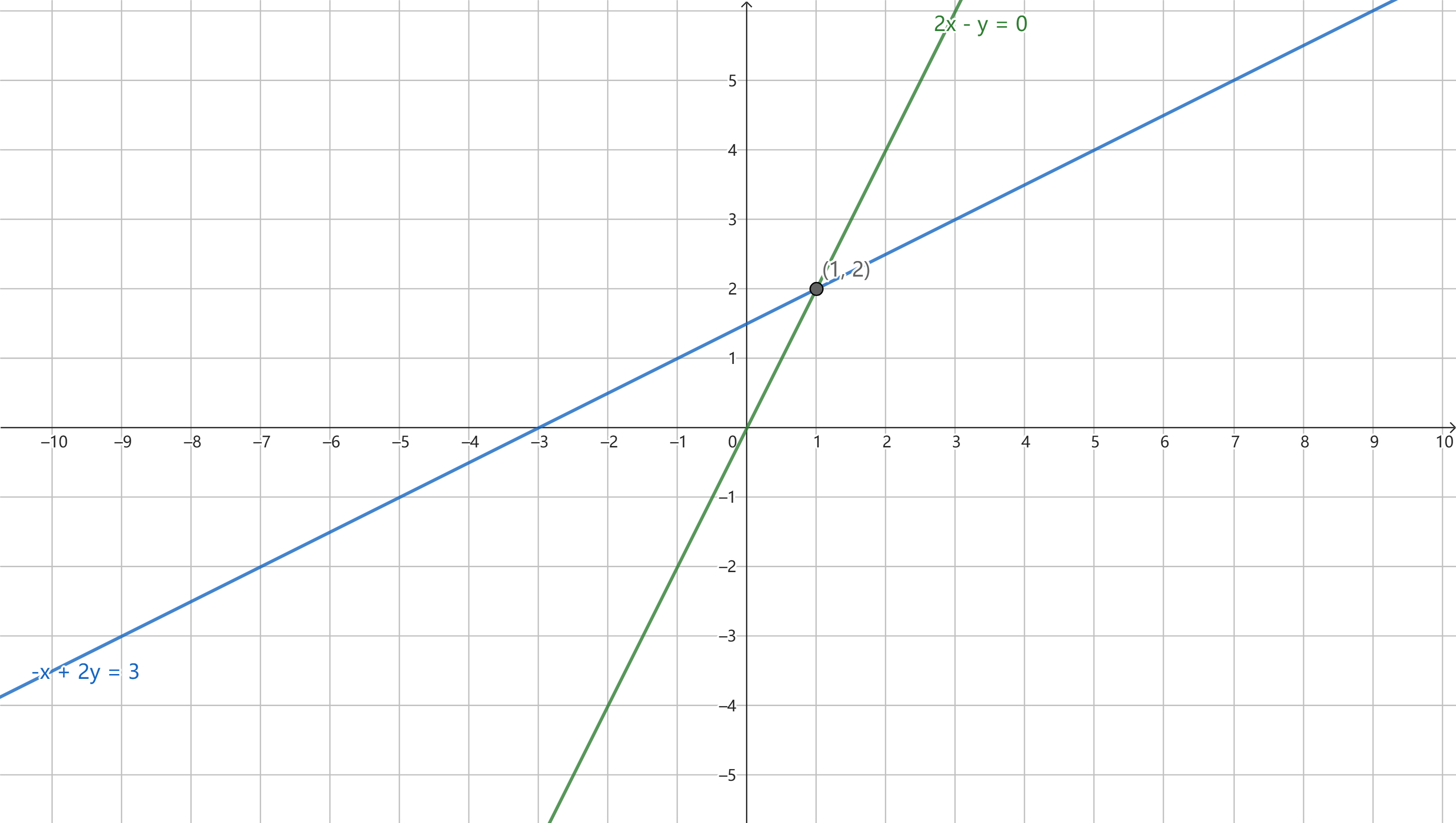
​ 得到交点为\((1,2)\)，则显然方程组的解也是如此。所谓“线性”，简单理解就是“直线”（这样说有点不严谨，但是不妨碍我们最初这么理解），这样实际上就把线性方程组和几何联系起来了。

​ 那么我们再换个思路，考虑如下写法：

\[x\begin{bmatrix} 2\\-1 \end{bmatrix} + y\begin{bmatrix} -1\\2 \end{bmatrix} = \begin{bmatrix} 0\\3 \end{bmatrix} \]

我们不妨试想一下，线性方程组的求解问题是不是可以考虑成将等式左边的两个向量正确组合，构成等式右边的向量，即对列向量的线性组合（linear combination of the columns）？既然有这个想法，那么不妨试实现一下：

​ 在之前我们已经解出来\(x\)和\(y\)的值，向上式代入：

\[1\begin{bmatrix} 2\\-1 \end{bmatrix} + 2\begin{bmatrix} -1\\2 \end{bmatrix} = \begin{bmatrix} 0\\3 \end{bmatrix} \]

这个可以看做为\(1\)倍向量\(\begin{bmatrix}2\\-1\end{bmatrix}\)和\(2\)倍向量\(\begin{bmatrix}-1\\2\end{bmatrix}\)的和向量，如下图：

​ 绘制列图像（column picture）：

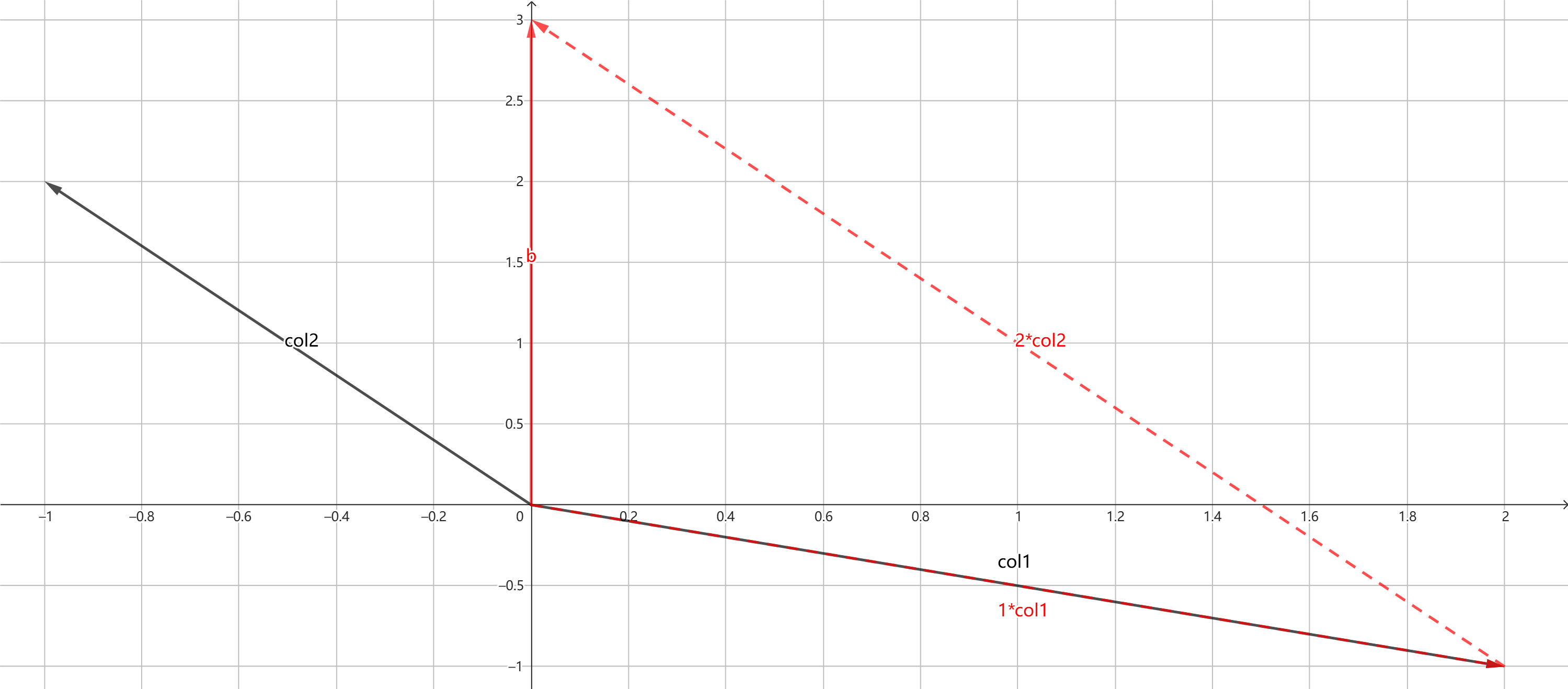
​ 因此，求解线性方程组可以看作为对系数矩阵列向量的线性组合。显然，如果我们保持左边列向量不变，改变\(x\)和\(y\)，便可以得到整个平面任意的向量（当然，前提是这两个列向量不共线）。

​ 以上是二维条件下的情况，现在我们再考虑三维条件下的情况：

​ 考虑线性方程组

\[\left\{\begin{matrix} 2x&-y&&=&0 \\ -x&+2y&-z&=&-1\\ &-3y&+4z&=&4 \end{matrix}\right. \]

得到其系数矩阵\(A=\begin{bmatrix}2&-1&0\\-1&2&-1\\0&-3&4\end{bmatrix}\)，\(b=\begin{bmatrix}0\\-1\\4\end{bmatrix}\)。

​ 绘制行图像：

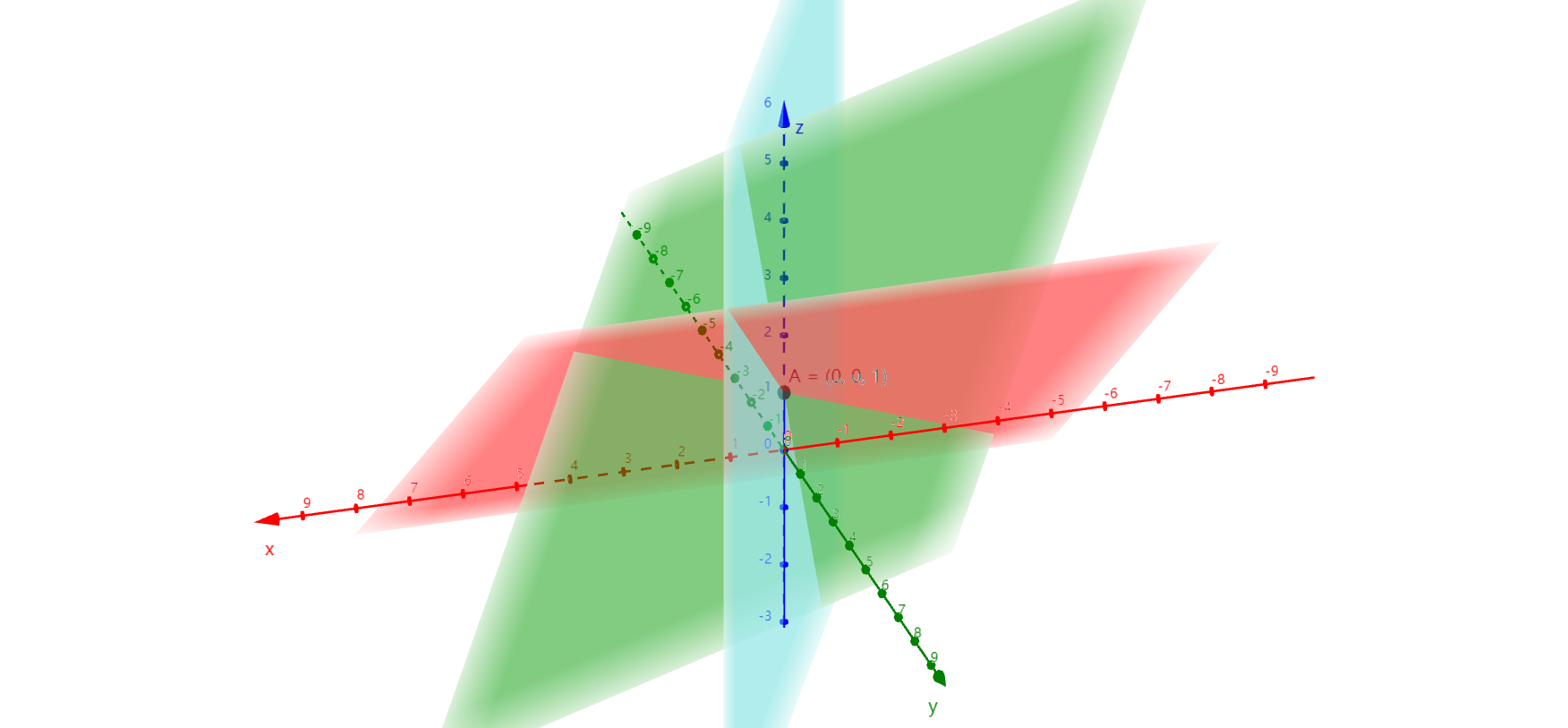
​ 三个线性方程对应的三个平面交集为一个点\((0,0,1)\)。

​ 和之前的类似，我们再看一下这个写法：

\[x\begin{bmatrix} 2\\-1\\0 \end{bmatrix} + y\begin{bmatrix} -1\\2\\-3 \end{bmatrix} + z\begin{bmatrix} 0\\-1\\4 \end{bmatrix} = \begin{bmatrix} 0\\-1\\4 \end{bmatrix} \]

由于这个线性方程组比较特殊，我们可以看到等式左边第三个列向量等于等式右边的向量。因此我们可以设置\(x=y=0,z=1\)得到

​ 经过上述两个例子，我们不禁会有一个问题，就是是否对于任意\(b\)，都能求解\(A\symbfit x = b\)？换句话说，列向量的线性组合都能覆盖整个三维区间吗？

​ 在二维的例子中，我们就说到过，如果两个向量共线，那么显然不可以组合成二维空间中任意一个向量。三维空间同理，如果三个向量共面，则也不可行。当然，这个例子中的系数矩阵是可以的，这种矩阵称为非奇异的（non-singular）或者可逆的（invertible）。

​ 最后，再说一下矩阵乘法，最一开始我们提到的\(\mathbf A\symbfit x =\mathbf b\)中的\(\mathbf b\)向量就是\(\mathbf A\)与\(\symbfit x\)的乘积。

​ 矩阵的乘法有如下两种数值计算方法。比如说：

\[\begin{bmatrix} 2 & 5\\ 1 & 3 \end{bmatrix} \begin{bmatrix} 1\\ 2 \end{bmatrix} \]

​ 第一种方法：

\[\begin{bmatrix} 2 & 5\\ 1 & 3 \end{bmatrix} \begin{bmatrix} 1\\ 2 \end{bmatrix} = 1\begin{bmatrix} 2\\ 1 \end{bmatrix} + 2\begin{bmatrix} 5\\ 3 \end{bmatrix} =\begin{bmatrix} 12\\ 7 \end{bmatrix} \]

这种解法实际上是与我们之前讨论的那样一样，是矩阵\(\mathbf A\)各列的线性组合，这联系了线性方程组的几何上的原理。

​ 第二种方法：

\[\begin{bmatrix} 2 & 5\\ 1 & 3 \end{bmatrix} \begin{bmatrix} 1\\ 2 \end{bmatrix} = \begin{bmatrix} 2\times 1 + 5\times 2\\ 1\times 1 + 3\times 2 \end{bmatrix} =\begin{bmatrix} 12\\ 7 \end{bmatrix} \]

这种解法实际上是线性方程组的定义式做法，即给未知数\(x\)和\(y\)赋值求得\(\mathbf b\)。