qiskit-metal学习第二步——学习参数

本文是在学习量子力学基础上，参考王腾辉论文以及qiskit-metal代码，学习关于代码中的一些参数值的含义、计算原理，尤其是电容的计算原理。

主要是了解以下的参数原理：

其中f_Q是量子比特频率。在非谐性条件下，以基态和次能级编码，|0>|1>之间的能级跃迁需要吸收光子，这里f_Q指光子的频率。

电感L和电容C并联构成LC谐振电路——体系的能量在静电能和磁场能之间来回振荡。

LC 谐振电路具备均匀的能级结构，相邻能级之间的能量差固定为 ℏωr。

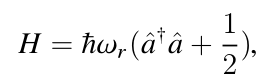
因此需要加入非线性元件——基于约瑟夫森结的超导量子比特。

约瑟夫森结伏安特性：

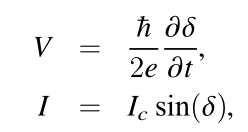
δ库珀对波函数相位差

V约瑟夫森结两端电压 、I约瑟夫森结流经电流

Ic临界电流

Lj约瑟夫森结的等效电感

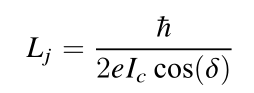
phi约瑟夫森结上的磁通

phi0=h/2e是磁通量子

相位差与磁通的关系：

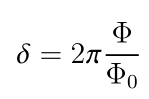
等效电感与磁通的关系：

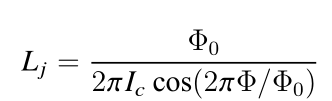
从而得知约瑟夫森结是一个非线性的电感元件，等效电感与磁通有关。

Ej约瑟夫森结能量：

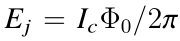
约瑟夫森结的哈密顿量是对功率的积分：

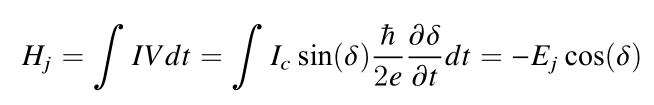
Ec单电子的电荷能量：

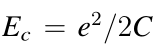
电路哈密顿量：

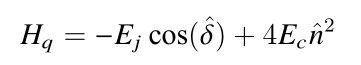
库珀对个数：

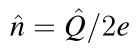
[phi,Q]对易，[n,δ]=i 共轭

升降算符还是不太理解

超导量子比特一般电路模型：

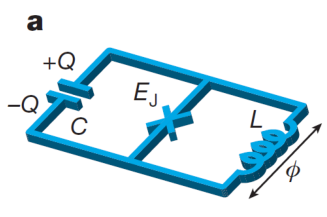
对电路哈密顿量做泰勒展开：

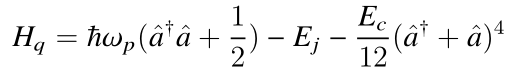
依照Ej/Ec划分量子比特种类：

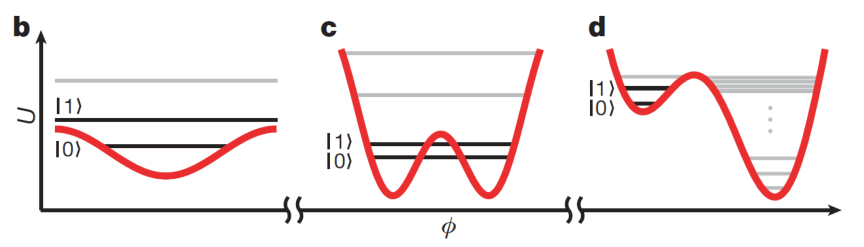
理论上不同的Ej/Ec会得到不同的能级分布，也对应了不同类型的超导量子比特。

b. Ej/Ec<<1 Ec大 电荷量子比特 charge qubit eg：transmon在此基础上增加Ej

c. Ej/Ec≈100 Ej大 磁通量子比特 flux qubit

d. Ej/Ec≈10000 Ej中等 相位量子比特 phase qubit

transmon的哈密顿量：

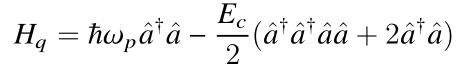
取最低两个能级编码为量子比特。

定义transmon|0>|1>与|1>|2>共振频率之差为非谐性alpha：

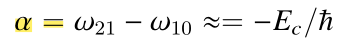
在超导量子比特中，比特的共振频率通常选取在 ω10/2π ≈ 4~6GHz, 比特的非谐性选取在 α/2π ≈ −200 ~ − 300 MHz。

简化的transmon量子比特哈密顿量：

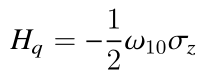
微波测量与耦合：

Cd 耦合电容

tCSq Pads之间的总电容

CJ 结电容

Cs qubit pads之间的电容

C1S与C2S分别表示为：qubit pad（1，2） 到ground_index与bus_index的耦合电容qubit pad1与qubit pad2是串联关系

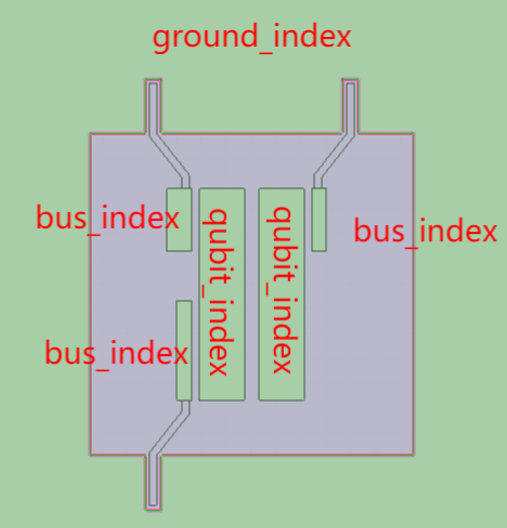
Cq = tCSq + CJ

tCSq = Cs + C1S * C2S / (C1S + C2S)

Cs = -capMatrix[qubit_index[0], qubit_index[1]]

C1S = Cg[0] + np.sum(Cbus[0,])

C2S = Cg[1] + np.sum(Cbus[1,])

参考qiskit-metal代码、王腾辉 《超导量子比特与绝热快速捷径在量子模拟和量子门中的应用》、以及何学长的讲解
[1]王腾辉. 超导量子比特与绝热快速捷径在量子模拟和量子门中的应用[D]. 浙江:浙江大学,2018.