基于Simulink的二阶系统频谱分析

基于Simulink的二阶系统频谱分析

软件：MATLAB、Solidworks、COMSOL

制作人：梦想小猪

制作时间：2023年6月12日

参考文献

[1] Ni Y, Li H, Huang L, et al. On bandwidth characteristics of tuning fork micro-gyroscope with mechanically coupled sense mode[J]. Sensors, 2014, 14(7): 13024-13045.

[2] Sheikhaleh A, Jafari K, Abedi K. Design and analysis of a novel MOEMS gyroscope using an electrostatic comb-drive actuator and an optical sensing system[J]. IEEE Sensors Journal, 2018, 19(1): 144-150.

问题描述

问题叙述

如何建立基于科氏效应的陀螺仪数学模型？如何分析其频率响应，计算灵敏度？

解决思路

（1）在COMSOL中建立驱动检测解耦的陀螺结构，并获取其质量、刚度等信息；

（2）联立驱动检测方向的“质量-弹簧-阻尼”系统动态方程；

其中驱动力，

方程根据牛顿第二定律构建，x轴为驱动方向，y轴为检测方向。其中是科氏力。

（3）根据（2）中的方程，在Simulink中搭建方程模块；

（4）采用MATLAB的实时编程功能进行频率响应的分析。

操作流程

双击打开MATLAB软件。

工具栏中左键单击Simulink，打开Simulink。

进入Simulink界面，在Library中选择需要使用到的模块。

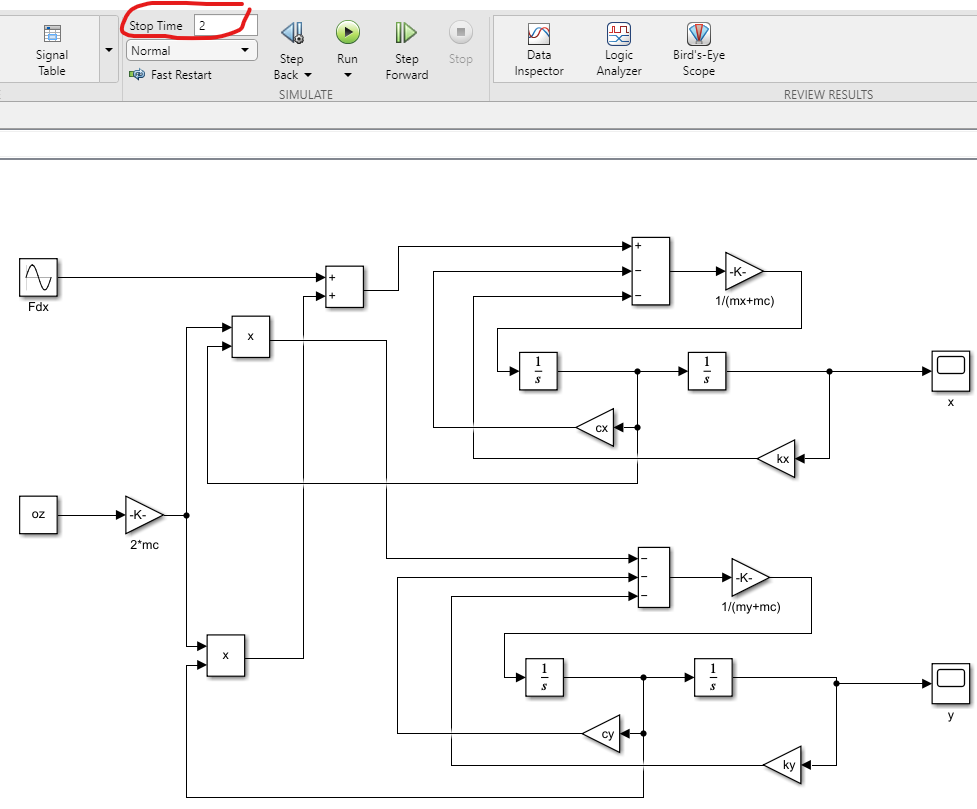
根据陀螺方程，在Simulink中搭建方程模块，如下图所示。

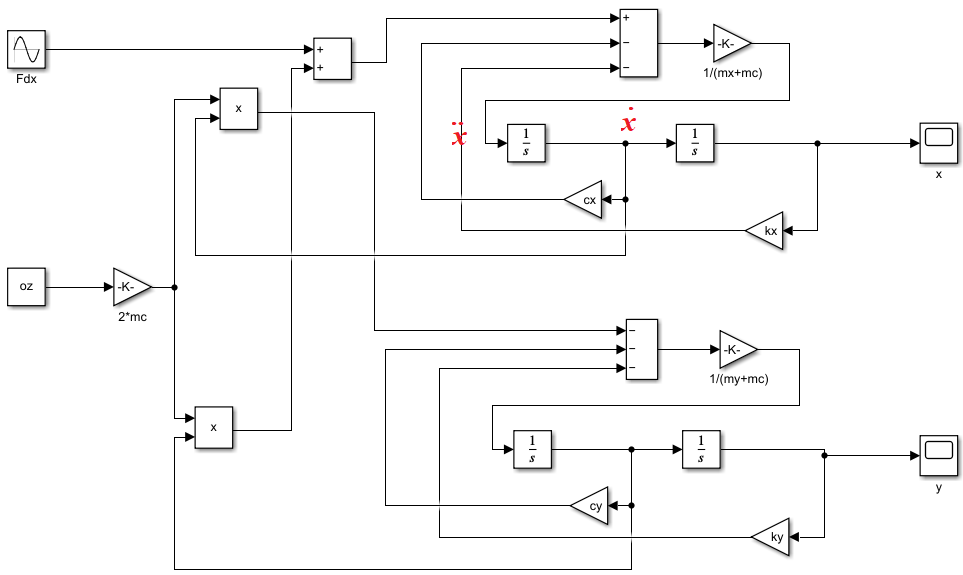
在MATLAB实时编辑器中定义参量：

%parameters;

mx = 0.8e-7; %kg，驱动解耦框质量

my = 0.8e-7; %kg，检测解耦框质量

mc = 0.5e-6; %kg，科氏质量

fx = 5480; %Hz，驱动模态的特征频率，由COMSOL仿真得到

fy = 5864; %Hz，检测模态的特征频率，由COMSOL仿真得到

kx = (mx+mc)*(2*pi*fx)^2; %N/m

ky = (my+mc)*(2*pi*fy)^2; %N/m

Qx= 1000;

Qy= 1000;

cx= (mx+mc)*(2*pi*fx)/Qx ; %N/(m/s)

cy= (my+mc)*(2*pi*fy)/Qy ; %N/(m/s)

oz= 100; %rad/s 输入角速率，手动扫描，后期分析灵敏度**

Fd= 10e-6; %N 驱动振幅

fd= 10 ; %Hz驱动频率，扫描参量

陀螺的机械模型

在COMSOL中建立陀螺的机械结构，并进行特征频率分析，具体参数参考文献[1]。

如何代入参数值？

k, c为等效刚度和等效阻尼。在MEMS系统中相对于内在阻尼（如热弹性阻尼、锚点损耗）空气阻尼占主导地位，在低真空封装下，Q值一般为1500，高真空封装下，Q值能达到20000。

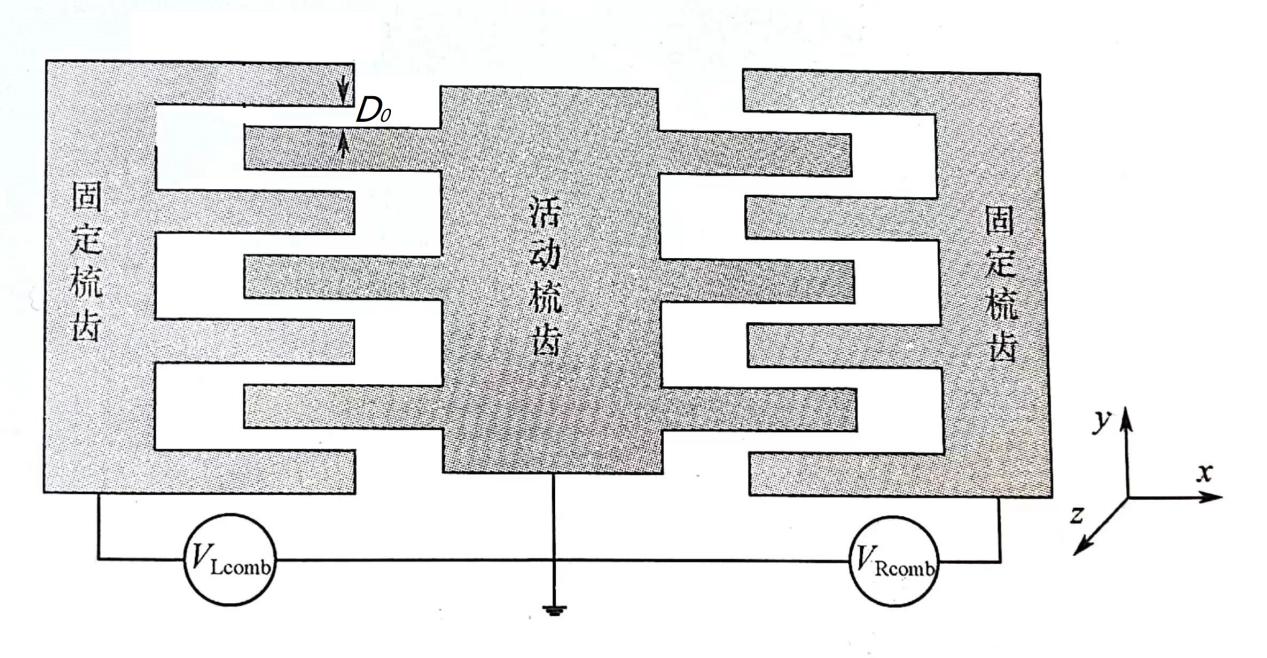
驱动振幅Fd的值如何计算？

其中，N梳齿个数，H₀梳齿厚度，D₀梳齿间隙，V₀直流分量，V₁交流分量幅度。

示波器显示时域波形

在MATLAB实时编辑器中定义好参量后，点击运行按钮，参数值就会代入Simulink模型。

运行Simulink模型：

双击示波器x，y分别查看位移随时间的变化：

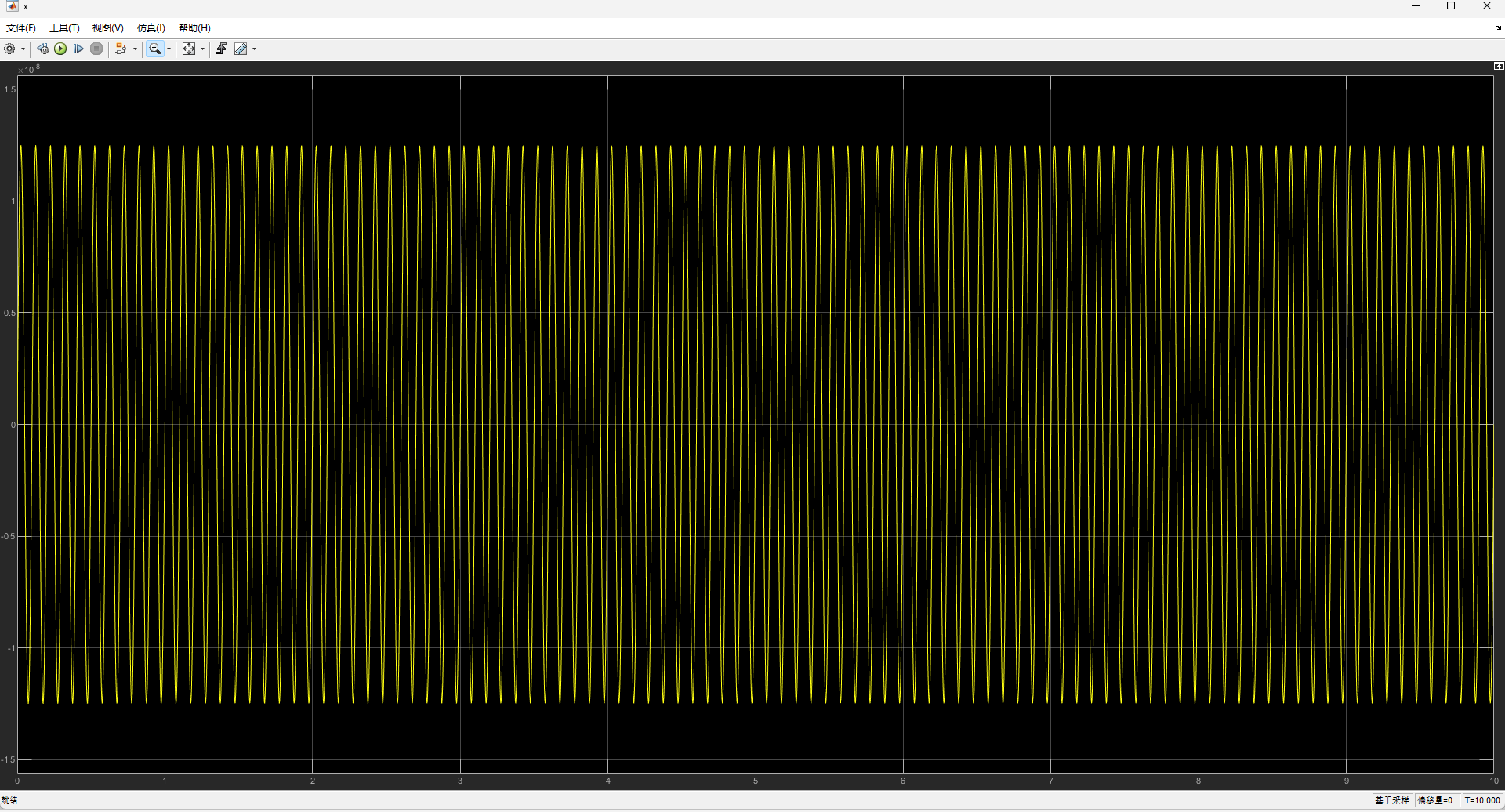
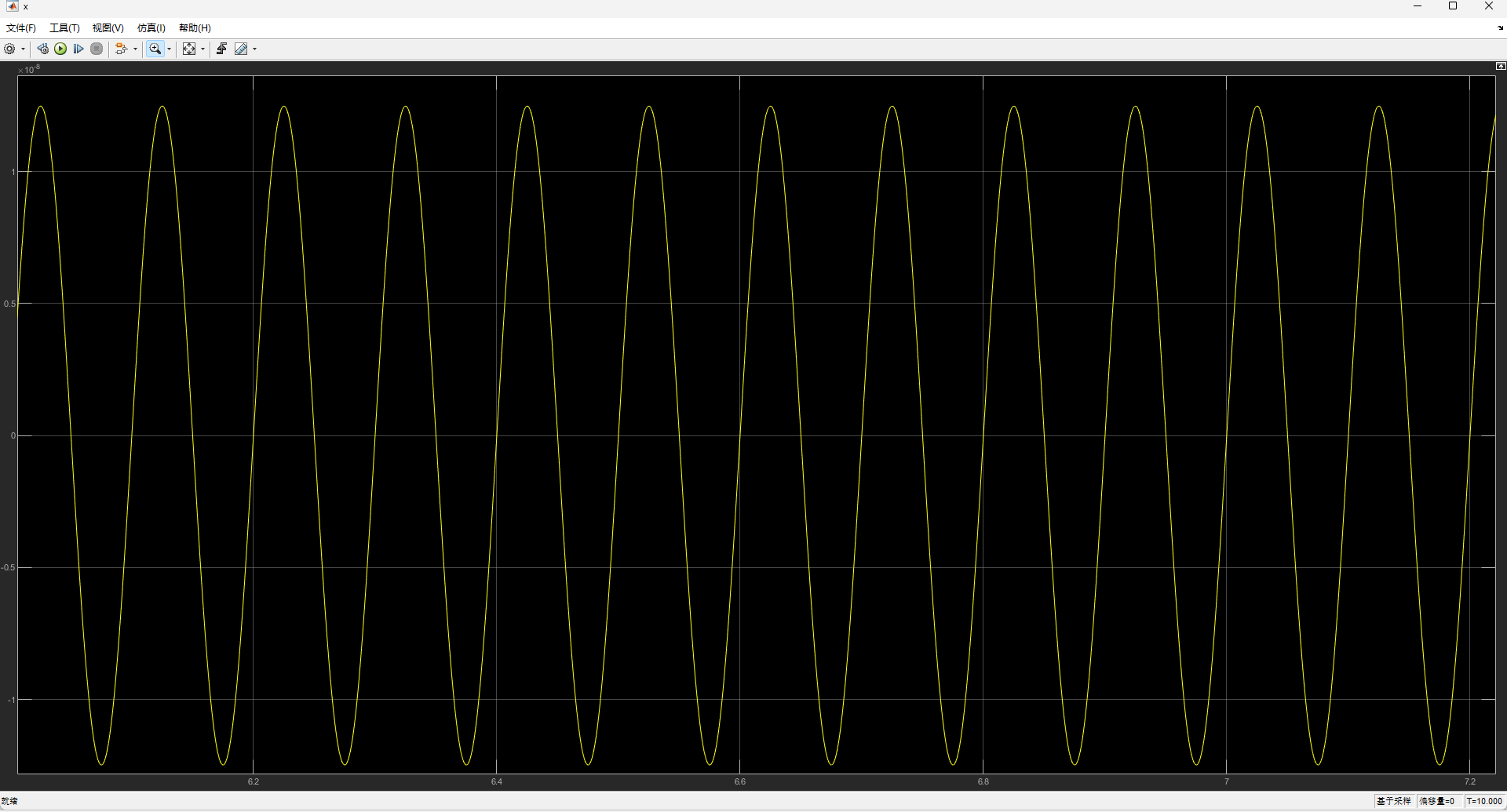
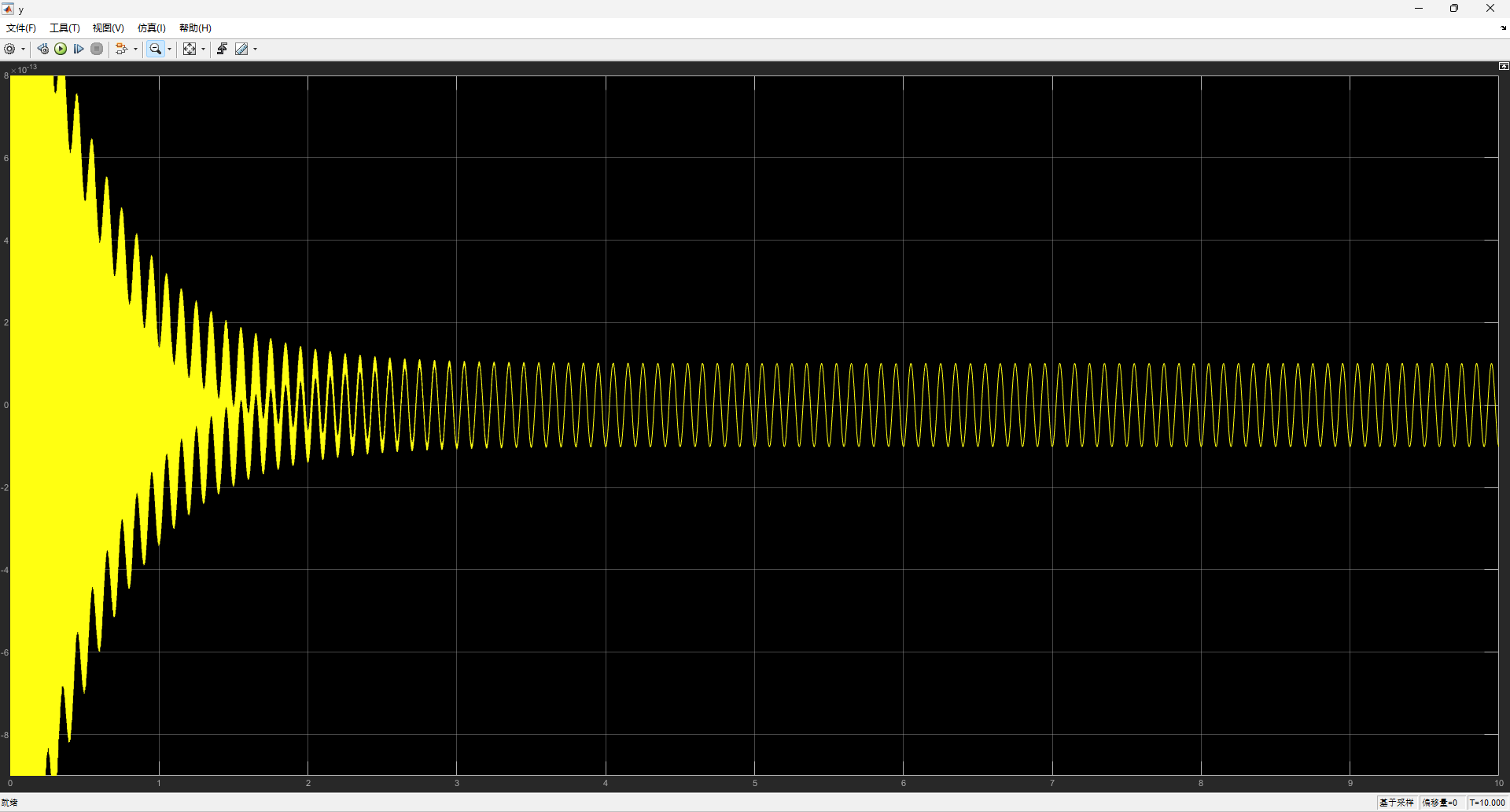
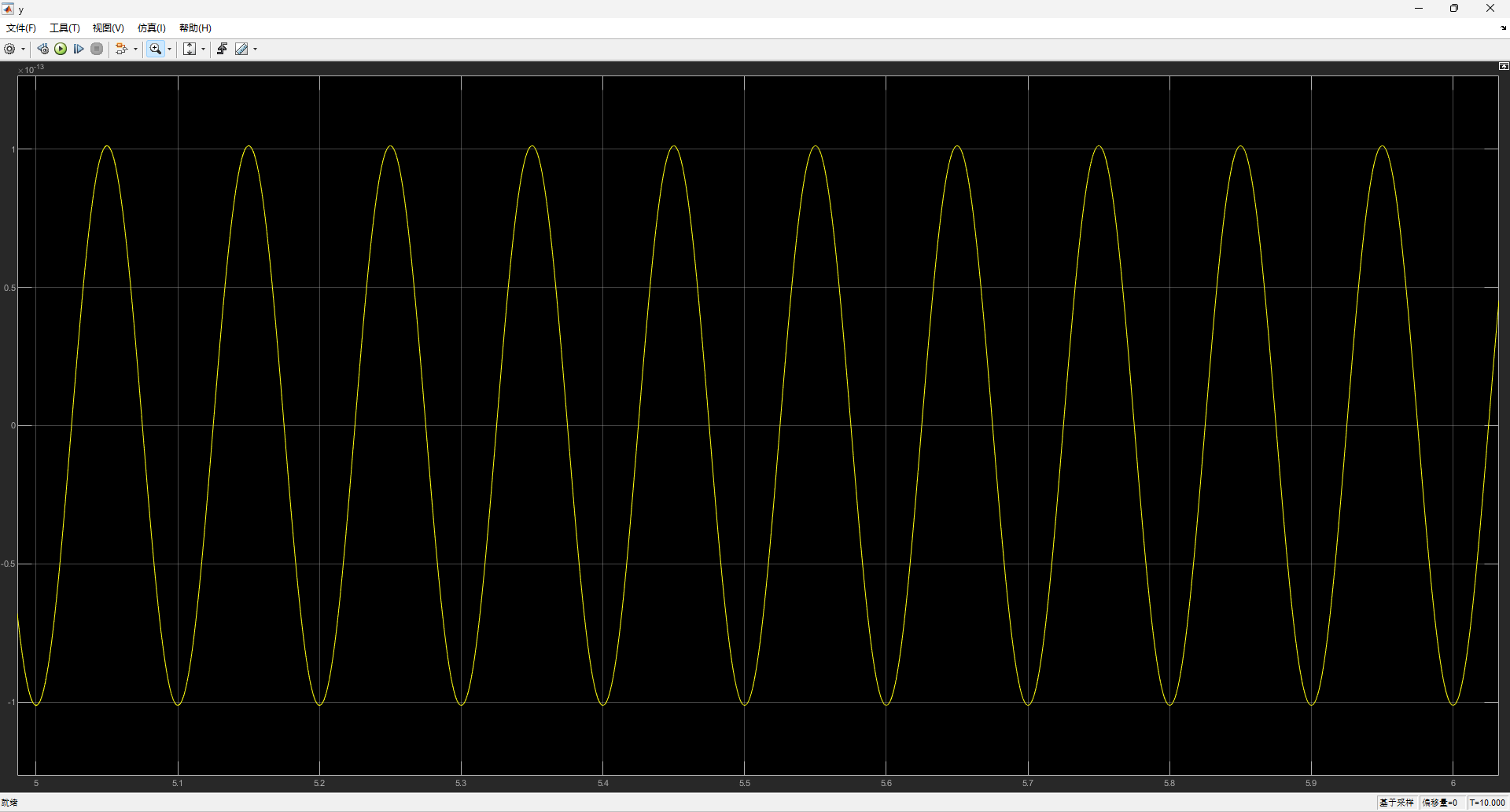
查看工作区中存储的参数及其数据类型，调用数据。

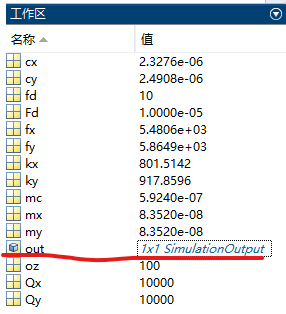
双击out查看仿真结果存储的数据内容：

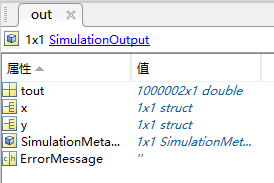
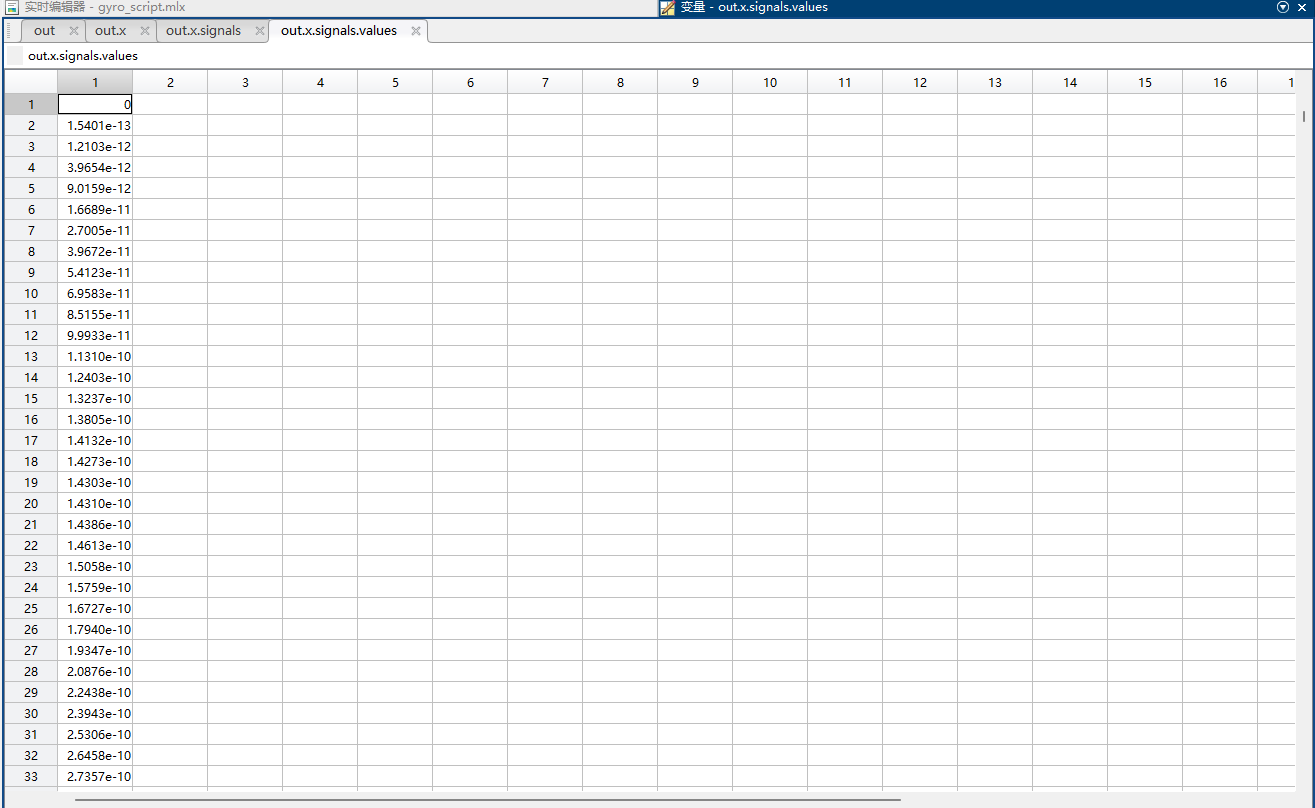
频率扫描

%frequency sweep

f_sweep = [0:100:10000, 5000:1:6000];

y_rms = zeros(size(f_sweep));

for i = 1:length(f_sweep)

fd = f_sweep(i);

sim("D:\zzy\23-1phc-gyro\matlab\gyro.slx");

t = out.y.time ;

y = out.y.signals.values ;

y_rms(i) = rms(y(t>1));

end

scatter(f_sweep,y_rms)

%frequency sweep

f_sweep = [0:100:10000, 5000:1:6000]; %建立一个矩阵f_sweep，设置扫描步长，f_sweep为行向量

y_rms = zeros(size(f_sweep)); %size语法获取数组的大小size(f_sweep)=(1,x)

% x为矩阵长度；zeros(*,*)需要行数和列数两个参数，创建全0矩阵。

%zeros(size(f_sweep))整体记忆，意味创建存储y_rms的全零行向量，长度和矩阵f_sweep一样。

for i = 1:length(f_sweep) %length返回值为行向量长度

fd = f_sweep(i); %MATLAB的索引是从1开始的，不是0，因此返回数组中第i个元素。

sim("D:\zzy\23-1phc-gyro\matlab\gyro.slx"); %运行一次simulink模型

t = out.y.time ;

y = out.y.signals.values ; %调用simulink仿真结果，时域的幅值。

y_rms(i) = rms(y(t>1)); %rms函数计算均方根

end

scatter(f_sweep,y_rms) %绘制散点图

仿真结果：

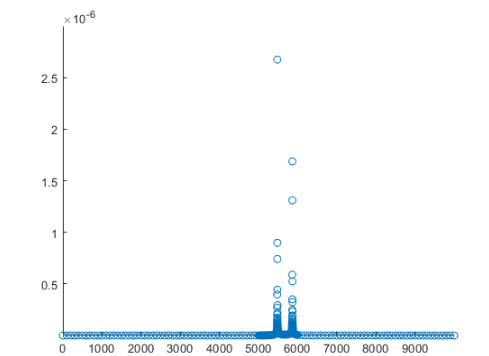
经验分享

（1）合理设置仿真步长，避免波形毛刺。最大步长设置为5e-5至5e-6可以保证仿真精度。合理设置求解器，避免波形振荡。本案例中因为含有积分器，仿真前期会出现振荡，需要仿真时间久一点，波形才会稳定下来。

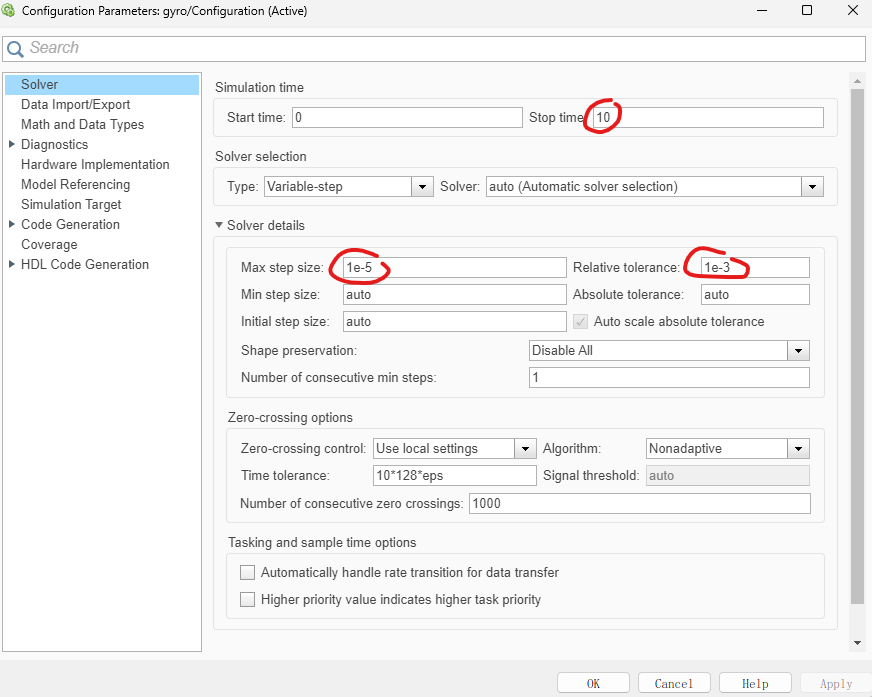
（2）MATLAB语法——for循环

基本语法：

for index = values

statements;

end

Index是循环变量，values是一个向量或矩阵，statements是重复执行语句块。循环变量index会从values中取出每个元素，依次执行statements语句块。

举例：打印1到5的整数

for i = 1:5

disp(i);

End

（3）去掉工作区模块out.前缀

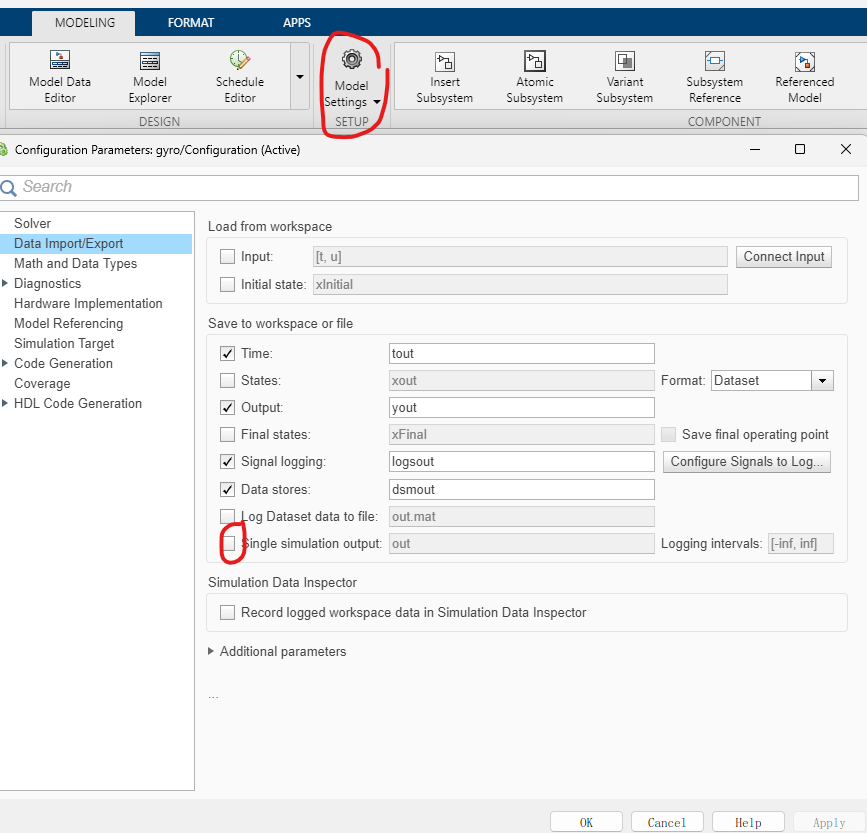
取消勾选single simulation output，工作区显示：

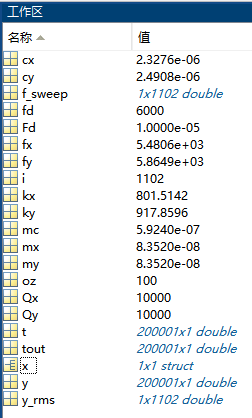
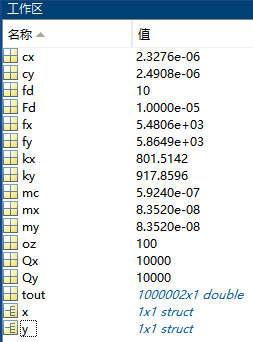便于直接调用数据，而不用加前缀out.

附录：完整代码

%parameters;

mx = 0.8e-6; %kg，驱动解耦框质量

my = 0.8e-6; %kg，检测解耦框质量

mc = 0.5e-6; %kg，科氏质量

fx = 5480; %Hz，驱动模态的特征频率，由COMSOL仿真得到

fy = 5864; %Hz，检测模态的特征频率，由COMSOL仿真得到

kx = (mx+mc)*(2*pi*fx)^2; %N/m

ky = (my+mc)*(2*pi*fy)^2; %N/m

Qx = 1000;

Qy = 1000;

cx = (mx+mc)*(2*pi*fx)/Qx ; %N/(m/s)

cy = (my+mc)*(2*pi*fy)/Qy ; %N/(m/s)

oz = 100; %rad/s 输入角速率，手动扫描，后期分析灵敏度**

Fd = 10e-6; %N 驱动振幅

fd = 10 ; %Hz驱动频率，扫描参量

%frequency sweep

f_sweep = [0:1000:10000, 5000:100:6000]; %建立一个矩阵f_sweep，设置扫描步长，f_sweep为行向量

y_rms = zeros(size(f_sweep)); %size语法获取数组的大小size(f_sweep)=(1,x)

% x为矩阵长度；zeros(*,*)需要行数和列数两个参数，创建全0矩阵。

%zeros(size(f_sweep))整体记忆，意味创建存储y_rms的全零行向量，长度和矩阵f_sweep一样。

for i = 1:length(f_sweep) %length返回值为行向量长度

fd = f_sweep(i); %MATLAB的索引是从1开始的，不是0，因此返回数组中第i个元素。

sim("D:\zzy\23-1phc-gyro\matlab\gyro.slx"); %运行一次simulink模型

t = y.time ;

y = y.signals.values ; %调用simulink仿真结果，时域的幅值。

y_rms(i) = rms(y(t>1)); %rms函数计算均方根

end

scatter(f_sweep,y_rms) %绘制散点图