神仙题2.0

「JOISC 2020 Day1」扫除

题目链接

先不考虑加点.

那么一个\(H\)操作影响的范围是\((x,n - l]\)

\(x\)是在这个\(H\)操作之前的\(V\)操作所影响的最大的横坐标

\(V\)操作类似

画个图理解一下大概就是:

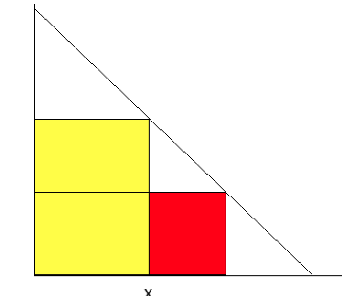
红色部分为\(H\)可以影响的范围(黄色的部分灰尘被移出去了)
然后这个可以通过线段树来维护.

考虑有加点,我们可以使用线段树分治
一个点的询问可以看做使用了他出现的时间到询问的时间这段时间的操作
然后一段一段区间对它贡献,这样就没有插入操作了.

最大的问题就是操作之间的影响.
我们通过上述的方法可以算出每个区间影响的范围,然后惊讶的发现
操作\(H\)和\(V\)似乎不会相互影响了?感性理解一下
这样我们就可以分开计算x,y的变化

#include <bits/stdc++.h>
#define LL long long
#define RG register
using namespace std;
template <class T>
T gi() {
    T x = 0;
    bool f = 0;
    char c = getchar();
    while (c != '-' && (c < '0' || c > '9')) c = getchar();
    if (c == '-')
        f = 1, c = getchar();
    while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
    return f ? -x : x;
}
const int N = 1e6 + 10;
namespace sgt {
	int rt[2], tot, ls[N * 40], rs[N * 40], mx[N * 40];
	void clear() { rt[0] = rt[1] = tot = 0; }
	void upd(int &o, int l, int r, int L, int R, int x) {
		if (!o)
			o = ++tot, ls[o] = rs[o] = mx[o] = 0;
		if (L <= l && r <= R)
			return (void)(mx[o] = max(mx[o], x));
		int mid = (l + r) >> 1;
		if (L <= mid)
			upd(ls[o], l, mid, L, R, x);
		if (R > mid)
			upd(rs[o], mid + 1, r, L, R, x);
	}
	int qry(int o, int l, int r, int p) {
		if (!o)
			return 0;
		if (l == r)
			return mx[o];
		int mid = (l + r) >> 1;
		if (p <= mid)
			return max(mx[o], qry(ls[o], l, mid, p));
		return max(mx[o], qry(rs[o], mid + 1, r, p));
	}
}; 
using namespace sgt;
int n, m, q, tp[N], len[N], ansx[N], ansy[N], ql[N], qr[N], X[N], Y[N], t[N];
vector<pair<int, int> > opt[2];
void pre(int x) {
    opt[tp[x]].emplace_back(len[x], qry(rt[tp[x] ^ 1], 0, n, len[x]));
    upd(rt[tp[x]], 0, n, opt[tp[x]].back().second, n - len[x] - 1, len[x] + 1);
}
bool cmpx(int x, int y) { return ansx[x] > ansx[y]; }
bool cmpy(int x, int y) { return ansy[x] > ansy[y]; }
void solve(int l, int r, vector<int> q) {
    if (q.empty())
        return;
    int mid = (l + r) >> 1;
    vector<int> lq, rq, now;
    clear();
    opt[0].clear();
    opt[1].clear();
    for (int i = l; i <= r; i++) pre(i);
    clear();
    for (auto i : q)
        if (ql[i] <= l && qr[i] >= r)
            now.push_back(i);
        else {
            if (ql[i] <= mid)
                lq.push_back(i);
            if (qr[i] > mid)
                rq.push_back(i);
        }
    sort(opt[0].begin(), opt[0].end(), greater<pair<int, int> >());
    sort(now.begin(), now.end(), cmpy);
    int j = 0;
    for (auto i : now) {
        for (; j < opt[0].size() && opt[0][j].first >= ansy[i]; j++)
            upd(rt[0], 0, n, opt[0][j].second, n - opt[0][j].first, n - opt[0][j].first);
        ansx[i] = max(ansx[i], qry(rt[0], 0, n, ansx[i]));
    }
    sort(opt[1].begin(), opt[1].end(), greater<pair<int, int> >());
    sort(now.begin(), now.end(), cmpx);
    j = 0;
    for (auto i : now) {
        for (; j < opt[1].size() && opt[1][j].first >= ansx[i]; j++)
            upd(rt[1], 0, n, opt[1][j].second, n - opt[1][j].first, n - opt[1][j].first);
        ansy[i] = max(ansy[i], qry(rt[1], 0, n, ansy[i]));
    }
    solve(l, mid, lq);
    solve(mid + 1, r, rq);
    return;
}
int main() {
    freopen("in.in", "r", stdin);
    freopen("out.out", "w", stdout);
    n = gi<int>(), m = gi<int>(), q = gi<int>();
    int cnt = 0, cntq = 0;
    for (int i = 1; i <= m; i++) X[i] = gi<int>(), Y[i] = gi<int>(), t[i] = 1;
    for (int i = 1; i <= q; i++) {
        int op = gi<int>(), x = gi<int>();
        if (op == 1)
            ql[++cntq] = t[x], qr[cntq] = cnt, ansx[cntq] = X[x], ansy[cntq] = Y[x];
        if (op == 2)
            tp[++cnt] = 0, len[cnt] = x;
        if (op == 3)
            tp[++cnt] = 1, len[cnt] = x;
        if (op == 4)
            X[++m] = x, Y[m] = gi<int>(), t[m] = cnt + 1;
    }
    vector<int> q;
    for (int i = 1; i <= cntq; i++)
        if (ql[i] <= qr[i])
            q.push_back(i);
    solve(1, cnt, q);
    for (int i = 1; i <= cntq; i++) printf("%d %d\n", ansx[i], ansy[i]);
    return 0;
}