树论1
作者的题单本身叫“简单树论”,但是这里把“简单”隐去了。
kruskal 重构树
在做 kruskal 生成树时,我们将边权从小到大排序,若 \((u,v)\) 不连通,则加入这条边。
这个过程比较特别,考虑用一些结构来记录这个过程,于是有了 kruskal 重构树。
考虑每次加入一条边 \((u,v)\) 时,新建一个点 \(cnt\),连接到 \(fa_u\) 和 \(fa_v\),其中 \(fa\) 为并查集中 \(find\) 的结果。\(cnt\) 的点权为设置这条边的边权。
int find(int x){
return fa[x]==x?x:fa[x]=find(fa[x]);
}void merge(int u,int v,int w){
if((u=find(u))==(v=find(v)))
return;
a[++cnt]=w;fa[u]=fa[v]=cnt;
e[cnt].pb(u);e[cnt].pb(v);
siz[cnt]=siz[u]+siz[v];
}
考虑这棵树有什么性质。
- 如果整个图联通,则这是一棵整的树而不是树林,且这棵树又 \(2n-1\) 个节点。
- 二叉树。每个点要么有两个儿子要么自己就是叶子。
- 叶子节点是初始的 \(n\) 个节点,其余都是后加的。
- 任意非叶结点有 \(w_u\le w_{fa_u}\)。
由于最后一条性质,我们可以得出其关于原图的一条性质:
当我们从点 \(u\) 只走边权 \(\le d\) 的边时,能走到的点为重构树上 \(u\) 所有点权 \(\le d\) 的祖先的子树内所有点。而这个最高的结点,我们通常使用倍增去寻找。
因此,当题目出现只走边权不大于(不小于)某个值时我们便可以从 kruskal 重构树的方向考虑。
如果题目给的是点权,要求经过的点权 \(\le d\) 之类,可以将 \((u,v)\) 这条边的边权设置为 \(\max(w_u,w_v)\) 或是 \(\min(w_u,w_v)\),以此实现转化,具体因题而异。
CF1706E Qpwoeirut and Vertices
将一条边的边权设为其编号,建成大根 kruskal 重构树,于是每次询问便是在 kruskal重构树上求 \(w_{lca(l,l+1,...,r-1,r)}\)。
上面的值等价与 \(\max_{i=l}^{r-1}w_{lca(i,i+1)}\),因为使 \([l,r]\) 的点全部联通等价于使所有点 \(i\) 和 \(i+1\) 联通,\(i\in[l,r]\),于是就可以使用 ST 表维护。
#include<bits/stdc++.h>
using namespace std;
const int N=4e5+5;
int t,n,m,q;
int fa[N],val[N],cnt;
int head[N],to[N],nxt[N],tot;
int f[N][20],dep[N];
int find(int x){
return (fa[x]==x?x:fa[x]=find(fa[x]));
}
void add(int u,int v){
to[++tot]=v,nxt[tot]=head[u],head[u]=tot;
}
void merge(int u,int v,int w){
if((u=find(u))==(v=find(v)))return;
val[++cnt]=w;
fa[u]=fa[v]=cnt;
add(cnt,u),add(cnt,v);
}
void dfs(int u){
for(int i=1;i<=19;++i)
f[u][i]=f[f[u][i-1]][i-1];
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
f[v][0]=u,dep[v]=dep[u]+1,dfs(v);
}
}
int lca(int u,int v){
if(dep[u]<dep[v])swap(u,v);
for(int i=19;i>=0;--i)
if(dep[f[u][i]]>=dep[v])
u=f[u][i];
if(u==v)return u;
for(int i=19;i>=0;--i)
if(f[u][i]!=f[v][i])
u=f[u][i],v=f[v][i];
return f[u][0];
}
int ans[N][19];
int ask(int l,int r){
int k=log2(r-l+1);
return max(ans[l][k],ans[r-(1<<k)+1][k]);
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>t;
while(t--){
cin>>n>>m>>q;cnt=n;tot=0;
for(int i=1;i<=(n<<1);++i){
fa[i]=i,head[i]=val[i]=0;
for(int j=0;j<18;++j)
f[i][j]=0;
}
for(int i=1,u,v;i<=m;++i)
cin>>u>>v,merge(u,v,i);
dfs(cnt);
for(int i=1;i<n;++i)
ans[i][0]=val[lca(i,i+1)];
for(int j=1;j<=19;++j)
for(int i=1;i+(1<<j)-1<n;++i)
ans[i][j]=max(ans[i][j-1],ans[i+(1<<(j-1))][j-1]);
while(q--){
int x,y;cin>>x>>y;
if(x==y)cout<<"0 ";
else cout<<ask(x,y-1)<<' ';
}cout<<'\n';
}
return 0;
}
CF1628E Groceries in Meteor Town
考虑我们怎么快速查询。简单路径上经过的边,最大可能的权,说白了就是路径上的最大边权,这个我们可以用 kruskal 轻松维护。对于一个点与所有白点的答案最大值,我们只用求出所有白点的 lca 再和点 \(x\) 求一个 lca。
如何维护一群点的 lca。只需要找出其中 dfs 序的最大和最小值的点求一个 lca 就行。现在我们要维护白点中 dfn 的最大和最小值,考虑用线段树。
对于删除,若区间被完全覆盖,直接赋值 INF 和 -INF 并改标记就行。
对于添加,若区间被完全覆盖,直接赋值为预处理出的区间 dfn 最大和最小值并改标记就行。
#include<bits/stdc++.h>
using namespace std;
const int N=6e5+5,INF=0x3f3f3f3f;
struct edge{int u,v,w;}e[N];
bool cmp(edge x,edge y){
return x.w<y.w;
}
int n,q;
int fa[N],val[N],cnt;
int head[N],to[N],nxt[N],tot;
int find(int x){
return (fa[x]==x?x:fa[x]=find(fa[x]));
}
void add(int u,int v){
nxt[++tot]=head[u],head[u]=tot,to[tot]=v;
}
void merge(int u,int v,int w){
u=find(u),v=find(v);
val[++cnt]=w;
fa[u]=fa[v]=cnt;
add(cnt,u),add(cnt,v);
}
int dep[N],f[N][21];
int dfn[N],nfd[N],timen;
void dfs(int u){
nfd[dfn[u]=++timen]=u;
for(int i=1;i<=20;++i)
f[u][i]=f[f[u][i-1]][i-1];
for(int i=head[u];i;i=nxt[i])
dep[to[i]]=dep[u]+1,f[to[i]][0]=u,dfs(to[i]);
}
int lca(int u,int v){
if(dep[u]<dep[v])swap(u,v);
for(int i=20;i>=0;--i)
if(dep[f[u][i]]>=dep[v])
u=f[u][i];
if(u==v)return u;
for(int i=20;i>=0;--i)
if(f[u][i]!=f[v][i])
u=f[u][i],v=f[v][i];
return f[u][0];
}
#define ls(p) (p<<1)
#define rs(p) (p<<1|1)
#define mid ((l+r)>>1)
int tag[N<<3],ans[N<<3][2],res[N<<3][2];
void push_up(int p){
ans[p][0]=max(ans[ls(p)][0],ans[rs(p)][0]);
ans[p][1]=min(ans[ls(p)][1],ans[rs(p)][1]);
res[p][0]=max(res[ls(p)][0],res[rs(p)][0]);
res[p][1]=min(res[ls(p)][1],res[rs(p)][1]);
}
void push_down(int p){
if(tag[p]==1){
tag[ls(p)]=tag[rs(p)]=1;
res[ls(p)][0]=ans[ls(p)][0];
res[ls(p)][1]=ans[ls(p)][1];
res[rs(p)][0]=ans[rs(p)][0];
res[rs(p)][1]=ans[rs(p)][1];
}
if(tag[p]==2){
tag[ls(p)]=tag[rs(p)]=2;
res[ls(p)][0]=res[rs(p)][0]=-INF;
res[ls(p)][1]=res[rs(p)][1]=INF;
}
tag[p]=0;
}
void build(int p,int l,int r){
if(l==r){
tag[p]=0;
ans[p][0]=ans[p][1]=dfn[l];
res[p][0]=-INF,res[p][1]=INF;
return;
}
build(ls(p),l,mid);
build(rs(p),mid+1,r);
push_up(p);
}
void update(int p,int l,int r,int L,int R,int op){
if(L<=l&&r<=R){
tag[p]=op;
if(op==1)res[p][0]=ans[p][0],res[p][1]=ans[p][1];
else res[p][0]=-INF,res[p][1]=INF;
return;
}
push_down(p);
if(L<=mid)update(ls(p),l,mid,L,R,op);
if(mid<R)update(rs(p),mid+1,r,L,R,op);
push_up(p);
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>q;cnt=n;
for(int i=1;i<=(n<<1);++i)
fa[i]=i;
for(int i=1,u,v,w;i<n;++i)
cin>>e[i].u>>e[i].v>>e[i].w;
sort(e+1,e+n,cmp);
for(int i=1;i<n;++i)
merge(e[i].u,e[i].v,e[i].w);
dep[cnt]=1,dfs(cnt);
build(1,1,n);
while(q--){
int op,x,y;
cin>>op>>x;
if(op<3)cin>>y,update(1,1,n,x,y,op);
else{
int s=res[1][0],t=res[1][1],ans=-1;
s=max(s,dfn[x]),t=min(t,dfn[x]);
if(s!=t){
y=lca(nfd[s],nfd[t]);
if(x!=y)ans=val[y];
}
cout<<ans<<'\n';
}
}
return 0;
}
P4899 [IOI2018] werewolf 狼人
多次询问是否存在一条 \(s\to t\) 的路径,其前一段只走编号大于等于 \(L\) 的点,后一段只走编号小于等于 \(R\) 的点。
题面很显然想到重构树。
我们将点权转到边权,也就是上面讲过的方式,建出两棵重构树,一棵能找出编号 \(\le R\) 的点,一棵能找出编号 \(\ge L\) 的点。
现在就是两棵树各选出一个子树,判断其中是否有交,即变身的位置。考虑两个排列各取一段区间怎么做,将 \(b_i\) 变为 \(b_i\) 再 \(a\) 中出现的位置,现在判断是否有 \(l_a\le b_i\le r_a,l_b\le i\le r_b\),就可以用主席树做二维数点了,在树上将 \(l,r\) 换成 dfs 序就可以了。
在线是用主席树,离线就可以用树状数组了。
#include<bits/stdc++.h>
#define pb push_back
#define mid (l+r>>1)
using namespace std;
const int N=4e5+5,M=6e6+5;
int n,m,q,gty[N];
struct edge{int u,v;}e[N];
struct tree{
int fa[N],f[N][20];
int dfn[N],nfd[N],val[N],cnt,tim;
int to[N];
vector<int> g[N];
int find(int x){
return fa[x]==x?x:fa[x]=find(fa[x]);
}void merge(int u,int v,int w){
if((u=find(u))==(v=find(v)))
return;
val[++cnt]=w;fa[u]=fa[v]=cnt;
g[cnt].pb(u);g[cnt].pb(v);
}void dfs(int u){
for(int i=1;i<=19;++i)
f[u][i]=f[f[u][i-1]][i-1];
if(u<=n)to[dfn[u]=++tim]=val[u]=u;
else dfn[u]=tim+1;
for(int v:g[u])f[v][0]=u,dfs(v);
nfd[u]=tim;
}int find(int u,int v,int t){
if(t){
for(int i=19;i>=0;--i)
if(val[f[u][i]]<=v)
u=f[u][i];
}else{
for(int i=19;i>=0;--i)
if(val[f[u][i]]>=v)
u=f[u][i];
}return u;
}
}t1,t2;
int rt[N],tot;
struct node{int ls,rs,w;}a[10000000];
void update(int &p,int lp,int l,int r,int x){
a[p=++tot]=a[lp];++a[p].w;
if(l==r)return;
if(x<=mid)update(a[p].ls,a[lp].ls,l,mid,x);
else update(a[p].rs,a[lp].rs,mid+1,r,x);
}int query(int p,int q,int l,int r,int L,int R,int res=0){
if(L<=l&&r<=R)return a[p].w-a[q].w;
if(L<=mid)res+=query(a[p].ls,a[q].ls,l,mid,L,R);
if(mid<R)res+=query(a[p].rs,a[q].rs,mid+1,r,L,R);
return res;
}bool cmp1(edge x,edge y){
return min(x.u,x.v)>min(y.u,y.v);
}bool cmp2(edge x,edge y){
return max(x.u,x.v)<max(y.u,y.v);
}signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>m>>q;t1.cnt=t2.cnt=n;
for(int i=1;i<=n*2;++i)
t1.fa[i]=t2.fa[i]=i;
for(int i=1;i<=m;++i)
cin>>e[i].u>>e[i].v,++e[i].u,++e[i].v;
sort(e+1,e+m+1,cmp1);
for(int i=1;i<=m;++i)
t1.merge(e[i].u,e[i].v,min(e[i].u,e[i].v));
sort(e+1,e+m+1,cmp2);
for(int i=1;i<=m;++i)
t2.merge(e[i].u,e[i].v,max(e[i].u,e[i].v));
t1.f[t1.cnt][0]=t1.cnt;
t2.f[t2.cnt][0]=t2.cnt;
t1.dfs(t1.cnt),t2.dfs(t2.cnt);
for(int i=1;i<=n;++i)
gty[t1.to[i]]=i;
for(int i=1;i<=n;++i)
update(rt[i],rt[i-1],1,n,gty[t2.to[i]]);
while(q--){
int s,t,l,r;
cin>>s>>t>>l>>r;
++s,++t,++l,++r;
int x=t1.find(s,l,0),y=t2.find(t,r,1);
cout<<(query(rt[t2.nfd[y]],rt[t2.dfn[y]-1],1,n,t1.dfn[x],t1.nfd[x])>0?1:0)<<'\n';
}
return 0;
}
P7834 [ONTAK2010] Peaks 加强版
权值小于等于 \(x\) 这个太明显了,直接上重构树,然后用 dfs 序加主席树维护子树第 \(k\) 大就好了。
#include<bits/stdc++.h>
#define lnt long long
#define pb push_back
using namespace std;
const int N=1e6+5,M=1e7;
int n,m,q,a[N];
int cnt,tot,tim,lans;
int siz[N],fa[N];
int rt[N],f[N][20];
int dfn[N],nfd[N];
vector<int> e[N];
struct edge{int u,v,w;}b[N];
struct node{int ls,rs,w;}c[M];
bool cmp(edge x,edge y){return x.w<y.w;}
int find(int x){
return fa[x]==x?x:fa[x]=find(fa[x]);
}void merge(int u,int v,int w){
if((u=find(u))==(v=find(v)))
return;
a[++cnt]=w;fa[u]=fa[v]=cnt;
e[cnt].pb(u);e[cnt].pb(v);
siz[cnt]=siz[u]+siz[v];
}void update(int &p,int lp,int l,int r,int x){
c[p=++tot]=c[lp];++c[p].w;
if(l==r)return;int mid=l+r>>1;
if(x<=mid)update(c[p].ls,c[lp].ls,l,mid,x);
else update(c[p].rs,c[lp].rs,mid+1,r,x);
}int query(int p,int q,int l,int r,int k){
if(l==r)return l;
int mid=(l+r)/2,gty=c[c[p].rs].w-c[c[q].rs].w;
if(k<=gty)return query(c[p].rs,c[q].rs,mid+1,r,k);
return query(c[p].ls,c[q].ls,l,mid,k-gty);
}void dfs(int u){
for(int i=1;i<=19;++i)
f[u][i]=f[f[u][i-1]][i-1];
if(u>n){
dfn[u]=++tim;
rt[tim]=rt[tim-1];
for(int v:e[u])
f[v][0]=u,dfs(v);
nfd[u]=tim;
}else{
dfn[u]=nfd[u]=++tim;
update(rt[tim],rt[tim-1],0,1000000001,a[u]);
}
}signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>m>>q;cnt=n;
for(int i=1;i<=n*2;++i)
fa[i]=i;
for(int i=1;i<=n;++i)
cin>>a[i],siz[i]=1;
for(int i=1;i<=m;++i)
cin>>b[i].u>>b[i].v>>b[i].w;
sort(b+1,b+m+1,cmp);
for(int i=1;i<=m;++i)
merge(b[i].u,b[i].v,b[i].w);
for(int i=n+1;i<=cnt;++i)
if(fa[i]==i)
f[i][0]=i,dfs(i);
while(q--){
int u,x,k;
cin>>u>>x>>k;
u=(u^lans)%n+1;
k=(k^lans)%n+1;
x=(x^lans);
for(int i=19;i>=0;--i)
if(a[f[u][i]]<=x)
u=f[u][i];
if(siz[u]<k)lans=0,cout<<-1<<'\n';
else cout<<(lans=query(rt[nfd[u]],rt[dfn[u]-1],0,1000000001,k))<<'\n';
}
return 0;
}
虚树
P2495 [SDOI2011] 消耗战
如果暴力 DP,有 \(f_u=\sum_{v\in son(u)}\min(f_v,w_{(u,v)})\),这样复杂度是 \(O(n)\) 的,无法应对多次询问。
我们发现,题目每次给一个点集,总点数不是很多,因此大多数 DP 转移是无意义的。其实可以将两个关键点之间的链使用一条权为上面的最小值的边代替。
例如左边的树(红色为关键点)建虚树长右边这样。
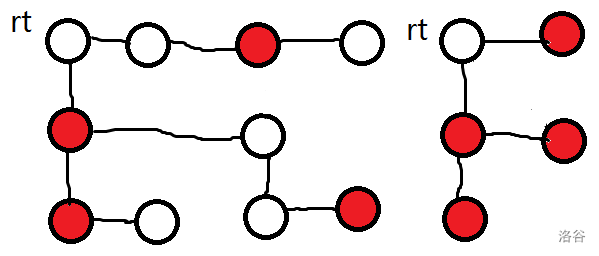
这里作者不想为了小常数去将单调栈的做法。将每个关键点按照 dfs 排序,相邻两个点加入一个 lca,然后去重后重加就够了,复杂度 \(O(k\log k)\),其实与单调栈复杂度一样,题目再卡常也不能卡正解罢。
正确性说一下。考虑相邻两个点 \(x,y\)。
- 如果 \(x\) 是 \(y\) 的祖先,那么连起来刚好。
- 如果 \(x\) 不是 \(y\) 的祖先,那么这样是把 \(x,y\) 沟通起来,最后形成一棵树。
感性理解一下即可。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=250005,INF=1e17;
int n,m,k;
int head[N],Head[N],tot,Tot;
int f[N][21],dep[N],dfn[N],cnt;
int minn[N];
vector<int> q;
bool isq[N];
struct edge{int v,w,nxt;}e[N<<1],E[N<<1];
void add(int u,int v,int w){
e[++tot]=(edge){v,w,head[u]},head[u]=tot;
}void Add(int u,int v){
E[++Tot]=(edge){v,0,Head[u]},Head[u]=Tot;
}void dfs(int u){
dfn[u]=++cnt;
for(int i=1;i<=20;++i)
f[u][i]=f[f[u][i-1]][i-1];
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(v==f[u][0])continue;
dep[v]=dep[u]+1,f[v][0]=u;
minn[v]=min(minn[u],e[i].w);
dfs(v);
}
}int Dfs(int u){
int sum=0,ans=minn[u];
for(int i=Head[u];i;i=E[i].nxt)
sum+=Dfs(E[i].v);
if(!isq[u])ans=min(ans,sum);
isq[u]=Head[u]=0;
return ans;
}int lca(int u,int v){
if(dep[u]<dep[v])swap(u,v);
for(int i=20;i>=0;--i)
if(dep[f[u][i]]>=dep[v])
u=f[u][i];
if(u==v)return u;
for(int i=20;i>=0;--i)
if(f[u][i]!=f[v][i])
u=f[u][i],v=f[v][i];
return f[u][0];
}bool cmp(int u,int v){return dfn[u]<dfn[v];}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1,u,v,w;i<n;++i)
cin>>u>>v>>w,add(u,v,w),add(v,u,w);
minn[1]=INF;
dep[1]=1,dfs(1);
cin>>m;
while(m--){
cin>>k;
for(int i=1,x;i<=k;++i)
cin>>x,q.push_back(x),isq[x]=1;
sort(q.begin(),q.end(),cmp);
for(int i=0;i<k-1;++i)
q.push_back(lca(q[i],q[i+1]));
q.push_back(1);
sort(q.begin(),q.end());
q.erase(unique(q.begin(),q.end()),q.end());
sort(q.begin(),q.end(),cmp);
for(int i=0;i<(int)q.size()-1;++i)
Add(lca(q[i],q[i+1]),q[i+1]);
cout<<Dfs(q[0])<<'\n';
Tot=0;q.clear();
}
return 0;
}
P4103 [HEOI2014] 大工程
对于第一问,一条边 \((u,v)\) 的贡献为 \(w_{u,v}\times siz_v(k-siz_v)\),在虚树过程中记录 \(siz\) 即可。
对于第二和第三问,维护字数内最长(最短)到达根的链,然和考虑拼接即可。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+5,INF=1e17;
int n,m,k;
int head[N],tot;
int Head[N],Tot;
int f[N][21],dep[N],dfn[N],cnt;
int ans1,ans2,ans3;
int siz[N],f1[N],f2[N];
struct edge{int v,nxt;}e[N<<1],E[N<<1];
void add(int u,int v){
e[++tot]=(edge){v,head[u]},head[u]=tot;
}void Add(int u,int v){
E[++Tot]=(edge){v,Head[u]},Head[u]=Tot;
}vector<int> q;
bool isq[N];
void dfs(int u){
dfn[u]=++cnt;
for(int i=1;i<=20;++i)
f[u][i]=f[f[u][i-1]][i-1];
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(v==f[u][0])continue;
dep[v]=dep[u]+1,f[v][0]=u;
dfs(v);
}
}void Dfs(int u){
f1[u]=INF;f2[u]=siz[u]=0;
if(isq[u])siz[u]=1,f1[u]=0;
for(int i=Head[u];i;i=E[i].nxt)
Dfs(E[i].v);
for(int i=Head[u];i;i=E[i].nxt){
int v=E[i].v,w=dep[v]-dep[u];
ans1+=siz[v]*(k-siz[v])*w;
if(siz[u]){
ans2=min(ans2,f1[u]+w+f1[v]);
ans3=max(ans3,f2[u]+w+f2[v]);
}
siz[u]+=siz[v];
f1[u]=min(f1[u],w+f1[v]);
f2[u]=max(f2[u],w+f2[v]);
}
isq[u]=Head[u]=0;
}int lca(int u,int v){
if(dep[u]<dep[v])swap(u,v);
for(int i=20;i>=0;--i)
if(dep[f[u][i]]>=dep[v])
u=f[u][i];
if(u==v)return u;
for(int i=20;i>=0;--i)
if(f[u][i]!=f[v][i])
u=f[u][i],v=f[v][i];
return f[u][0];
}bool cmp(int u,int v){return dfn[u]<dfn[v];}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1,u,v;i<n;++i)
cin>>u>>v,add(u,v),add(v,u);
dep[1]=1,dfs(1);
cin>>m;
while(m--){
cin>>k;
for(int i=1,x;i<=k;++i)
cin>>x,q.push_back(x),isq[x]=1;
sort(q.begin(),q.end(),cmp);
for(int i=0;i<k-1;++i)
q.push_back(lca(q[i],q[i+1]));
q.push_back(1);
sort(q.begin(),q.end());
q.erase(unique(q.begin(),q.end()),q.end());
sort(q.begin(),q.end(),cmp);
for(int i=0;i<(int)q.size()-1;++i)
Add(lca(q[i],q[i+1]),q[i+1]);
ans1=0,ans2=INF,ans3=-INF;Dfs(q[0]);
cout<<ans1<<' '<<ans2<<' '<<ans3<<'\n';
Tot=0;q.clear();
}
return 0;
}
P6199 [EER1] 河童重工
见点分治部分。
点分治
【模板】点分治 1
给定一棵有 \(n\) 个点的树,多次询问树上距离为 \(k\) 的点对是否存在。
先考虑只求过某个点的路径是否存在。我们依次对这个点的儿子 dfs,得出一个桶,与之前的儿子的桶合并。由于点数的限制,这里我们可以不受值域的复杂度影响。于是我们可以 \(O(n)\) 统计这样一种情况的个数。
考虑我们对一个点这样做以后,我们以后所有的路径为了保证不重不漏,都不应经过这个点,于是这个点将树分成了若干块,每块内我们可以再次计算。
但这样最终还是 \(O(n^2)\) 的,我们可以进行一个优化——每次照一棵树的重心求答案,然后将树剖开。因为中心的每个儿子大小都小于等于这棵树的一半,每一层递归树大小的规模就会少一半自然有复杂度 \(O(n\log n)\),并且在随机数据下很难跑满。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,M=1e7+5;
int head[N],tot;
struct edge{int v,w,nxt;}e[N<<1];
inline void add(int u,int v,int w){
e[++tot]=(edge){v,w,head[u]},head[u]=tot;
}
int vis[N],dis[N];
int siz[N],maxn[N],rt;
int ans[N],ques[N];
int tmp[M],judge[M];
int q[M],cnt;
int n,m;
inline void find(int u,int fa){
siz[u]=1;
maxn[u]=0;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(v==fa||vis[v])continue;
find(v,u);
siz[u]+=siz[v];
maxn[u]=max(maxn[u],siz[v]);
}
maxn[u]=max(maxn[u],cnt-maxn[u]);
if(maxn[u]<maxn[rt])rt=u;
}
inline void diss(int u,int fa){
tmp[++tmp[0]]=dis[u];
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(vis[v]||v==fa)continue;
dis[v]=dis[u]+e[i].w;
diss(v,u);
}
}
inline void calc(int u){
int p=0;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v,w=e[i].w;
if(vis[v])continue;
tmp[0]=0;
dis[v]=w;
diss(v,u);
for(int k=tmp[0];k;--k)
for(int l=1;l<=m;++l)
if(ques[l]>=tmp[k])
ans[l]|=judge[ques[l]-tmp[k]];
for(int k=tmp[0];k;--k)
q[++p]=tmp[k],judge[tmp[k]]=1;
}
for(int i=p;i;--i)
judge[q[i]]=0;
}
inline void solve(int u){
vis[u]=judge[0]=1;calc(u);
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(vis[v])continue;
cnt=siz[v];
maxn[rt=0]=0x3f3f3f3f;
find(v,0);
solve(rt);
}
}
signed main(){
cin>>n>>m;
for(int i=1,u,v,w;i<n;++i)
cin>>u>>v>>w,add(u,v,w),add(v,u,w);
for(int i=1;i<=m;++i)
cin>>ques[i];
solve(1);
for(int i=1;i<=m;++i){
if(ans[i])cout<<"AYE\n";
else cout<<"NAY\n";
}
return 0;
}
P2634 [国家集训队] 聪聪可可
一模一样的套路,就是开桶统计。
P4149 [IOI2011] Race
给一棵树,每条边有权。求一条简单路径,权值和等于
\(k\),且边的数量最小。
相当于在模板题的基础上再维护一下边数个数再取最小就行。
P4178 Tree
给定一棵 \(n\) 个节点的树,每条边有边权,求出树上两点距离小于等于 \(k\) 的点对数量。
把模板题的桶换成树状数组统计就行。
P4183 [USACO18JAN] Cow at Large P
一个显然的贪心结论就是一个叶结点只会被一个农民封锁。假设 Bessie 从结点 \(rt\) 出发,农民封锁的结点为 \(u\),\(p_i\) 为 \(i\) 结点最近的叶结点,则应该有 \(dis_{rt,u}\ge dis_{u,p_u}\) 且 \(dis_{rt,fa_u}< dis_{fa_u,p_{fa_u}}\),后者可以写成 \(dis_{rt,fa_u}\le dis_{u,p_{fa_u}}\),于是我们可以 \(n^2\) 求出每个点的答案。
答案不好快速求的原因就是有一个 \(fa\) 的限制,考虑转化,使得将所有满足第一个条件的点,点权加起来答案是一样的。我们发现去除第二个限制,对答案有贡献的点是若干棵子树,我们希望一棵子树的权值为 \(1\)。
联想树上差分,将 \(u,v\) 权值各加 \(1\),\(lca_{u,v}\) 权值减 \(2\),这是一个很好的抵消方式。我们将每个点点权设为 \(2-deg_i\),可以发现,这样一个子树的权值和为 \(1\),读者可以自行理解。
我们转化成了对于所有点 \(rt\),求 \(\sum_{v,dis_{rt,v}\ge dis_{v,p_v}}2-deg_v\)。当然不能继续枚举 \(rt\),我们使用点分治,对所有过分治中心的满足 \(dis_{u,v}\ge dis_{v,p_v}\) 点对 \((u,v)\) 加贡献。
现在重新定义,假设我们分治中心为 \(rt\),\(dep_i\) 为 \(i\) 到 \(rt\) 的距离,于是如果有 \(dep_u\ge dep_{p_v}-dep_v\),则 \(v\) 对 \(u\) 有贡献。将所有点的 \(dep_{p_i}-dep_i\) 求出后排序,维护单调性添加答案即可。
#include<bits/stdc++.h>
#define pii pair<int,int>
#define fi first
#define se second
#define mk make_pair
using namespace std;
const int N=7e4+5,INF=0x3f3f3f3f;
int n,head[N],tot;
int deg[N],disp[N];
int siz[N],maxn[N],rt,cnt;
int vis[N],ans[N],gty;
pii a[N],b[N];
struct edge{int v,nxt;}e[N<<1];
void add(int u,int v){
e[++tot]=(edge){v,head[u]},head[u]=tot;
}void dfs1(int u,int fa){
disp[u]=INF;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(v==fa)continue;
dfs1(v,u);
if(disp[v]+1<disp[u])
disp[u]=disp[v]+1;
}if(deg[u]==1)disp[u]=0;
}void dfs2(int u,int fa){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(v==fa)continue;
if(disp[u]+1<disp[v])
disp[v]=disp[u]+1;
dfs2(v,u);
}
}void diss(int u,int fa,int dis){
a[++gty]=mk(dis,u);
b[gty]=mk(disp[u]-dis,2-deg[u]);
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(v==fa||vis[v])continue;
diss(v,u,dis+1);
}
}void calc(int u,int d,int typ){
diss(u,gty=0,d);
sort(a+1,a+gty+1);
sort(b+1,b+gty+1);
for(int i=1,j=0,s=0;i<=gty;++i){
while(j<gty&&b[j+1].fi<=a[i].fi)
s+=b[++j].se;
ans[a[i].se]+=s*typ;
}
}void find(int u,int fa){
maxn[u]=0,siz[u]=1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(vis[v]||v==fa)continue;
find(v,u),siz[u]+=siz[v];
maxn[u]=max(maxn[u],siz[v]);
}maxn[u]=max(maxn[u],cnt-siz[u]);
if(maxn[u]<maxn[rt])rt=u;
}void solve(int u){
vis[u]=1;calc(u,0,1);
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(vis[v])continue;
calc(v,1,-1);
cnt=siz[v],maxn[rt=0]=INF;
find(v,0),solve(rt);
}
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1,u,v;i<n;++i)
cin>>u>>v,add(u,v),add(v,u),
++deg[u],++deg[v];
dfs1(1,0),dfs2(1,0);
maxn[rt=0]=INF;
cnt=n,find(1,0);
solve(rt);
for(int i=1;i<=n;++i)
cout<<(deg[i]==1?1:ans[i])<<'\n';
return 0;
}
AT_cf17_final_j Tree MST
对于完全图生成树有一个结论就是如果我们总边集 \(S\) 从中取出一个 \(E\subseteq S\) 单独做生成树时,其中一些边落选,那么这些边在 \(S\) 做生成树时更不会被选上
于是我们可以将 \(S\) 分出若干个小集合,单独生成树,扔掉大部分边,只留一小部分有用的做生成树。
具体的,我们使用点分治枚举所有过分治中心 \(rt\) 的路径,将所有点按照 \(dis_{rt,i}+a_i\) 排序,那么这样一个子集的生成树就是将权值最小的那个点向其他所有点连边。
最终得到一个一棵大小为 \(O(n\log n)\) 的边集,直接 kruskal 就行了。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5,INF=1e17;
int n,a[N];
int ans;
int head[N],tot,Tot;
struct edge{int v,w,nxt;}e[N*2];
struct Edge{int u,v,w;}kru[N*20];
inline void add(int u,int v,int w){
e[++tot]=(edge){v,w,head[u]},head[u]=tot;
}
int fa[N];
int finde(int u){
return fa[u]==u?u:fa[u]=finde(fa[u]);
}
bool vis[N];
int siz[N],maxn[N],rt,cnt;
int dis[N],st[N];
inline bool cmp1(int x,int y){return dis[x]+a[x]<dis[y]+a[y];}
inline bool cmp2(Edge x,Edge y){return x.w<y.w;}
void find(int u,int fa){
siz[u]=1;maxn[u]=0;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(vis[v]||v==fa)continue;
find(v,u);
siz[u]+=siz[v];
maxn[u]=max(maxn[u],siz[v]);
}
maxn[u]=max(maxn[u],cnt-siz[u]);
if(maxn[u]<maxn[rt])rt=u;
}
void diss(int u,int fa){
st[++st[0]]=u;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(vis[v]||v==fa)continue;
dis[v]=dis[u]+e[i].w;
diss(v,u);
}
}
inline void calc(int u){
dis[u]=st[0]=0;diss(u,0);
sort(st+1,st+st[0]+1,cmp1);
for(int i=1;i<=st[0];++i){
kru[++Tot].u=st[1];
kru[Tot].v=st[i];
kru[Tot].w=a[st[1]]+a[st[i]]+dis[st[1]]+dis[st[i]];
}
}
void solve(int u){
calc(u);vis[u]=1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(vis[v])continue;
cnt=siz[v];
maxn[rt=0]=INF;
find(v,0);
solve(rt);
}
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;++i)
cin>>a[i];
for(int i=1,u,v,w;i<n;++i)
cin>>u>>v>>w,add(u,v,w),add(v,u,w);
maxn[rt=0]=cnt=n;
find(1,0);
solve(rt);
sort(kru+1,kru+Tot+1,cmp2);
for(int i=1;i<=n;++i)
fa[i]=i;
for(int i=1;i<=Tot;++i){
int u=finde(kru[i].u),v=finde(kru[i].v);
if(u!=v)fa[u]=v,ans+=kru[i].w;
}
cout<<ans;
return 0;
}
说个好玩的,笔者在打一场NOIP模拟赛T1时想到了这样的类似做法求最大生成树,虽然比较**,但是可以介绍一下做法。就是对于一个分治中心,求出与分治中心最远的点和次远的点,且不在同一子树,然后将所有的非最远子树内的点向最远的点连边,将最远的点子树内的点往次远的点连边,最终组成一个大集合,就可以求最大树生成树啦。
P6199 [EER1] 河童重工
比上一题简单多了。
考虑先在 \(T2\) 进行点分治,大体和上一题是一样的。但是这里需要考虑两棵树的限制。
对于 \(T2\) 的一个分治子树,我们建出子树中的点在 \(T1\) 上的虚树,连接 \(u,v\) 的代价我们可以看做 \(dep_u+dep_v+dis_{u,v}\),\(dep_i\) 为 \(T2\) 上的深度,\(dis_{x,y}\) 是 \(T1\) 上两点的距离。
考虑对于一个点分治时遇到的一个点 \(x\),在 \(T1\) 新建一个点 \(x_0\),连一条 \((x,x_0,dep_x)\) 的边,注意 \(x\) 是点分治遇到的,虚树后加的不算。我们求出虚树上每个 \(x\) 距离最近的新加点 \(p_x\) 以及距离 \(d_x\)。最终我们对于虚树上的一条边 \((x,y)\),将边 \((p_x,p_y,d_x+d_y+w_{u,v}))\) 加入 kruskal 候选集合。
#include<bits/stdc++.h>
#define int long long
#define pb push_back
using namespace std;
const int N=1e5+5,INF=1e17;
struct edge{int u,v,w;};
vector<edge>e1[N],e2[N],e3[N],kru;
vector<int> q;
int n,lg[N],fa[N],val[N];
int dep[N],dfn[N],st[N][19],idx;
int vis[N],siz[N],maxn[N],rt,tot;
int d1[N],d2[N],p1[N],p2[N];
bool cmp1(edge x,edge y){return x.w<y.w;}
bool cmp2(int x,int y){return dfn[x]<dfn[y];}
int get(int x,int y){return dfn[x]<dfn[y]?x:y;}
int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
int kruskal(){
for(int i=1;i<=n;++i)
fa[i]=i;
sort(kru.begin(),kru.end(),cmp1);
int res=0;
for(edge it:kru){
if(find(it.u)==find(it.v))continue;
res+=it.w,fa[find(it.u)]=find(it.v);
}return res;
}void dfs(int u,int fa){
st[dfn[u]=++idx][0]=fa;
for(edge it:e1[u])
if(it.v!=fa)
dep[it.v]=dep[u]+it.w,dfs(it.v,u);
}int lca(int u,int v){
if(u==v)return u;
if((u=dfn[u])>(v=dfn[v]))swap(u,v);
int d=lg[v-u++];
return get(st[u][d],st[v-(1<<d)+1][d]);
}void init1(){
dfs(1,0);
for(int j=1;j<=18;++j)
for(int i=1;i+(1<<j)-1<=n;++i)
st[i][j]=get(st[i][j-1],st[i+(1<<j-1)][j-1]);
}void find(int u,int fa){
siz[u]=1,maxn[u]=0;
for(edge it:e2[u]){
if(it.v==fa||vis[it.v])continue;
find(it.v,u),siz[u]+=siz[it.v];
maxn[u]=max(maxn[u],siz[it.v]);
}maxn[u]=max(maxn[u],tot-siz[u]);
if(maxn[u]<maxn[rt])rt=u;
}void diss(int u,int fa){
q.pb(u);
for(edge it:e2[u])
if(!vis[it.v]&&it.v!=fa)
val[it.v]=val[u]+it.w,diss(it.v,u);
}void upd(int u,int x,int y){
if(x<d1[u])d2[u]=d1[u],p2[u]=p1[u],d1[u]=x,p1[u]=y;
else if(x<d2[u])d2[u]=x,p2[u]=y;
}void dfs1(int u){
for(edge it:e3[u])
dfs1(it.v),upd(u,d1[it.v]+it.w,p1[it.v]);
}void dfs2(int u){
kru.pb((edge){u,p1[u],val[u]+d1[u]});
for(edge it:e3[u]){
if(p1[u]==p1[it.v])
upd(it.v,d2[u]+it.w,p2[u]);
else upd(it.v,d1[u]+it.w,p1[u]);
kru.pb((edge){p1[u],p1[it.v],d1[u]+d1[it.v]+it.w});
dfs2(it.v);
}d1[u]=d2[u]=val[u]=INF,p1[u]=p2[u]=0;
e3[u].clear();
}void calc(int u){
val[u]=0,diss(u,0);
sort(q.begin(),q.end(),cmp2);
int k=q.size();
for(int i=0;i<k;++i)
d1[q[i]]=val[p1[q[i]]=q[i]];
q.pb(1);
for(int i=0;i<k-1;++i)
q.pb(lca(q[i],q[i+1]));
sort(q.begin(),q.end());
q.erase(unique(q.begin(),q.end()),q.end());
sort(q.begin(),q.end(),cmp2);
for(int i=0;i<(int)q.size()-1;++i){
int lc=lca(q[i],q[i+1]);
e3[lc].pb((edge){lc,q[i+1],dep[q[i+1]]-dep[lc]});
}dfs1(1);dfs2(1);q.clear();
}void solve(int u){
calc(u);vis[u]=1;
for(auto it:e2[u]){
int v=it.v;if(vis[v])continue;
maxn[rt=0]=N;tot=siz[v];
find(v,0);solve(rt);
}
}signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;++i)
lg[i]=__lg(i),d1[i]=d2[i]=val[i]=INF;
for(int i=1,u,v,w;i<n;++i)
cin>>u>>v>>w,e1[u].pb((edge){u,v,w}),e1[v].pb((edge){v,u,w});
for(int i=1,u,v,w;i<n;++i)
cin>>u>>v>>w,e2[u].pb((edge){u,v,w}),e2[v].pb((edge){v,u,w});
init1();maxn[rt=0]=N;tot=n;
find(1,0);solve(rt);
cout<<kruskal()<<'\n';
return 0;
}
CF150E Freezing with Style
做中位数有一个方法就是二分答案,将 \(\ge mid\) 的边设为 \(1\),其余设为 \(-1\),判断是否存在 \(\ge0\) 的路径。
考虑点分治计算,我们对于一个 \(rt\) 向一个子树 dfs,设某个点深度为 \(x\),则我们要查询已有的深度在 \([L-x,R-x]\) 之间的最大值。滑动区间可以使用单调队列,但是我们每遍历一个子树,初始化队列会需要将很多点塞到队列中,复杂度仍然是不对的。
考虑一个优化,就是我们初始队列不需要将整个值域都加进去,只需要加到最长的路径长度,所以将遍历子树的顺序按照其 \(maxdep\) 递增遍历就行。复杂度是对的,因为 \(O(\sum_i maxdep_i)=O(n)\),而如果不优化复杂度最坏能达到 \(O(n\times maxdep)=O(n^2)\)。
由于还有个排序,所以最终复杂度 \(O(n\log^2n)\)。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,INF=0x3f3f3f3f;
inline int read(){
int x=0;char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return x;
}
inline void Max(int &u,int v){u=max(u,v);}
inline void Min(int &u,int v){u=min(u,v);}
int n,L,R,ans1,ans2;
int head[N],tot;
struct edge{int v,w,nxt;}e[N<<1];
inline void add(int u,int v,int w){
e[++tot]=(edge){v,w,head[u]},head[u]=tot;
}
bool vis[N];
int siz[N],maxn[N],cnt,rt,val;
void find(int u,int fa){
siz[u]=1;maxn[u]=0;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(v==fa||vis[v])continue;
find(v,u);
siz[u]+=siz[v];
maxn[u]=max(maxn[u],siz[v]);
}maxn[u]=max(maxn[u],cnt-siz[u]);
if(maxn[u]<maxn[rt])rt=u;
}
int q[N],l,r;
int son[N];
int f[N],df[N],g[N],dg[N];
int dep[N],dis[N],maxdep[N];
inline bool cmp(int x,int y){return maxdep[x]<maxdep[y];}
void diss(int u,int fa,int rt){
Max(maxdep[rt],dep[u]);
if(dis[u]>g[dep[u]])
g[dep[u]]=dis[u],dg[dep[u]]=u;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v,w=e[i].w;
if(v==fa||vis[v])continue;
dep[v]=dep[u]+1;
dis[v]=dis[u]+(w>=val?1:-1);
diss(v,u,rt);
}
}
bool calc(int u){
int num=0,Maxdep=0;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(vis[v])continue;
son[++num]=v;
dep[v]=1;dis[v]=(e[i].w>=val?1:-1);
diss(v,u,v);
Max(Maxdep,maxdep[v]);
}sort(son+1,son+num+1,cmp);
for(int i=0;i<=Maxdep;++i)
g[i]=f[i]=-INF,df[i]=dg[i]=0;
f[0]=0;df[0]=u;
for(int i=1;i<=num;++i){
int v=son[i],now=0;
diss(v,u,v);
l=1,r=0;
for(int j=min(R,Maxdep);j>=0;--j){
while(now<=maxdep[son[i-1]]&&now+j<=R){
while(l<=r&&f[q[r]]<f[now])--r;
q[++r]=now++;
}
while(l<=r&&q[l]+j<L)++l;
if(l<=r&&q[l]+j<=R&&f[q[l]]+g[j]>=0)
return (ans1=df[q[l]],ans2=dg[j],1);
}
for(int j=0;j<=maxdep[v];++j){
if(g[j]>f[j])
f[j]=g[j],df[j]=dg[j];
g[j]=-INF;dg[j]=0;
}
}return 0;
}
bool solve(int u){
if(calc(u))return 1;vis[u]=1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(vis[v])continue;
rt=0;cnt=siz[v];find(v,u);
if(solve(rt))return 1;
}return 0;
}
inline bool judge(){
for(int i=1;i<=n;++i)vis[i]=0;
ans1=ans2=0;
maxn[rt=0]=INF;cnt=n;
find(1,0);
return solve(rt);
}
signed main(){
n=read(),L=read(),R=read();
int l=INF,r=0;
for(int i=1,u,v,w;i<n;++i)
u=read(),v=read(),w=read(),Min(l,w),Max(r,w),add(u,v,w),add(v,u,w);
while(l<r){
val=(l+r+1)>>1;
if(judge())l=val;
else r=val-1;
}val=l;judge();
cout<<ans1<<' '<<ans2;
return 0;
}
P4292 [WC2010] 重建计划
将上一题的中位数换成平均数,其实做法一模一样,但是特别卡常,所以要预处理每次 find 的结果,直接去处理。
#include<bits/stdc++.h>
#define int long long
#define db double
#define pb push_back
using namespace std;
const int N=1e5+5,INF=0x3f3f3f3f;
int n,L,R,head[N],tot;
int vis[N];
int siz[N],maxn[N],cnt,rt,RT;
int dep[N],maxdep[N];
int q[N],l,r;
int son[N];
db dis[N],f[N],g[N];
vector<int> E[N];
struct edge{int v,nxt;db w;}e[N<<1];
void Max(int &x,int y){
if(y>x)x=y;
}void add(int u,int v,db w){
e[++tot]=(edge){v,head[u],w},head[u]=tot;
e[++tot]=(edge){u,head[v],w},head[v]=tot;
}void find(int u,int fa){
siz[u]=1;maxn[u]=0;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(v==fa||vis[v])continue;
find(v,u);siz[u]+=siz[v];
maxn[u]=max(maxn[u],siz[v]);
}maxn[u]=max(maxn[u],cnt-siz[u]);
if(maxn[u]<maxn[rt])rt=u;
}bool cmp(int x,int y){
return maxdep[x]<maxdep[y];
}void diss(int u,int fa,int rt,int V){
Max(maxdep[rt],dep[u]);
if(dis[u]>g[dep[u]])
g[dep[u]]=dis[u];
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(v==fa||vis[v]<V)continue;
dep[v]=dep[u]+1;
dis[v]=dis[u]+e[i].w;
diss(v,u,rt,V);
}
}bool calcium(int u){
int num=0,Maxdep=0;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(vis[v]<vis[u])continue;
son[++num]=v;
dep[v]=1;dis[v]=e[i].w;
diss(v,u,v,vis[u]);
Max(Maxdep,maxdep[v]);
}sort(son+1,son+num+1,cmp);
for(int i=0;i<=Maxdep;++i)
g[i]=f[i]=-INF;
f[0]=0;
for(int i=1;i<=num;++i){
int v=son[i],now=0;
diss(v,u,v,vis[u]);
l=1,r=0;
for(int j=min(R,Maxdep);j>=0;--j){
while(now<=maxdep[son[i-1]]&&now+j<=R){
while(l<=r&&f[q[r]]<f[now])--r;
q[++r]=now++;
}
while(l<=r&&q[l]+j<L)++l;
if(l<=r&&q[l]+j<=R&&f[q[l]]+g[j]>=0)
return 1;
}
for(int j=0;j<=maxdep[v];++j){
if(g[j]>f[j])
f[j]=g[j];
g[j]=-INF;
}
}return 0;
}void init(int u){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;if(vis[v])continue;
rt=0;cnt=siz[v];find(v,u);
vis[rt]=vis[u]+1;
E[u].pb(rt),init(rt);
}
}bool solve(int u){
if(calcium(u))return 1;
for(int v:E[u])
if(solve(v))return 1;
return 0;
}bool judge(db x){
for(int i=1;i<=tot;++i)
e[i].w-=x;
int res=solve(RT);
for(int i=1;i<=tot;++i)
e[i].w+=x;
return res;
}signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>L>>R;
for(int i=1,u,v,w;i<n;++i)
cin>>u>>v>>w,add(u,v,w);
maxn[rt=0]=INF;cnt=n;
find(1,0);
vis[RT=rt]=1,init(rt);
db l=-1e6,r=1e6;
while(r-l>1e-4)
if(judge((l+r)/2))l=(l+r)/2;
else r=(l+r)/2;
cout<<fixed<<setprecision(3)<<l<<'\n';
return 0;
}
长链剖分
我们将重链剖分改一下,将子树深度最深的作为“重儿子”,更换了一种剖分方式,考虑其性质。
- 任何节点达到 \(rt\) 的长链数不超过 \(O(\sqrt n)\)。
- 一个结点的 \(k\) 级祖先所在长链长度一定 \(\ge k\)。
P5903 【模板】树上 K 级祖先
很无用的一个东西,可以跳。
倍增做是 \(\log n\) 的,原因是要精确到 \(k\),前面很快,后面就慢下来了。所以我们使用长剖。具体的先用倍增跳到一个尽可能远的 \(2^h\) 的位置,此时我们只用向上跳不超过 \(\lfloor\frac k2\rfloor\) 的长度,必然小于当前节点所在链的长度。
从当前节点跳到链顶,将 \(k\) 减去对应长度。如果 \(k<0\),则向下在这条长链跳,反之向父亲所在的长链向上跳。由于长剖的性质,我们可以直接预处理出一个链顶向上和向下的信息。
#include<bits/stdc++.h>
#define N 500005
#define LL long long
using namespace std;
inline int read(){
int x=0;char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return x;
}
int n,m,u,v,cnt,fa[N][21],w[N],h[N];
int g[N],top[N],dep[N],id[N],U[N],D[N];
vector<int>edge[N];
void dfs1(int x){
for(int i=1;i<=19;++i)fa[x][i]=fa[fa[x][i-1]][i-1];
for(int i=0;i<edge[x].size();++i){
dep[edge[x][i]]=h[edge[x][i]]=dep[x]+1;
dfs1(edge[x][i]);
h[x]=max(h[x],h[edge[x][i]]);
if(h[edge[x][i]]>h[w[x]])w[x]=edge[x][i];
}
}
void dfs2(int x,int p){
id[x]=++cnt;
D[cnt]=x;
U[cnt]=p;
if(w[x]){top[w[x]]=top[x];dfs2(w[x],fa[p][0]);}
for(int i=0;i<edge[x].size();++i)
if(edge[x][i]!=w[x]){
top[edge[x][i]]=edge[x][i];
dfs2(edge[x][i],edge[x][i]);
}
}
int rt;
#define ui unsigned int
ui S;
inline ui get() {
S ^= S << 13;
S ^= S >> 17;
S ^= S << 5;
return S;
}
inline int ask(register int x,register int k){
if(!k)return x;
x=fa[x][g[k]];k-=(1<<g[k]);
k-=dep[x]-dep[top[x]];x=top[x];
if(k>=0) return U[id[x]+k];
return D[id[x]-k];
}
int main(){
n=read();m=read();
scanf("%u",&S);
g[0]=-1;
rt=1;
for(int i=1;i<=n;++i){
fa[i][0]=read();
if(!fa[i][0])rt=i;
else edge[fa[i][0]].push_back(i);
g[i]=g[i>>1]+1;
}
dep[rt]=1;dfs1(rt);
top[rt]=rt;dfs2(rt,rt);
LL ans=0;
int lans=0;
for(int i=1,x,k;i<=m;++i){
x=(get()^lans)%n+1,k=(get()^lans)%dep[x];
lans=ask(x,k);
ans^=(LL)i*lans;
}
cout<<ans;
return 0;
}
CF1009F Dominant Indices
长剖的真正作用——优化 DP。
很显然的,我们设 \(f_{u,i}\) 为节点 \(u\) 子树内距离为 \(i\) 的点有几个。我们有 \(f_{u,i}=\sum_{v\in son(u)} f_{v,i-1}\)。直接做是 \(O(n^2)\) 的,考虑使用长剖。对于一个节点 \(u\),先遍历其长儿子并将信息传上来,再遍历重儿子暴力合并。暴力也是有讲究的,我们只用枚举到 \(v\) 的所在链长,这由长链剖分的性质可得。
于是我们的复杂度就是所有剖链的长度和也就是 \(O(n)\)。在实现上,使用指针,让一条重链使用长度为其链长的 DP 数组。
本题还有较为明显的线段树合并做法。
#include<bits/stdc++.h>
#define int long long
#define pb push_back
using namespace std;
const int N=2e6+5,INF=1e17;
vector<int> e[N];
int n,ans[N],g[N],*f[N];
int dep[N],len[N],son[N],cnt;
void dfs1(int u,int fa){
for(int v:e[u]){
if(v==fa)continue;
dep[v]=dep[u]+1,dfs1(v,u);
if(len[v]>len[son[u]])
son[u]=v;
}len[u]=len[son[u]]+1;
}void dfs2(int u,int fa){
if(son[u]){
f[son[u]]=f[u]+1;
dfs2(son[u],u);
ans[u]=ans[son[u]]+1;
}for(int v:e[u]){
if(v==fa||v==son[u])continue;
f[v]=g+cnt;cnt+=len[v]+1;
dfs2(v,u);
for(int i=1;i<=len[v]+1;++i){
f[u][i]+=f[v][i-1];
if(f[u][i]>f[u][ans[u]]||(f[u][i]==f[u][ans[u]]&&i<ans[u]))
ans[u]=i;
}
}f[u][0]=1;
if(f[u][ans[u]]<=1)ans[u]=0;
}signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1,u,v;i<n;++i)
cin>>u>>v,e[u].pb(v),e[v].pb(u);
dfs1(1,0);f[1]=g;cnt=len[1]+1,dfs2(1,0);
for(int i=1;i<=n;++i)
cout<<ans[i]<<'\n';
return 0;
}
P5904 [POI2014]HOT-Hotels 加强版
满足要求的 \((x,y,z)\) 定满足三个点到其中两个点的 lca 距离都为 \(d\)。
首先定义一个 \(f\),与上一题的定义一样,但是这不能够计算答案。我们再定义一个 \(g_{u,i}\) 表示再来一条长度为 \(i\) 的链接到 \(u\) 上产生三元组的数量。注意答案会在 \(f,g\) 转移时计算。
\(g\) 不好直接从子树转移,考虑依次将每个子树与目前总树合并。一种是子树内本来就有的,所以 \(g_{u,i}\gets g_{v,i+1}\),一种是两棵树中的链拼起来的,所以 \(g_{u,i}\gets f_{u,i}\times f_{v,i-1}\)。注意先转移 \(g\) 再转移 \(f\)。而答案的计算就是 \(ans\gets f_{u,i-1}\times g_{v,i}+g_{u,i}\times f_{v,i-1}\)。
由于 \(g\) 数组的特殊位置偏移,请注意指针的放置。
#include<bits/stdc++.h>
#define int long long
#define pb push_back
using namespace std;
const int N=1e6+5,INF=1e17;
vector<int> e[N];
int n,ans,*f[N],*g[N];
int gty[N],*cnt=gty;
int len[N],son[N];
void dfs1(int u,int fa){
for(int v:e[u]){
if(v==fa)continue;
dfs1(v,u);
if(len[v]>len[son[u]])
son[u]=v;
}len[u]=len[son[u]]+1;
}void dfs2(int u,int fa){
if(son[u]){
f[son[u]]=f[u]+1;
g[son[u]]=g[u]-1;
dfs2(son[u],u);
}++f[u][0];ans+=g[u][0];
for(int v:e[u]){
if(v==fa||v==son[u])continue;
f[v]=cnt,cnt+=len[v]+2<<1;
g[v]=cnt,cnt+=len[v]+2;
dfs2(v,u);
for(int i=0;i<len[v];++i){
if(i)ans+=f[u][i-1]*g[v][i];
ans+=g[u][i+1]*f[v][i];
}for(int i=1;i<=len[v];++i){
g[u][i-1]+=g[v][i];
g[u][i]+=f[u][i]*f[v][i-1];
f[u][i]+=f[v][i-1];
}
}
}signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1,u,v;i<n;++i)
cin>>u>>v,e[u].pb(v),e[v].pb(u);
dfs1(1,0);
f[1]=cnt,cnt+=len[1]+2<<1;
g[1]=cnt,cnt+=len[1]+2;
dfs2(1,0);cout<<ans<<'\n';
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号