DP 砸题1
模拟赛——连续段的价值
定义字母 \(c\) 的连续段为:字符串 \(s\) 中的某个子串,子串的每个字符都为 \(c\)。
定义 \(f_i\) 表示第 \(i\) 种字母的所有连续段的最长长度。如果该字母没有出现,则 \(f_i\) 为 \(0\)。
蜗蜗有一个长度为 \(n\) 的字符串 \(s\),其中每个字符是前 \(k\) 个小写字母或?。他想用前 \(k\) 个小写字母替换 \(s\) 中所有?。替换后,蜗蜗想让 \(min_{i=1}^k f_i\) 尽可能大,求最大值。
\(1\le n\le 2\times 10^5, 1\le k\le 17\), \(s\) 仅包含前 \(k\) 个小写字母或者?。
答案显然具有单调性,所以外面二分答案 \(mid\)。
然后 \(f_{i,s}\) 表示前 \(i\) 个位置,已经满足要求字符集合为 \(s\) 的状态是否可行。预处理区间 \(p_{i,c}\) 为 \(i\) 位置向后第一个满足 \(c\) 连续段长度 $\ge mid $ 的位置。复杂度 \(O(2^kn\log n)\)。
然后考虑两维状态而 dp 值只有 0/1,所以不妨设 \(f_{s}\) 表示已经满足要求字符集合为 \(s\) 的状态最少需要多长的前缀。枚举 \(s\) 中未出现的数,使 \(f_{s\cup j}\gets p_{f_s,j}\)。复杂度 \((2^kk\log n)\)。
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,k;
char s[N];
int p[N][18],f[1<<18];
int q[N][18];
bool check(int len){
for(int i=len;i<=n;++i){
int s=-1,t=0;
for(int j=0;j<k;++j)
if(p[i][j]-p[i-len][j])
s=j,++t;
if(t==2)continue;
if(t==1)q[i-len+1][s]=i;
if(t==0){
for(int j=0;j<k;++j)
q[i-len+1][j]=i;
}
}for(int j=0;j<k;++j)
q[n+1][j]=0x3f3f3f3f;
for(int i=n;i>=1;--i){
for(int j=0;j<k;++j)
if(!q[i][j])
q[i][j]=q[i+1][j];
}memset(f,0x3f,sizeof(f));
f[0]=0;
for(int i=0;i<(1<<k)-1;++i){
if(f[i]>=n)continue;
for(int j=0;j<k;++j){
if((i>>j)&1)continue;
int v=q[f[i]+1][j];
f[i|(1<<j)]=min(f[i|(1<<j)],v);
}
}for(int i=n;i>=1;--i){
for(int j=0;j<k;++j)
q[i][j]=0;
}return f[(1<<k)-1]<=n;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>k>>s+1;
for(int i=1;i<=n;++i){
for(int j=0;j<k;++j)
p[i][j]=p[i-1][j];
if(s[i]!='?')++p[i][s[i]-'a'];
}int l=0,r=(n+k-1)/k,ans=0;
while(l<=r){
int mid=l+r>>1;
if(check(mid))ans=mid,l=mid+1;
else r=mid-1;
}cout<<ans<<'\n';
return 0;
}
模拟赛——平面点集划分
二维平面上有 \(n\) 个点,每个点有两个属性值,第 \(i\) 个点的坐标为 \((x_i,y_i)\) 和两个属性值 \(a_i\) 和 \(b_i\)。将这些点划分为两个集合 \(A\) 和 \(B\),满足以下条件:
- 每个点要么属于集合 \(A\),要么属于集合 \(B\);
- 不存在集合 \(A\) 中的点 \((x_i,y_i)\) 和集合 \(B\) 中的点 \((x_j,y_j)\) 满足 \(x_i\ge x_j\) 且 \(y_i≤y_j\)(即 \(A\) 中的点不能在 \(B\) 中点的右下方)。
定义划分的价值为 \((\sum_{i\in A}a_i)+(\sum_{j∈B}b_j)\)
,求价值的最大值。
\(1\le n\le 2\times 10^5,1\le x_i,y_i,a_i,b_i\le 10^9\),保证任意一对 \((x_i,y_i)\) 互不相同。
将点集整体旋转,转化成 \(A\) 中的点不能在 \(B\) 中点的左下方.
然后 A,B 点的分布一定形如下图。
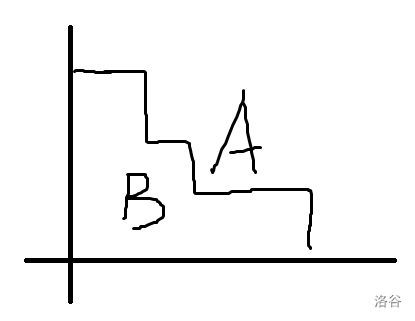
将所有点按 \(x\) 从小到大排,对于 \(x\) 相同的一起考虑。
\(f_{a,b}\) 表示前 \(x\le a\) 的点,放入 \(A\) 集合的点 \(y\) 最小值为 \(b\) 价值最大是多少。
考虑当前这一列将 $y<k $ 的点放到 \(B\) 里面,\(y\ge l\) 的丢进 \(A\)(意味着这一列 \(y\in [k,l-1]\) 没有点)。设其价值为 \(s\),则 \(f_{i,l}\gets f_{i-1,j}+s(j\ge l),f_{i,j}\gets f_{i-1,j}+s(k\le j<l)\)。
然后这玩意可以用线段树区间加,区间 \(\max\) 解决。
#include<bits/stdc++.h>
#define mid (l+r>>1)
#define ll long long
using namespace std;
const int N=4e5+5,M=1e9+1;
const ll F=1e15;
namespace SEG{
int ls[N*2],rs[N*2],rt,tot;
ll s[N*2],t[N*2];
void bd(int &p,int l,int r){
s[p=++tot]=-F;t[p]=0;if(l==r)return;
bd(ls[p],l,mid);bd(rs[p],mid+1,r);
}void pd(int p){
ll T=t[p];t[p]=0;
s[ls[p]]+=T;s[rs[p]]+=T;
t[ls[p]]+=T;t[rs[p]]+=T;
}void upd(int p,int l,int r,int x,ll y){
if(l==r){s[p]=max(s[p],y);return;}pd(p);
x<=mid?upd(ls[p],l,mid,x,y):upd(rs[p],mid+1,r,x,y);
s[p]=max(s[ls[p]],s[rs[p]]);
}void upd(int p,int l,int r,int L,int R,ll v){
if(L<=l&&r<=R){s[p]+=v;t[p]+=v;return;}pd(p);
if(L<=mid)upd(ls[p],l,mid,L,R,v);
if(mid<R)upd(rs[p],mid+1,r,L,R,v);
s[p]=max(s[ls[p]],s[rs[p]]);
}ll ask(int p,int l,int r,int L,int R){
if(L<=l&&r<=R)return s[p];pd(p);ll res=-F;
if(L<=mid)res=max(res,ask(ls[p],l,mid,L,R));
if(mid<R)res=max(res,ask(rs[p],mid+1,r,L,R));
return res;
}
}using namespace SEG;
int n,m,k,lsh[N*2];
vector<int> v[N*2];
int sy[N];ll sa[N],sb[N];
struct node{int x,y,a,b;}a[N];
bool cmp(int x,int y){
return a[x].y<a[y].y;
}void solve(){
cin>>n;
for(int i=1;i<=n;++i)
cin>>a[i].x>>a[i].y>>a[i].a>>a[i].b,
swap(a[i].x,a[i].y),a[i].y=M-a[i].y,
lsh[++m]=a[i].x,lsh[++m]=a[i].y;
sort(lsh+1,lsh+m+1);
m=unique(lsh+1,lsh+m+1)-lsh-1;
for(int i=1;i<=n;++i)
a[i].x=lower_bound(lsh+1,lsh+m+1,a[i].x)-lsh,
a[i].y=lower_bound(lsh+1,lsh+m+1,a[i].y)-lsh,
v[a[i].x].push_back(i);
bd(rt,1,m+1);upd(rt,1,m+1,m+1,0);
for(int i=1;i<=m;++i){
if(v[i].empty())continue;k=0;
sort(v[i].begin(),v[i].end(),cmp);
for(int o:v[i])
sy[++k]=a[o].y,
sa[k]=a[o].a,sb[k]=a[o].b;
for(int j=1;j<=k;++j)
sb[j]+=sb[j-1];
for(int j=k;j>=1;--j)
sa[j]+=sa[j+1];
sy[0]=0;sy[k+1]=m+1;
for(int j=0;j<=k;++j){
ll t=ask(rt,1,m+1,sy[j+1],m+1);
upd(rt,1,m+1,sy[j]+1,sy[j+1],sb[j]+sa[j+1]);
upd(rt,1,m+1,sy[j+1],t+sb[j]+sa[j+1]);
}
for(int j=0;j<=k+1;++j)
sy[j]=sa[j]=sb[j]=0;
v[i].clear();
}cout<<s[rt]<<'\n';
rt=tot=m=0;
}signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
int T;cin>>T;while(T--)solve();
return 0;
}
模拟赛——安全通道
给定一棵树,问有多少对 \(1\le i<j\le n\),使得添加边 \((i,j)\) 之后其最大独立集不变。
\(f_{i,0/1}\) 表示 \(i\) 的子树中,\(i\) 没选/选的最大独立集大小。然后初始做一遍 dp。
如果添加的边两端中有一个点本来就没选,那么这个方案一定可行。
如果两端都有,不妨以其中一个端点为根 \(rt\),做一遍 dp,判断 \(f_{rt,0}\) 是否等于答案。
那么我们可以拆贡献。如果一个点 \(u\) 为根时 \(f_{u,0}\) 等于答案,那么它与其他所有点连边时答案都不变。
设这样的点有 \(k\) 个,最终答案为 \(k(n-k)+\frac {k(k-1)}2\)。
对于求解 \(k\) 是一个简单换根。
#include<bits/stdc++.h>
#define eb emplace_back
using namespace std;
const int N=2.5e5+5;
int n,f[N][2],mx,k;
vector<int> e[N];
void dfs1(int u,int fa){
f[u][1]=1;
for(int v:e[u]){
if(v==fa)continue;
dfs1(v,u);
f[u][1]+=f[v][0];
f[u][0]+=max(f[v][1],f[v][0]);
}
}void dfs2(int u,int fa){
if(f[u][0]==mx)
++k;
for(int v:e[u]){
if(v==fa)continue;
int F1=f[u][1]-f[v][0];
int F0=f[u][0]-max(f[v][1],f[v][0]);
f[v][1]+=F0;
f[v][0]+=max(F0,F1);
dfs2(v,u);
}
}signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1,u,v;i<n;++i)
cin>>u>>v,e[u].eb(v),e[v].eb(u);
dfs1(1,0);
mx=max(f[1][0],f[1][1]);
dfs2(1,0);
cout<<1ll*k*(n-k)+1ll*k*(k-1)/2<<'\n';
return 0;
}
CF1874C Jellyfish and EVA
考虑倒着做 dp,\(f_i\) 表示
从 \(i\) 到 \(n\) 的成功概率最大值是多少。
考虑从 \(u\) 能到达 \(v_1,v_2,\cdots v_k\),根据一点贪心原理,我们肯定优先去成功概率高的地方。不妨令 \(g_{i,j}\) 表示有 \(i\) 个可能的走向,成功走向成功率第 \(j\) 大位置的概率。
g[i][j]
k=1 1
k=2 1/2 0
k=3 1/3 1/3 1/3
k=4 1/4
我们肯定优先选第一个数,设明日香选了 \(j\)。若 \(j=1\) 则成功,概率为 \(\frac 1n\),否则位置 \(j\) 将不可达,此时我们转化成了一个 \(n-2\) 规模的问题,只是新加一个 \(\frac 1n\) 的系数。
爆求 \(g\) 是 \(O(n^3)\) 的,随手推一下就发现 \(g_{i,j}\) 是 \(g_{i-2,j-1}\) 和 \(g_{i-2,j-2}\) 乘以一个系数相加,所以可以做到 \(O(n^2)\)。
倒着 dp 时,将可达点按 \(f\) 从大到小排序,按顺序乘上 \(g\) 即可。
#include<bits/stdc++.h>
#define pb push_back
#define db double
using namespace std;
const int N=5005;
int n,m,k;
db f[N],g[N][N],h[N];
vector<int> e[N];
void init(){
const int n=5000;
g[1][1]=1;g[2][1]=0.5;
for(int i=3;i<=n;++i){
g[i][1]=1.0/i;
for(int j=2;j<=i;++j)
g[i][j]=(g[i-2][j-1]*(i-j)+g[i-2][j-2]*(j-2))/i;
}
}void solve(){
cin>>n>>m;
for(int i=1,x,y;i<=m;++i)
cin>>x>>y,e[x].pb(y);
f[n]=1;
for(int i=n-1;i>=1;--i){
for(int v:e[i])
h[++k]=f[v];
sort(h+1,h+k+1,greater<db>());
for(int j=1;j<=k;++j)
f[i]+=h[j]*g[k][j];
k=0;
}cout<<fixed<<setprecision(10)<<f[1]<<'\n';
for(int i=1;i<=n;++i)
f[i]=0,e[i].clear();
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
init();
int T;cin>>T;while(T--)solve();
return 0;
}
CF780F Axel and Marston in Bitland
令 0 01 0110 01101001 等为正路径,1 10 1001 10010110 等为反路径。
这玩意一看就跟倍增有关系。令 \(f_{u,v,k,0/1}\) 为 \(u\) 到 \(v\) 长度为 \(2^k\) 的正/反路径是否存在。
\(f_{u,v,k,0/1}=\lor_{w=1}^n f_{u,w,k-1,0/1}\lor f_{w,v,k-1,1/0}\)。
这样玩复杂度是 \(O(n^3\log V)\) 的,可以用 bitset 优化一下就行。
计算答案时,再开一个 bitset 表示目前对于每个点是否可达。贪心考虑每一位,如果按位与之后非零,则可以走。
#include<bits/stdc++.h>
using namespace std;
const int N=503;
int n,m;long long ans;
bitset<N> bt[2][61][N],f,g;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1,u,v,w;i<=m;++i)
cin>>u>>v>>w,bt[w][0][u][v]=1;
for(int k=0;k<60;++k){
for(int u=1;u<=n;++u)
for(int w=1;w<=n;++w){
if(bt[0][k][u][w])
bt[0][k+1][u]|=bt[1][k][w];
if(bt[1][k][u][w])
bt[1][k+1][u]|=bt[0][k][w];
}
}g[1]=1;
for(int i=60,p=0;i>=0;--i){
f.reset();
for(int u=1;u<=n;++u)
if(g[u])f|=bt[p][i][u];
if(f.count())g=f,p^=1,ans|=(1ll<<i);
}cout<<(ans>1e18?-1:ans)<<'\n';
return 0;
}
CF1557D Ezzat and Grid
\(f_i\) 表示前 \(i\) 行,强制保留第 \(i\) 行,最少删多少行。枚举上一个保留的位置,只要两行有交集就可以转移,即 \(f_i\gets f_j+i-j\)。
既然只要有交集就可以转移,我们将 \(f_i+i\) 的值放到所有第 \(i\) 行所有黑的位置,和这里取 \(\min\)。
然后需要一棵区间取 \(\min\),区间求 \(\min\) 的线段树。
#include<bits/stdc++.h>
#define ll long long
#define pii pair<int,int>
#define eb emplace_back
#define mk make_pair
#define mid (l+r>>1)
#define fi first
#define se second
using namespace std;
const int N=3e5+5,M=2e6+5,F=1e9;
namespace SEG{
int ls[N*4],rs[N*4],rt,tot;
pii s[N*4],t[N*4];
void Min(pii &x,pii y){
if(y<x)x=y;
}void bd(int &p,int l,int r){
p=++tot;
t[p]=s[p]=mk(F,0);
if(l==r)return;
bd(ls[p],l,mid),bd(rs[p],mid+1,r);
}void pd(int p){
pii T=t[p];t[p]=mk(F,0);
Min(s[ls[p]],T);Min(s[rs[p]],T);
Min(t[ls[p]],T);Min(t[rs[p]],T);
}void upd(int p,int l,int r,int L,int R,pii v){
if(L<=l&&r<=R)return Min(s[p],v),Min(t[p],v);pd(p);
if(L<=mid)upd(ls[p],l,mid,L,R,v);
if(mid<R)upd(rs[p],mid+1,r,L,R,v);
s[p]=min(s[ls[p]],s[rs[p]]);
}pii ask(int p,int l,int r,int L,int R){
if(L<=l&&r<=R)return s[p];pd(p);pii res=mk(F,0);
if(L<=mid)Min(res,ask(ls[p],l,mid,L,R));
if(mid<R)Min(res,ask(rs[p],mid+1,r,L,R));
return res;
}
}using namespace SEG;
int n,m,ans=1e9;
int las[N],lsh[N*2],cnt;
vector<pii> v[N];
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1,x,l,r;i<=m;++i)
cin>>x>>l>>r,v[x].eb(mk(l,r)),
lsh[++cnt]=l,lsh[++cnt]=r;
sort(lsh+1,lsh+cnt+1);
cnt=unique(lsh+1,lsh+cnt+1)-lsh-1;
bd(rt,1,cnt);
for(int i=1;i<=n;++i){
int tmp=i-1;las[i]=0;
for(auto x:v[i]){
int l=lower_bound(lsh+1,lsh+cnt+1,x.fi)-lsh;
int r=lower_bound(lsh+1,lsh+cnt+1,x.se)-lsh;
pii tem=ask(rt,1,cnt,l,r);
if(tem.fi+i-1<tmp)
tmp=tem.fi+i-1,las[i]=tem.se;
}
if(tmp+n-i<ans)
ans=tmp+n-i,las[n+1]=i;
for(auto x:v[i]){
int l=lower_bound(lsh+1,lsh+cnt+1,x.fi)-lsh;
int r=lower_bound(lsh+1,lsh+cnt+1,x.se)-lsh;
upd(rt,1,cnt,l,r,mk(tmp-i,i));
}
}cout<<ans<<'\n';
for(int i=n+1;i;i=las[i])
for(int j=i-1;j>las[i];--j)
cout<<j<<' ';
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号