2025.8.22模拟赛
如果有原题的不再叙述题面。
T1
按照 \(t\) 逐位贪心匹配,每次要找到一个形如 \(i\) 位置之后第一个字符 \(c\) 出现的位置,这个直接将 \(s\) 倍长预处理即可。
赛时代码
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 3;
char s[N + N], t[N];
int n, m, ne[N + N][26], ans = 1;
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> s + 1 >> t + 1, n = strlen(s + 1), m = strlen(t + 1);
for (int i = 1; i <= n; ++i)
s[i + n] = s[i];
for (int j = 0; j < 26; ++j)
ne[n + n][j] = 1e9;
for (int i = n + n - 1; i >= 0; --i) {
for (int j = 0; j < 26; ++j)
ne[i][j] = ne[i + 1][j];
ne[i][s[i + 1] - 'a'] = i + 1;
}
for (int i = 0; i <= n; ++i)
for (int j = 0; j < 26; ++j)
if (ne[i][j] <= n + n)
ne[i][j] = (ne[i][j] - 1) % n + 1;
for (int i = 1, j = 0; i <= m; ++i) {
if (ne[j][t[i] - 'a'] > n)
return cout << -1 << '\n', 0;
if (ne[j][t[i] - 'a'] <= j)
++ans, j = ne[j][t[i] - 'a'];
else
j = ne[j][t[i] - 'a'];
}
cout << ans << '\n';
return 0;
}
T2
考虑删砝码的过程,若无论删 \([l,r]\) 哪边都不行,一定是 \([l,r-1]\) 和 \([l+1,r]\) 重心不在区间上。
故有解的充要条件为对于每一个 \(i\in [1,n]\),都存在一个长度为 \(i\) 的区间,其重心在答案区间上。必要性是显然的,充分性的话如果 \(i,i-1\) 两个长度都有合法的区间,\(i-1\) 的区间中必有长度为 \(i\) 的子区间,因为如果不是将其移动到 \(i\) 子区间内必然更居中于答案区间。
一种暴力的方法是将所有长度的区间抠出来,枚举重心最小值,记录重心最大值,然后就有 \(O(n^2\log n)\) 的做法。
赛时犯糖止步于这里了,只有 70pts。
赛时代码
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include <bits/stdc++.h>
#define dbz double
using namespace std;
const int N = 2e5 + 3;
int n;
dbz a[N], s[N], mx, ans = 1e18;
queue<dbz> q[N];
priority_queue<pair<dbz, int>> Q;
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 1; i <= n; ++i)
cin >> a[i], s[i] = s[i - 1] + a[i];
for (int len = 1; len <= n; ++len) {
for (int i = 1, j = len; j <= n; ++i, ++j)
q[len].push(1.0 * (s[j] - s[i - 1]) / len);
Q.push(make_pair(-q[len].front(), len));
mx = max(mx, q[len].front());
}
while (1) {
int u = Q.top().second;
ans = min(ans, mx + Q.top().first);
q[u].pop(), Q.pop();
if (q[u].empty())
break;
mx = max(mx, q[u].front());
Q.push(make_pair(-q[u].front(), u));
}
cout << fixed << setprecision(10) << ans << '\n';
return 0;
}
设 \([1,n]\) 区间的重心为 \(mid\),无论是猜测还是观察都能想到我们会选重心更接近 \(mid\) 的区间。而这里的接近是 \(\le mid\) 中最大的以及 \(\ge mid\) 中最小的。
证明大概是这样,如图红色为重心,假设我们向右选了第三条远离重心的我们如过回头向左,那么白白使右端点 \(\max\) 增加,如果继续向右那就答案左端点不变,右端点还在增加。不如直接选第四条重心靠近 \(mid\) 的区间。
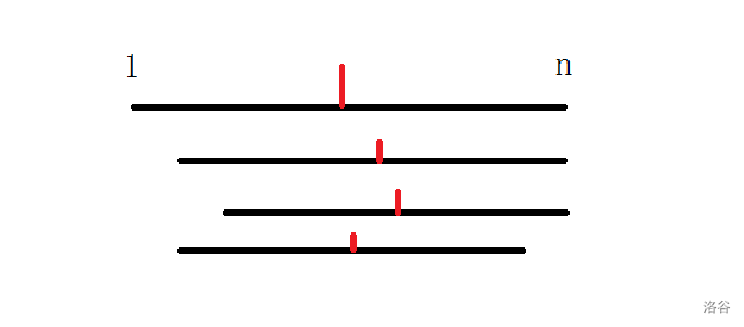
这样有用的区间被控在了 \(O(n)\) 范围内。复杂度 \(O(n\log n)\)。
赛后 100pts 代码
#include <bits/stdc++.h>
#define dbz double
#define pii pair<int, int>
using namespace std;
const int N = 2e5 + 3;
int n;
dbz a[N], s[N], mx, ans = 1e18;
int L[N], R[N];
queue<dbz> q[N];
priority_queue<pair<dbz, int>> Q;
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 1; i <= n; ++i)
cin >> a[i], s[i] = s[i - 1] + a[i];
dbz mid = 1.0 * s[n] / n;
L[n] = 1, R[n] = n;
q[n].push(mid);
Q.push(make_pair(-mid, n));
mx = max(mx, mid);
for (int i = n - 1; i >= 1; --i) {
R[i] = n;
for (int l = L[i + 1], r = l + i - 1; r <= R[i + 1]; ++l, ++r) {
q[i].push(1.0 * (s[r] - s[l - 1]) / i);
if (1.0 * (s[r] - s[l - 1]) / i <= mid)
L[i] = max(L[i], l);
else
R[i] = min(R[i], r);
}
Q.push(make_pair(-q[i].front(), i));
mx = max(mx, q[i].front());
}
while (1) {
int u = Q.top().second;
ans = min(ans, mx + Q.top().first);
q[u].pop(), Q.pop();
if (q[u].empty())
break;
mx = max(mx, q[u].front());
Q.push(make_pair(-q[u].front(), u));
}
cout << fixed << setprecision(10) << ans << '\n';
return 0;
}
T3
注:赛时将次数限制加强为 \(6300\),并将部分分改为关于次数的更严格的函数。
考虑从大到小枚举 \(i\),每次尝试将 \(i\) 归位,设当前 \(a_p=i\),选择 \((p,i)\) 这个操作可以将 \(p\) 走到 \(p\) 和 \(i\) 的距离除以 \(2\),故操作次数是 \(O(n\log n)\) 级别。据说可以先随机打乱以获得更高分数,但赛时我是只有 49pts。
赛时49pts代码
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include <bits/stdc++.h>
#define dbz double
using namespace std;
const int N=3003;
int n,a[N],b[N];
vector<pair<int,int>>ans;
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin>>n;
for(int i=1;i<=n;++i)
cin>>a[i];
for(int i=n;i>=1;--i){
int p=0;
for(int j=1;j<=i;++j)
if(a[j]==i)
p=j;
while(p<i){
ans.push_back(make_pair(p,i));
int l=p-1;
for(int j=p;j<=i;++j)
if((j-p)&1)
b[++l]=a[j];
for(int j=p;j<=i;++j)
if(!((j-p)&1))
b[++l]=a[j];
for(int j=p;j<=i;++j)
if((a[j]=b[j])==i)
p=j;
}
}
cout<<ans.size()<<'\n';
for(auto x:ans)
cout<<x.first<<' '<<x.second<<'\n';
return 0;
}
然后会发现考虑把排列取个逆,然后把操作也取个逆。每次可以将位置 \(p\) 的数移动到 \(2p\),并且当 \(2p\ge i\) 时直接调用 \((2p-i+1,i)\) 将 \(p\) 移动到 \(i\)。
引用题解:
假设当前的数要挪到 \(v\),若现在的位置 \(u\) 满足 \(u\ge 2^k\),则至多需要进行 \(\lfloor\log v\rfloor-k\) 次操作,随机化之后还原一个位置的期望步数为 \(O(1)\),从表现上来看,随机化之后有大约两倍的常数。
迷之操作,总之这是对的就行。
赛后 100pts 代码
#pragma GCC optimize(2)
#include <bits/stdc++.h>
using namespace std;
const int N = 3003;
int n, a[N], b[N];
vector<pair<int, int>> ans;
mt19937 rd(time(0));
void solve(int l, int r) {
ans.emplace_back(make_pair(l, r));
int k = l;
for (int i = l; i <= r; ++i)
b[i] = a[i];
for (int i = l + 1; i <= r; i += 2)
a[i] = b[k++];
for (int i = l; i <= r; i += 2)
a[i] = b[k++];
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 1, x; i <= n; ++i)
cin >> x, a[x] = i;
for (int i = 1, x, y; i <= 100; ++i)
x = rd() % n + 1, y = rd() % n + 1, solve(min(x, y), max(x, y));
for (int i = n; i >= 1; --i) {
int p = 0;
for (int j = 1; j <= i; ++j)
if (a[j] == i)
p = j;
while (p * 2 <= i)
solve(1, p *= 2);
if (p != i)
solve(p * 2 - i + 1, i);
}
reverse(ans.begin(), ans.end());
cout << ans.size() << '\n';
for (auto x : ans)
cout << x.first << ' ' << x.second << '\n';
return 0;
}
T4
赛时乱搞获得 16pts。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号