一些常用的数据结构维护手法

这篇会理论上讲一讲常用的数据结构维护手法。

我是嘴巴选手我自豪！

①cdq分治

现在我们有一些修改，有一些询问，修改之间独立。

我们考虑分治，对于左右两半分别分治，然后对于左边的修改计算对右边询问的贡献。

本身的复杂度是O(nlogn)。

②整体二分

现在我们有一些修改，有一些询问。

我们需要求出，在最少多少组修改之后满足题目条件。（或者可以转化成这样）

对于单组询问，我会二分！对于多组询问，真不巧，二分超时了...

我们考虑整体二分。整体二分的框架大概是这样：

def 整体二分(el,er,ql,qr):
    if el==er:
        ql到qr的答案都是el
        return 
    em=(el+er)/2
    模拟el...em的操作
    看一下ql...qr哪些满足了
    满足的放到ql...qm，不满足的放到qm+1...qr
    整体二分(em+1,er,qm+1,qr)
    撤销el...em的操作
    整体二分(el,em,ql,qm)

本身的复杂度是O(nlogn)的。

升级版（upd 2017.7.19）

有n条边，每条边有一个边权，对于每个i，你要对前i条边回答，加上边权<=几的边会没有奇数大小的联通块。

http://codeforces.com/contest/603/submission/14601511

def go(l,r,al,ar):
  #表示现在考虑操作[l,r]，答案边权在[al,ar]
  #编号<l，边权<al的边已经加好了
  mid=(l+r)/2
  记录一个状态ver
  for i in [l,mid]:
    如果i操作的边边权比al小就加边
  nmid=-1
  for i in [al,ar]:
    如果边权为i的边，操作编号为[l,mid]就加边
    如果没有奇数联通块了:
      nmid=i
      break
  回到状态ver
  if nmid==-1:
    [l,mid]答案为-1
    for i in [l,mid]:
      如果i操作的边边权比al小就加边
    go(mid+1,r,al,ar)
    回到状态ver
    return
  ans[mid]=nmid
  for i in [al,nmid-1]:
    如果边权为i的边，操作编号在[1,l-1]就加边
  go(l,mid-1,nmid,ar)
  回到状态ver
  for i in [l,mid]:
    如果i操作的边边权比al小就加边
  go(mid+1,r,al,nmid)
  回到状态ver

③时间倒流

现在我们有一些修改（例如删除边啥的），有一些询问。

修改反着做比正着做容易。

既然可以离线，干脆把修改倒过来做。

④根号重构

现在我们有一些修改，有一些询问，修改之间独立。

对于一堆修改计算对一堆询问的贡献复杂度比较高（例如和询问修改个数无关，而和其它东西有关），而单个修改对单个询问贡献复杂度很低。

同时我们可以用相对比较低的复杂度把一坨修改预处理一波，计算预处理之后的东西对单个询问贡献复杂度很低。

我们可以每根号个修改预处理一次，然后询问就枚举还没预处理的修改以及预处理好的算贡献就可以了。

本身的复杂度是O(n√n)。

⑤莫队

A.

现在我们没有修改，只有一大堆询问。

询问十分复杂，但是如果知道了[l,r]的答案，可以很快得到[l,r-1]和[l,r+1]和[l-1,r]和[l+1,r]的答案。

考虑把l分成根号块，把所有询问排序，按l所在的块编号为第一关键字，r为第二关键字排序，暴力拓展当前的区间。

本身的复杂度是O(n√n)。

B.（upd 2017.03.19）

现在我们没有修改，只有一大堆询问。

询问十分复杂，但是如果知道了[l,r]的答案，可以很快得到[l,r+1]和[l-1,r]的答案。

设p=sqrt(n)，那么对于长度<=2p的询问先暴力做。

对于长度>2p的，考虑把左端点按p间距分块，每次考虑左端点在同一块中的所有询问。

对于左端点在一块的询问，假装块范围为[l,r]，把这坨询问按右端点排序，假设某个询问为[p,q]，那么首先考虑[r+1,q]，因为q是递增的，所以大概可以拿个指针扫一遍，然后再插入[p,r]，插入完再撤销。（既然能插入显然也能撤销，大不了把所有修改过的内存地址记下来）

本身的复杂度还是O(n√n)。

⑥线段树分治

现在我们有一些区间修改，有一些单点询问，询问在所有修改之后。

A.

比较容易支持对当前状态进行修改，并撤销这次修改（如果不再进行其它修改）。

考虑对于区间建出线段树结构（只要结构），然后对于每个修改下放到log个区间，然后我们在线段树上分治，进这个点的时候进行这个点所有修改，出这个点的时候撤销这些修改，对于叶节点记录一下答案。

复杂度是O(nlogn*(修改/撤销)+n*询问)。

B.（upd 2016.12.26）

比较容易支持处理出一个区间的信息，询问信息可以合并。

还是对于区间建出线段树结构（只要结构），对于每个修改下放到log个区间，对于每个线段树节点预处理信息，单点询问时把它到线段树根节点上的链每个信息都查询一遍，合并在一起。

实际写的时候可以把询问先全部扔到链上的每个节点上，不用真的实时查询。

复杂度是O(nlogn*修改+nlogn*询问)。

一般来说B比较优秀，除非询问的东西实在比较特殊，询问大概慢一个log这样，而且还要兹磁撤销（我猜并没有这种题目？）

⑦二进制分组

现在我们有一些修改，有一些询问，修改之间独立。强制在线。

我们可以以一个与修改个数有关的时间预处理出一些修改的信息，对于一个询问可以快速地在预处理后的一些修改中获取信息。

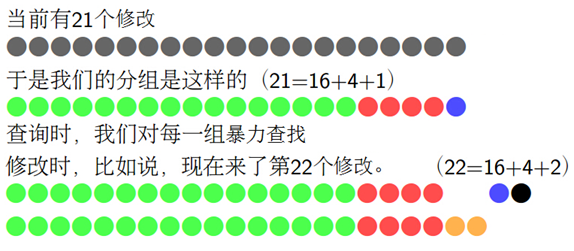
我们可以采用二进制分组的思想，感觉这种做法只能看图了...

（jiry：2048）

本身的复杂度是O(nlogn)。

⑧分治（upd 2017.03.22）

现在有一些询问，询问静态区间中一段的某些信息。询问支持离线，信息容易保存，用单点更新信息比信息合并快一个log。

考虑对于序列分治，每次把序列切成两段，考虑跨两段的询问，只要断点前后做一次前后缀和，对于询问合并一下一个后缀和一个前缀就好了。

假设信息合并是O(log)的，更新单点是O(1)的，那么复杂度就是O(nlogn)的。