数论学习_欧拉函数

       在数论，对正整数n，欧拉函数是小于n的正整数中与n互质的数的数目（φ(1)=1）。此函数以其首名研究者欧拉命名(Euler'so totient function)，它又称为Euler's totient function、φ函数、欧拉商数等。 例如φ(8)=4，因为1,3,5,7均和8互质。 从欧拉函数引伸出来在环论方面的事实和拉格朗日定理构成了欧拉定理的证明。    

        求解小于n且与n互素的整数个数。给出正整数n的唯一分解式: n=p1^a1p2^a2p3^a3......pk^ak,求1,2,3......n中与n互素的数的个数，不难想到用容斥定理求解，让n减去与n不互素的数，也就是pi的倍数。先减去不是pi的倍数得数，在加上是pipj倍数得数......这些很好计算就是n/pi,n/pipj。 n-n/p1-n/p2....-n/pk+n/p1p2+n/p1p3......换个思路想就是对于每个因子pi，要么贡献是1要么贡献是-1/pi,得 这就是著名的欧拉函数。

      下面讨论如何求解单个整数的欧拉函数值，显然可以找到这个数所有的质因子然后再依次计算，需要用到试除法依次判断sqrt(N)内所有的素数是否是N的因子。

这需要生成质数表。但其实并不用那么麻烦，只需要每次找到一个素因子之后把他除干净即可，可以保证找到的因子都是素数。

int euler_phi(int n)
{
    int m = sqrt(n + 0.5);
    int ans = n;
    for (int i = 2;i <= m;++i)
    {
        if (n%i == 0) {
            ans = ans / i*(i - 1);
            while (n%i == 0)n /= i;
        }
    }
    if (n > 1)ans = ans/n * (n - 1);
    return ans;
}

   上面的式子应该很容易看懂，最后一步是防止n是一个质数。

至于为什么循环到根号N，是因为对于任意的合数P至少有一个不大于sqrt(N)的素因子，至多有一个不小于sqrt(N)的素因子。所以最后pd下N是否除尽了。

　　　　

    如果要求多个数的欧拉函数的话，这样会显得很耗时，不妨使用打表法。

int phi[maxn];
void init(int N)
{
    for (int i = 2;i <= N;++i) phi[i] = 0;
    phi[1] = 1;
    for (int i = 2;i <= N;++i)
    {
        if (!phi[i]) {
            for (int j = i;j <= N;j += i) {
                if (!phi[j]) phi[j] = j;
                phi[j] = phi[j] / i*(i - 1);
            }
        }
    }
}

 

 

　　欧拉函数也可以利用类似于素数筛的欧拉筛法线性推倒出来，我们知道欧拉筛法保证了每个数都被最小的质因子筛除一次。又有以下定理 :

当p为素数时  phi(p)=p-1

当  i%prime[j]!=0 时，因为prime[j]是素数所以i和prime[j]互质 ，phi[i*prime[j]]=phi[i]*（prime[j]-1).

当 i%prime[j]==0时  phi[i*prime[j]]=prime[j]*phi[i];  这是因为一旦i%p==0,说明i的因子包含p，如果gcd(x,i)==1 --> gcd(x,i*p)==1,

又 gcd(n,m)==gcd(n+k*m,m) ,所以gcd(x,i)==1-->gcd(x+k*i,i)==1 --> gcd(c+k*i,i*p)==1，计算出i以内的互质数后放大到后面的区间即可，

所以答案就是 p*phi(i) ,将[1,i*p]分成了[1,i],[i+1,2*i]......[(p-1)*i+1,p*i]。

　　

void init(){
    f[1]=1;
    is[0]=is[1]=1;
    for(int i=2;i<=maxn;++i){
        if(!is[i]) prime.push_back(i),f[i]=i-1;
        for(int j=0;j<prime.size()&&1LL*i*prime[j]<=maxn;++j){
            is[i*prime[j]]=1;
            if(i%prime[j]==0){
                f[i*prime[j]]=f[i]*prime[j];
                break;
            }
            else{
                f[i*prime[j]]=f[i]*(prime[j]-1);
            }
        }
    }
}

 

欧拉定理:

    在数论中，欧拉定理,（也称费马-欧拉定理）是一个关于同余的性质。欧拉定理表明，若n,a为正整数，且n,a互质，则:  a^φ(n)≡1(mod n)

费马小定理:

a是不能被质数p整除的正整数，则有a^(p-1) ≡ 1 (mod p)

证明这个定理非常简单，由于p是质数，所以有φ(p) = p-1，代入欧拉定理即可证明。推论：对于任意正整数a，有a^p ≡ a (mod p)，因为a能被p整除时结论显然成立。

 

 

 欧拉函数的一些性质:

• 如果n是质数，则phi(n)=n-1
• 若p为质数，则phi(p^k)=p^k-p^k-1=(p-1)p^k-1
• 若m,n互质，则phi(mn)=phi(n)*phi(m)
• 若n为奇数，phi(2n)=phi(2)*phi(n)=phi(n)
• 对于所有的n>2,都有phi(n)%2==0； 可以这么考虑，phi(n)=phi(p1^a1p2^a2p3^a3*...*pk^ak)=∏phi(pi^ai), 由上面的定理2可知，无论p是奇数或是偶数，phi(p^a)都是偶数(奇-奇=偶，偶 - 偶=偶)。
• 若p为质数，i%p!=0 -> 则phi(i*p)=(p-1)*phi(i)                                                                                                                                                                  i%p==0->则phi(i*p)=p*phi(i)           //对于这个式子可以这么想，设i=p^kp1^a1p2^a2*...*pn^an,                                                    则phi(i)=(p-1)*p^k-1*phi(p1^a1)*...*phi(pn^an), phi(i*p)=(p-1)*p^k*phi(p1^a1)*...*phi(pn^an),显然phi(i*p)=p*phi(i)。

 

<欧拉定理>   a^phi(n) ≡ 1 (mod n)    //an互质

可以推出广义欧拉降幂公式:

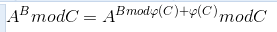
对于推导过程，若ac互质 ->  a^b % c = (a^phi(c)%c*a^phi(c)%c*...*a^k%c)%c = a^k%c =a^b%phi(c)%c