c++邻接表表示法创建无向图
--- --- # 6. 图 ## 6.1 图的定义和术语   >  > > > - **<vi,vj>**是弧,表示由**vi指向vj**,是一个**有向的弧**,称作**vi邻接到vj,vj邻接于vi**         ## 6.2 案例引入 案例一:六度空间理论  ## 6.3 图的类型定义    ## 6.4 图的存储结构  ### 6.4.1 邻接矩阵 #### 6.4.1.1 无向图的邻接矩阵   #### 6.4.1.2 有向图的邻接矩阵  #### 6.4.1.3 网的邻接矩阵  #### 6.4.1.4 邻接矩阵的存储表示和代码 **邻接矩阵的存储表示 :** 用两个数组分别存储**顶点表**和**邻接矩阵** ***图的定义*** ```c++ struct AMGraph { //图的顶点向量 char Vexs[MAXSIZE]; //图的邻接矩阵 int Arcs[MAXSIZE]; //图的总顶点数和总边数 int vexnum, arcnum; }; ``` ***创建无向网*** ```c++ void CreatUDN(AMGraph &G) { //第一步:输入无向图的顶点数目 cout << "input num" << endl; cin >> G.arcnum >> G.arcnum; //输入总顶点数和总边数 //第二步:输入结点的名称,保存在一维数组中 cout << "input vexs" << endl; for (int i = 0; i < G.vexnum; ++i) { cin >> G.vexs[i]; } //第三步:将邻接矩阵的元素值置为无穷大 for (int i = 0; i < G.arcnum; ++i) { for (int j = 0; j < G.arcnum; ++j) { G.arcs[i][j] = INT32_MAX; } } //第四步:输入顶点相互关系以及权重 for (int k = 0; k < G.arcnum;++k) { int i, j, weight; char a, b; cin >> a >> b >> weight; //由输入的顶点a和b查找到对应的下标i,j i = LocateVex(G,a) j = LocateVex(G,b) G.arcs[i][j] = G.arcs[j][i] = weight; } } ``` ***邻接矩阵的LocateVex函数*** ~~~cpp int LocateVex(AMGraph &G, const char &e) { for (int i = 0; i < G.vexnum;++i) { if(G.vexs[i]==e) return i; } return -1; } ~~~       #### 6.4.1.5 邻接矩阵的优缺点   ### 6.4.2 邻接表 #### 6.4.2.1 邻接表表示法(链式)  #### 6.4.2.2无向图的邻接表  #### 6.4.2.3 有向图的邻接表   #### 6.4.2.4 邻接表的存储表示和代码     ***邻接表定义代码*** ~~~cpp //顶点的结点定义 (表头) typedef struct VNode { //数据域,存放顶点信息 VecTexType data; //指针域,指向第一条依附该顶点的边的指针 / ArcNode *p / p->adjvex 即边指向顶点的位置编号 ArcNode *firstarc; } AdjList[MVNum]; //AdjList表示邻接表类型 //弧(边)的结点定义 struct ArcNode { int adjvex; //该边指向顶点的的位置编号 int weight; //保存边的权重 ArcNode *nextarc; //指向下一个边的指针 ArcNode //形成嵌套,不断形成指向下一个弧(边)的指针 }; //图定义 struct ALGraph { //定义一个数组,保存图的顶点 Maxsize = vexnum 顶点个数 VNode vexs[MAXSIZE]; // AdjList vertices // VNode结构体(第一段代码) //定义两个变量,保存当前图的顶点个数以及边的条数 int vexnum, arcnum; }; ~~~    ***创建无向图算法***  ~~~cpp void CreatUDG(ALGraph &G) { //输入图的顶点个数以及边的条数 cout << "info" << endl; cin >> G.vexnum >> G.arcnum; //给顶点向量赋值 for (int i = 0; i < G.vexnum; ++i) { cin >> G.vexs[i].data; G.vexs[i].firstarc = NULL; } //输入各边构建连接表 / 输入一条边依附的两个顶点 for (int j = 0; j < G.arcnum; ++j) { cout << "input info about arc" << endl; char a, b; //int w; cin >> a >> b; int i = LocateVex(G, a); //定位a结点的编号 int j = LocateVex(G, b);
// 出度边的构建 ArcNode *p1 = new ArcNode;//生成一个新的边节点*p1 p1->adjvex = j; //邻接点序号为j //p1->weight = w1; //权重1 p1->nextarc = G.vexs[i].firstarc; // 当前G.vexs[i].firstarc为NULL G.vexs[i].firstarc = p1; //将新节点*p1插入顶点vi的边表头部 (头插法) // 入度边的构建 ArcNode *p2 = new ArcNode; p2->adjvex = i; //p2->weight = w2; //权重2 p2->nextarc = G.vexs[j].firstarc; G.vexs[j].firstarc = p2; } }
由于是无向表,因此可以需要构建入度和出度表。有向表就只需要构建一个。。
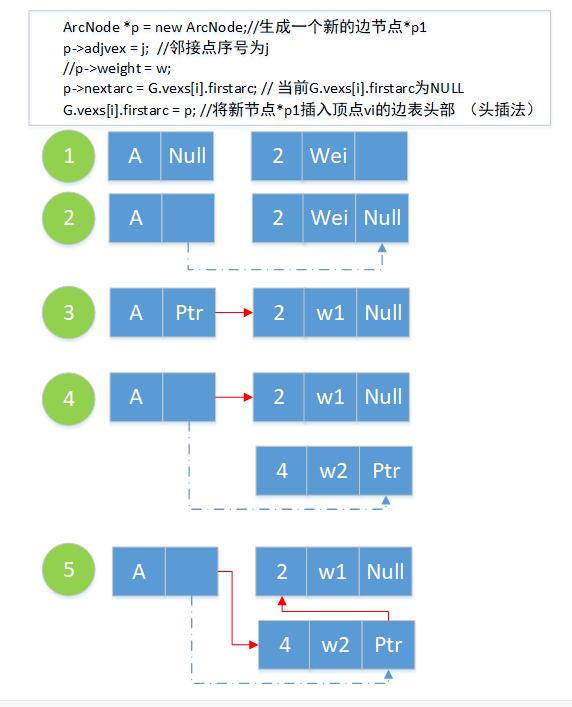
为什么说是头插法?特地画了个图




 浙公网安备 33010602011771号
浙公网安备 33010602011771号