数据结构(三)
数据结构(三)
哈希表
哈希表是一种映射,一般是将大范围数据映射到小范围内(便于存储方式便于查找并且节省了空间)
例如将1e9范围的数据映射到1e5范围内
即 [ 数值 ] mod [ 范围 ] 即可
范围取质数可使映射冲突的数最少
映射:不同于离散化的映射
哈希表的映射是一种无条件映射(会产生数据重合的冲突)
离散化映射则要求一个单调区间
开放寻址法和拉链法是哈希表的两种处理映射冲突方式
//找到大于1e5的第一个质数(10003)
bool b= true;
for(int i=1e5;;i++){
for(int j=2;j*j<=i;j++){
if(i%j==0)
b=false;
break;
}
if(b)cout<< i,break;
}

拉链法处理——遇到重复映射数值使其同时挂载在一个节点下
基本操作:
查找;插入;删除(标记该元素的boolean变量为false)
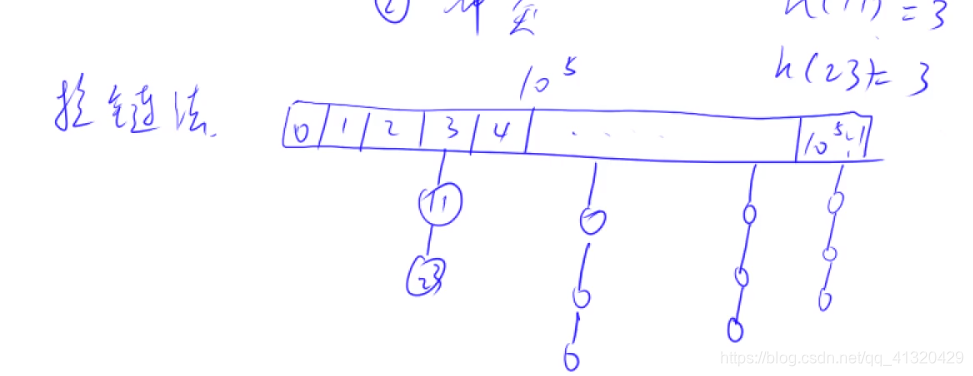
例题1 模拟散列表
拉链法实现哈希表

具体实现
即用数组链表的方式存取映射
需要数组h[n]下标对应映射,内容初始化为-1(作为头结点)
链表e[n],ne[n]存取数据
#include <iostream>
#include <cstring>
using namespace std;
const int N=100003;
int h[N],e[N],ne[N],idx; // h[N]链表头结点,相当于N个点组成一个链表头数组,存储下指向的下一个点,初始化指向-1,e[n]为数据域,ne[n]是指针域
int n;
void insert(int x){
int k=(x%N+N)%N; //求出x应该归于第k个链表,x有可能为负数,将其转化为正数
e[idx]=x; //初始化一个节点为x
ne[idx]=h[k];
h[k]=idx++;
}
int find(int x){
int k=(x%N+N)%N;
for(int i=h[k];i!=-1;i=ne[i]){
if(e[i]==x)
return true;
}
return false;
}
int main(){
cin>>n;
memset(h,-1,sizeof h); //将h[n]中全部的点初始化为头结点,值为-1
while(n--){
char op[2];
int x;
scanf("%s%d",op,&x);
if(op[0]=='I')insert(x);
else {
int flag=find(x);
if(flag)cout<<"Yes"<<endl;
else cout<< "No"<<endl;
}
}
return 0;
}
开放寻址法实现哈希表
思路:
开放寻址法只利用一个数组h[n]
一般h[n]开成要存数据个数的两倍
通过同样的方式找到下标k
如果k中已经存了数据,那么向后寻找直到找到空位将x存进去
#include<iostream>
#include <cstring>
using namespace std;
const int N=200003,null=0x3f3f3f3f; //数组开成两倍,取质数200003 将数组元素初始化成0x3f3f3f3f(无穷大)
int h[N];
int find(int x) //find操作是核心操作,如果用于插入操作,find返回应该插入位置的下标
{ //如果用于查找操作,find返回x的位置下标
int k=(x % N + N) % N;
while(h[k]!=x&&h[k]!=null){ //如果目标位置存在元素且不是x,往下找
k++;
if(k==N)k=0; //找到最后一个则跳转从头开始
}
return k; //返回下标
}
int main(){
memset(h,0x3f,sizeof h);
int n,x;
scanf("%d",&n);
char op[2];
while(n--)
{
scanf("%s%d",op,&x);
int t=find(x);
if(op[0]=='I'){
h[t]=x;
}
else
{
if(h[t]==null)printf("No\n");
else printf("Yes\n");
}
}
return 0;
}
0x3f3f3f3f还能给我们带来一个意想不到的额外好处:如果我们想要将某个数组清零,我们通常会使用memset(a,0,sizeof(a))这样的代码来实现(方便而高效),但是当我们想将某个数组全部赋值为无穷大时(例如解决图论问题时邻接矩阵的初始化),就不能使用memset函数而得自己写循环了(写这些不重要的代码真的很痛苦),我们知道这是因为memset是按字节操作的,它能够对数组清零是因为0的每个字节都是0,现在好了,如果我们将无穷大设为0x3f3f3f3f,那么奇迹就发生了,0x3f3f3f3f的每个字节都是0x3f!所以要把一段内存全部置为无穷大,我们只需要memset(a,0x3f,sizeof(a))
例题 2 字符串哈希
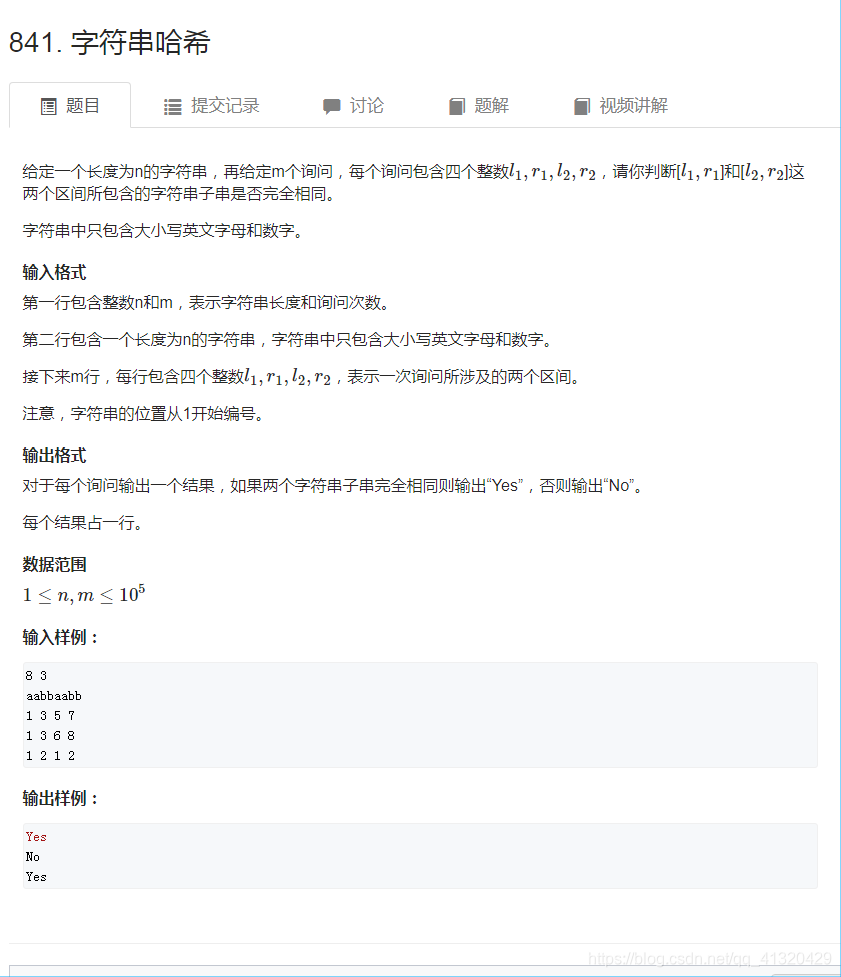
将字符串映射到数组中
例:
- h[0]存0 , h[1]存字符串A哈希值 , h[2] 存字符串AB哈希值
如何将字符串转化成哈希值?
假定p进制数,字符A映射成1,字符B映射成2(实际使用他们的ascll码)- 那么AB表示为
由于最后我们计算出来的哈希值可能非常大,需要让结果%Q(较小的数)- 注意不能将字符映射成0,如将A映射成0,那么导致AA,AAA哈希值全部是0,只要将0特殊化即可
- 一般请况下,只需要将p取131(1331),Q取2^64即可避免99%的冲突
- 因为已经处理出字符串所有前缀的哈希值,只要通过前缀和的方式即可以判断出区间[L,R]中的字符串是否相同
- 求出区间[L,R]的字母的哈希值:
- 定义unsigned long long 数组,当溢出时相当于自动模2^64


#include<iostream>
using namespace std;
typedef unsigned long long ULL;
const int N= 1e5+10 , P=131; //p取131或1331可以有效避免哈希值重复的冲突(99%)
char str[N];
ULL h[N],p[N]; //定义无符号整形数组,当数值溢出时相当于自动%2^64,p数组存放get函数需要用到的乘方值
ULL get (int l,int r){
return h[r]-h[l-1]*p[r-l+1];
}
int main(){
int n,m;
scanf("%d%d",&n,&m);
scanf("%s",str+1);
p[0]=1; //第一个数初始化为1,h[0]默认为0,h[1]存放第一个字符哈希值h[2]存放前两个字符哈希值
for(int i=1;i<=n;i++){
h[i]=h[i-1]*P+str[i];
p[i]=p[i-1]*P; //p[0]=1,p[1]=p,p[2]=p^2,p[3]=p^4....
}
while(m--){
int l1,r1,l2,r2;
scanf("%d%d%d%d",&l1,&r1,&l2,&r2);
if(get(l1,r1)==get(l2,r2))cout<<"Yes"<<endl; //如果两段的哈希值相同,那么这个字符串相同
else cout<<"No"<<endl;
}
return 0;
}
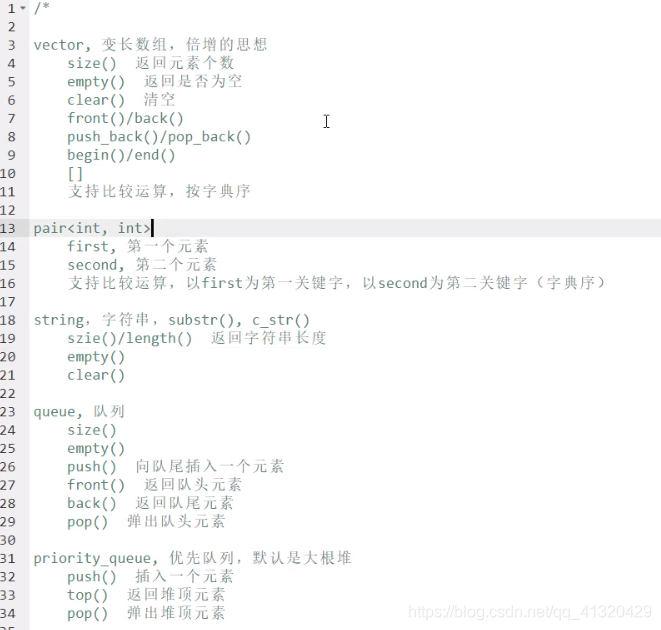
STL 简介





 浙公网安备 33010602011771号
浙公网安备 33010602011771号