数学知识(数论一)
数学知识(数论一)
质数

思路:把1~根号n之间的数都找一遍,看看有没有一个数是n的因子,之所以找到根号n,是因为因子都是成对出现的,假设i是n的因子,且
i<sqrt(n),那么i必定存在另外一个因子x>sqrt(n),所以只需要找到较小的因子即可
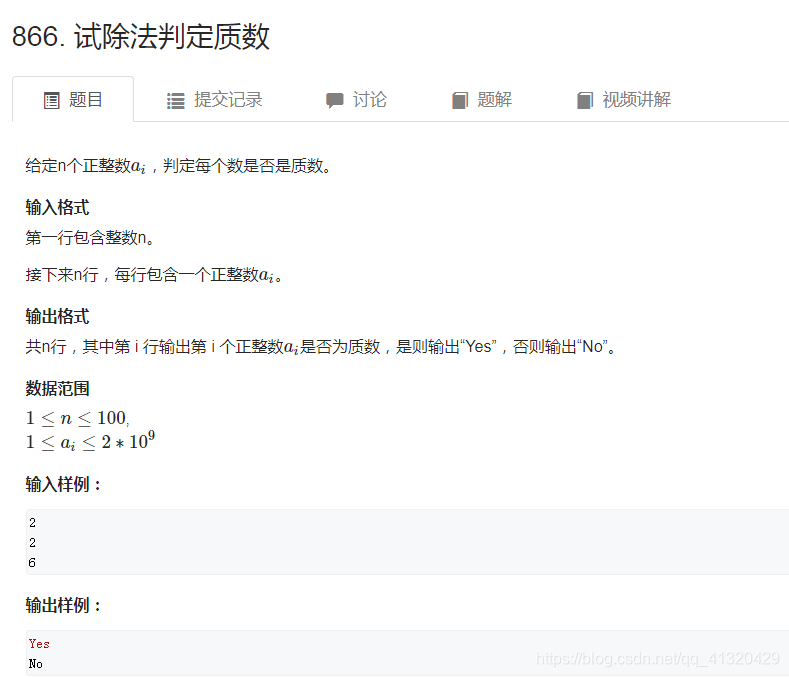
866试除法判定质数
#include<iostream>
#include<algorithm>
using namespace std;
int n;
bool is(int x){
if(x<2)return false;
for(int i=2;i<=x/i;i++){ //注意这里不建议写i<=sqrt(x)这样会调用sqrt函数,使效率下降,写i*i<=x可能会溢出
if(x%i==0)return false;
}
return true;
}
int main(){
cin>>n;
while(n--){
int x;
cin>>x;
if(!is(x))cout<<"No"<<endl;
else cout<<"Yes"<<endl;
}
return 0;
}
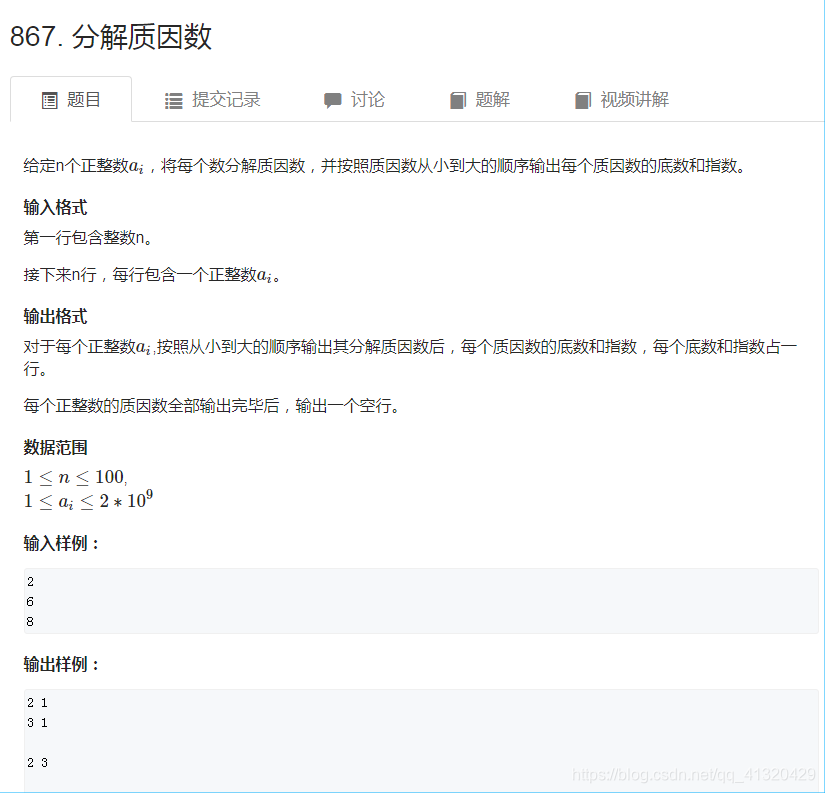
867分解质因数
- 思路:
- 从2开始试除,x每能整除i时将i“除干净”(因此会将x的合数因子提前除干净,枚举剩下的就是质因子)
- 统计i的指数次数,并依次试除直到sqrt(x),如果x仍然大于1,输出最后一个大于sqrt(x)的质因数(有且只有一个)
#include<iostream>
#include<algorithm>
using namespace std;
int n;
void divide(int x){
for(int i=2;i<=x/i;i++){
if(x%i==0){
int s=0; //统计该因数的指数
while(x%i==0){
s++;
x/=i;
}
printf("%d %d\n",i,s);
}
}
if(x>1)printf("%d %d\n",x,1); //最多只有一个大于sqrt(x)的质数且他的指数是1,(有两个就大于x了)
}
int main(){
cin>>n;
while(n--){
int x;
cin>>x;
divide(x);
printf("\n");
}
}
868筛质数
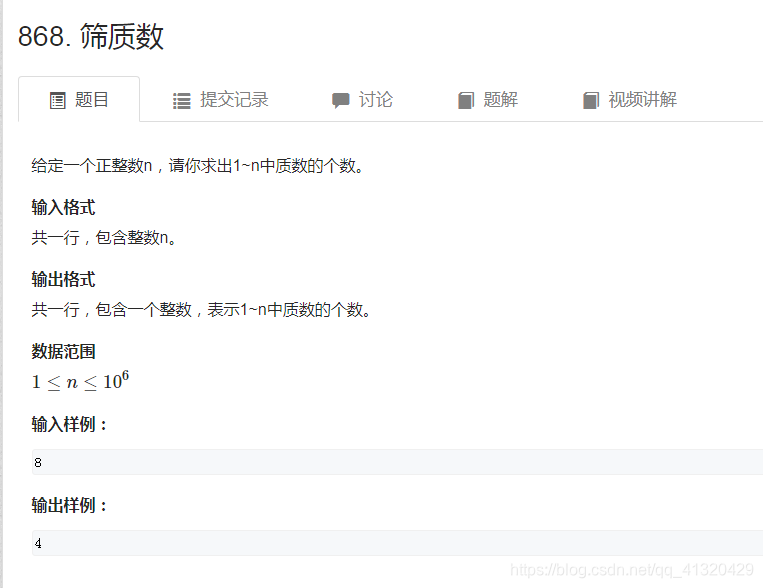
(一)朴素筛法:
- 枚举2~n
- 从2开始将它们的倍数(
2,4,6...)从st数组里面全部删除- 如果枚举到一个数
p它仍然在st里(没有被删除)说明它是个质数(没有1~p-1的因子)- 时间复杂度(n/2+n/3+n/4+…n-1/n+n/n)(
调和级数)——删2的倍数,3的倍数,4的倍数…
=nlnn≈nlogn
优化:只需要删除质数的倍数即可
质数定理:1~n中只有
n/lnn个质数
时间复杂度:近似为O(n)实际为O(nloglogn)

//朴素优化
#include <iostream>
#include<algorithm>
using namespace std;
const int N =1e6+10;
int n;
int cnt;
int st[N],primes[N];
//朴素优化版
void get(int x){
for(int i=2;i<=x;i++){
if(!st[i])primes[cnt++]=i;
for(int j=i+i;j<=x;j+=i)st[j]=true; //把素数的所倍数删除
}
}
int main(){
cin>>n;
get(n);
cout<<cnt;
return 0;
}
(二)线性筛法:
- 保证
每个和数都是被他的最小质因子筛掉,
例如:10会被2筛掉而不是被5筛掉,这样保证每个数只会被删除一次,- 时间复杂度
O(n)- 在
n>10^7的时候会比朴素法快一倍,小于10^7的时候差不多
思路:枚举i=2~n
保证每个i都被它的最小质因子筛掉(primes[j]质数数组)
当枚举到i时st数组里仍然存在i,说明i是质数,加入primes数组
对于每个i,枚举primes[j]
删除st[primes[j]*i](保证这个被删除的数是被它的最小质因子删除的)

判断如果i%primes[j]==0 说明primes[j]已经枚举到i的最小质因子了,跳出
#include <iostream>
#include<algorithm>
using namespace std;
const int N =1e6+10;
int n;
int cnt;
int st[N],primes[N];
//线性法
void get(int n){
for(int i=2;i<=n;i++){
if(!st[i])primes[cnt++]=i;
for(int j=0;primes[j]<=n/i;j++){ //删的最大的数(primes[j]*i)不能超过n
st[primes[j]*i]=true; //每次把primes[j]*i删除
if(i%primes[j]==0)break; //已经枚举到了i的最小质因子,此时说明i已经被他的最小质因子删除了(i==2的时候pj等于2跳出(此时删除4),i等于4的时候pj等于2跳出(此时删除8),6的时候pj等于2跳出,9的时候pj等于3跳出....)
}
}
}
int main(){
cin>>n;
get(n);
cout<<cnt;
return 0;
}
约数
所有int范围内,约数最多的一个数大约有1500个约数

每一个数N可以表示成一个连乘积的形式p1^a1*p2 ^a2…
他的约数d也可以表示成这种形式
每一项p都有0~ai种选法,所以有上面的约数个数公式
从每一项中选一个p组成连乘积,他们的和就是约数之和,有上面的约数之和的公式
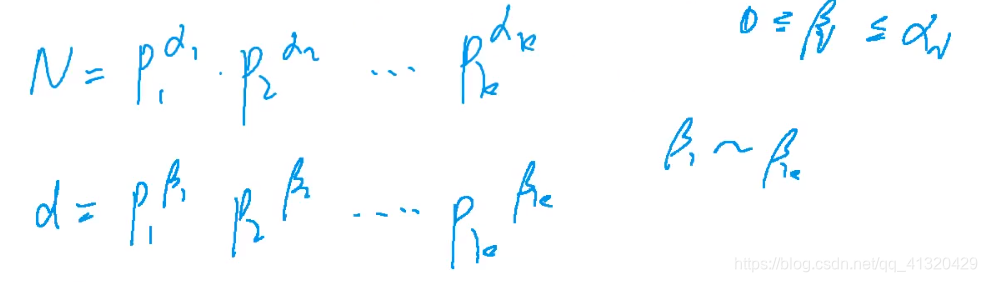
869试除法求约数
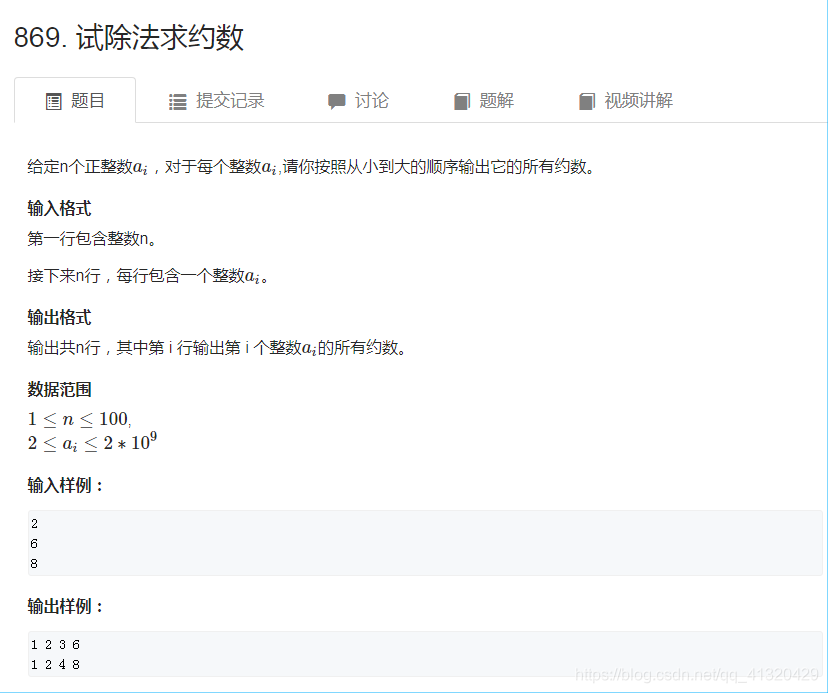
#include<vector>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
vector<int> primes;
int n;
void get(int x){
primes.clear();
for(int i=1;i<=x/i;i++){ //从1枚举到sqrt(n)
if(x%i==0){
primes.push_back(i);
if(i!=(x/i))primes.push_back(x/i); //如果另一个约数和i不相等,加入primes
}
}
sort(primes.begin(),primes.end());
}
int main(){
cin>>n;
while(n--){
int x;
cin>>x;
get(x);
for(auto prime:primes)cout<<prime<<" ";
cout<<endl;
}
return 0;
}
870约数个数
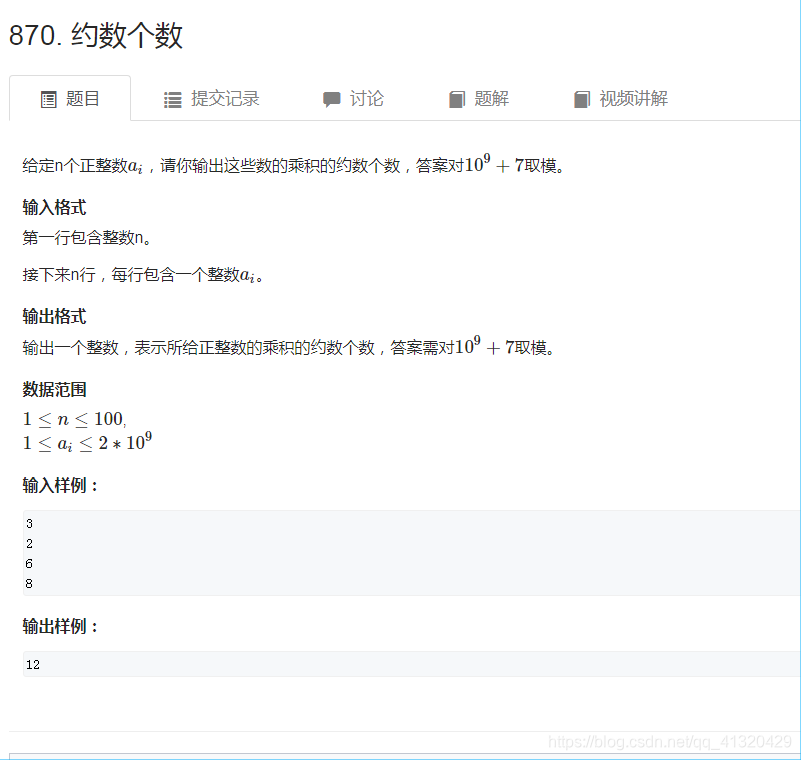
思路:只要将这些数挨个表示成连乘积的形式,保留每一项的底数和指数,最后使指数相乘即可
#include<iostream>
#include<cstring>
#include<algorithm>
#include<unordered_map>
using namespace std;
const int N=110,mod=1e9+7;
typedef long long LL;
int n;
int main(){
cin>>n;
unordered_map <int,int> primes; //无序键值对 unordered_map<key,value>key是底数 value是指数
while(n--){
int x;
cin>>x;
for(int i=2;i<=x/i;i++){ //分解质因数
while(x%i==0){
x=x/i;
primes[i]++;
}
}
if(x>1)primes[x]++; //最后一个可能的质因子
}
LL res=1;
for(auto prime:primes){
res=res*(prime.second+1)%mod; //每乘一个数都mod,遍历到prime等于0相当于乘1
}
cout<<res;
}
871约数之和
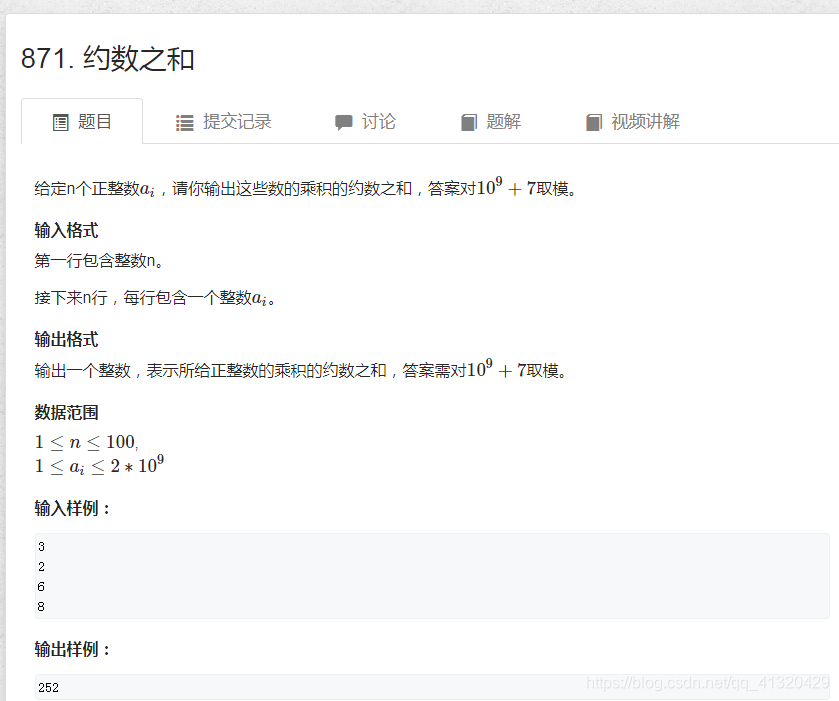
#include<iostream>
#include<cstring>
#include<algorithm>
#include<unordered_map>
using namespace std;
const int mod=1e9+7;
typedef long long LL;
int n;
int main(){
cin>>n;
unordered_map <int,int> primes; //无序键值对 unordered_map<key,value>key是底数 value是指数
while(n--){
int x;
cin>>x;
for(int i=2;i<=x/i;i++){ //分解质因数
while(x%i==0){
x=x/i;
primes[i]++;
}
}
if(x>1)primes[x]++; //最后一个可能的质因子
}
LL res=1;
for(auto prime:primes){
int p=prime.first,a=prime.second;
LL s=1; //s=p^a+p^a-1+......p^1+p^0;
for(int i=1;i<=a;i++)
s=(s*p+1)%mod; //防止每一项溢出
res=res*s%mod;
}
cout<<res;
}
872最大公约数
a与b的最大公约数c也是a%b的公共约数
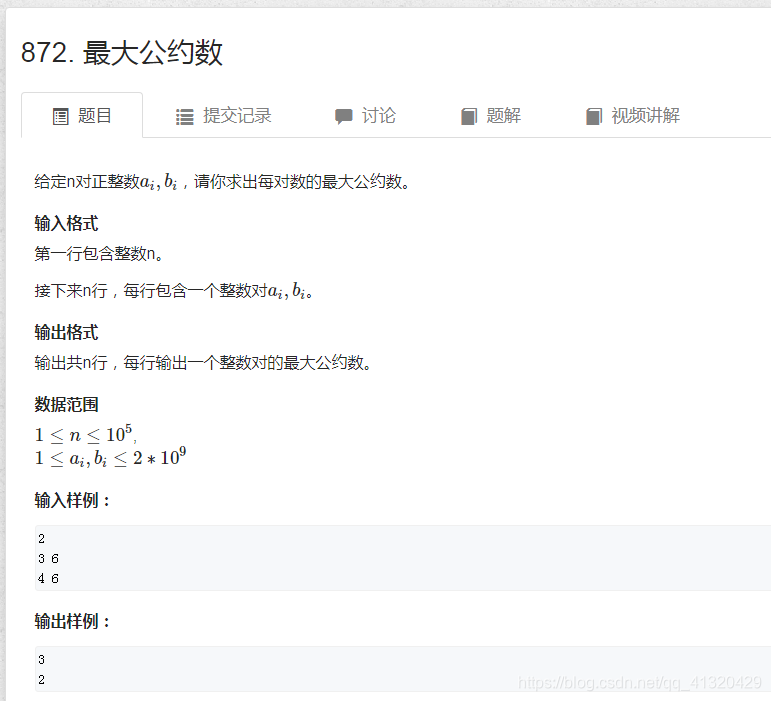
#include<iostream>
#include<algorithm>
using namespace std;
int n;
int gcd (int a,int b){
return b ? gcd(b,a%b):a;
}
int main(){
cin>>n;
while(n--){
int a, b;
cin>>a>>b;
cout<<gcd(a,b);
cout<<endl;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号