数学知识(数论二)

文章目录

• 数论（二）
• 欧拉函数
• 873欧拉函数
• 874筛法求欧拉函数
• 快速幂
• 875快速幂（O（logn））
• 876快速幂求逆元(a与p互质时才能使用)
• 拓展欧几里得算法
• 877拓展欧几里得算法
• 878线性同余方程
• 中国剩余定理
• 204表达整数的奇怪方式

数论（二）

欧拉函数

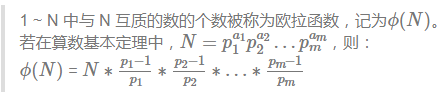
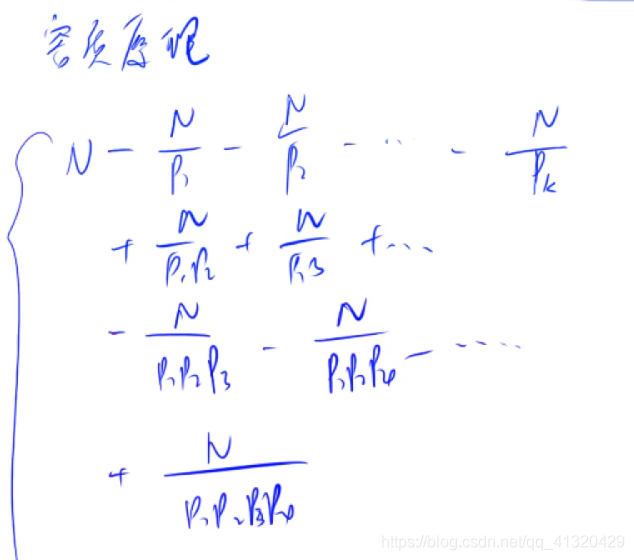
容斥原理：求1~n中与n互质的数，需要将n的质因子的倍数全部删除
如果多删要加回来，有下面的公式：
等同于上面的φ(n)；

欧拉函数最坏情况下的大小为N^2

873欧拉函数

#include<iostream>
#include <algorithm>
#include<cstring>

using namespace std ;

const int N=2*1e9+10;

int n;



int main(){

cin>>n;

while(n--){
    
    int a;
    
    cin>>a;
    
    int  res=a;
    
    for(int i=2;i<=a/i;i++){
        
        if(a%i==0)
        {
            while(a%i==0)a=a/i;
            
            res=res/i*(i-1);   //这里先除以i再乘i-1防止数据溢出
            
        }
        
        
    }
    
    
    if(a>1)res=res/a*(a-1);
    
    cout<<res<<endl;
    
}
    
}

874筛法求欧拉函数

采用线性筛法，在筛选过程中求每一个数的欧拉函数，时间复杂度降低为n，如果对每一个数分解质因数，复杂度会上升到nsqrt(n)

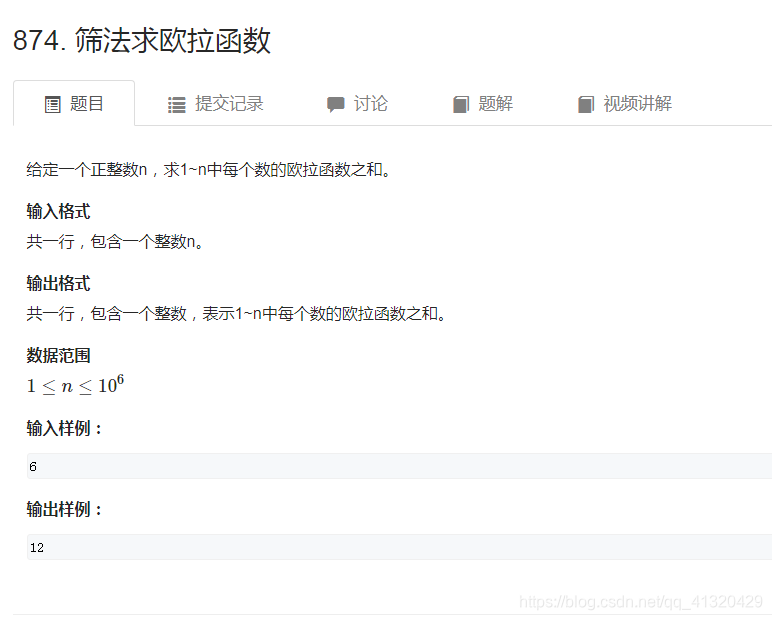
思路：线性筛法：
遍历i=2~n （1的欧拉函数是1）
如果遍历到的i是质数，那么euler[i]=i-1，并把i加入pj
对于每一个i，遍历pj，筛掉所有的pj*i
并且如果

• i%pj==0 那么euler[pj *i]=pj *euler[i]
• i%pj!=0 那么euler[pj *i]=(pj-1) *euler[i]
  详细证明如下图

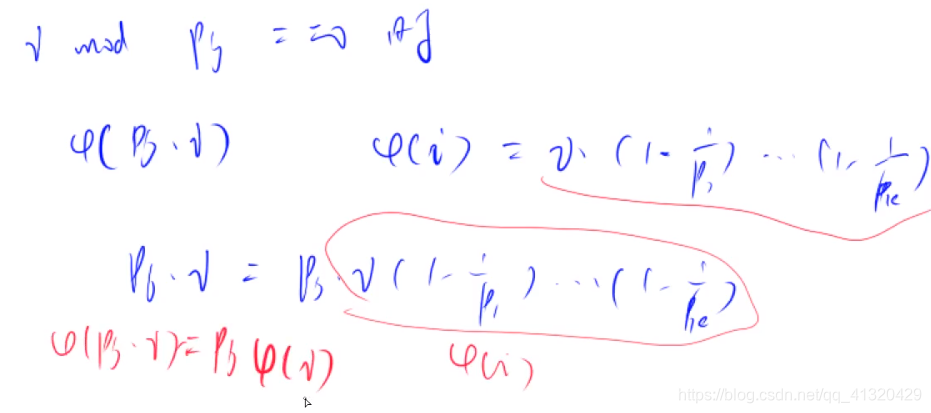
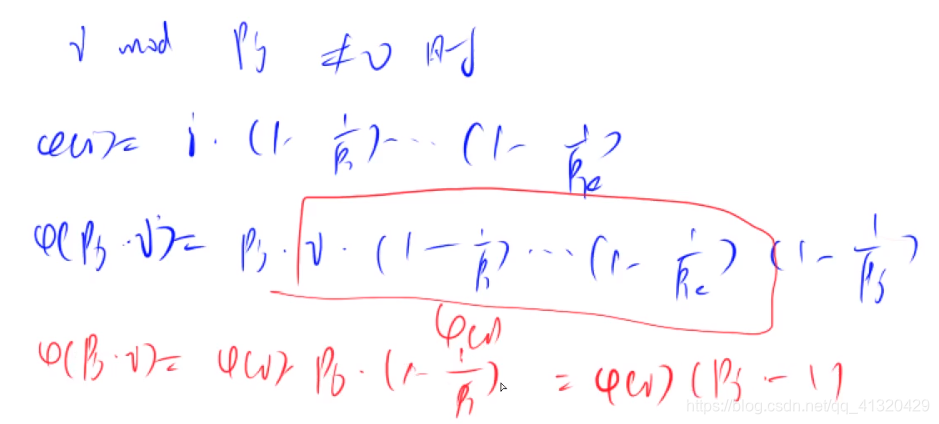
#include<iostream>
#include<algorithm>

using namespace std;

const int N=1e6+10;

typedef long long LL;

int n,cnt;

bool st[N];             //状态st

int euler[N];           //欧拉函数

int primes[N];          //质数数组

LL get_euler(int n){
    
    LL res=0;
    
    euler[1]=1;          //1的欧拉函数是1
    
    for(int i=2;i<=n;i++){
        
        if(!st[i]){
            
            primes[cnt++]=i;
            
            euler[i]=i-1;      //i是质数，它对应的欧拉函数是i-1
        }
        
        
        //遍历所有质数，并对1~n中合数求欧拉函数
        for(int j=0;primes[j]*i<=n;j++){
            
            st[primes[j]*i]=true;
            
            if(i%primes[j]==0){
                
                euler[primes[j]*i]=primes[j]*euler[i];    //pj是i的最小质因数，此时φ(pj*i)=pj*φ(i);
                
                break;
                
            }
            
            else euler[primes[j]*i]=(primes[j]-1)*euler[i];  //如果不是，公式φ(pj*i)=(pj-1)*φ(i)
            
        }
        
    }
    
    for(int i=1;i<=n;i++){                         
        
        res+=euler[i];
    }
    
    return res;
}



int main(){
    
    cin>>n;
    
    cout<<get_euler(n);
    
    return 0;
}

---

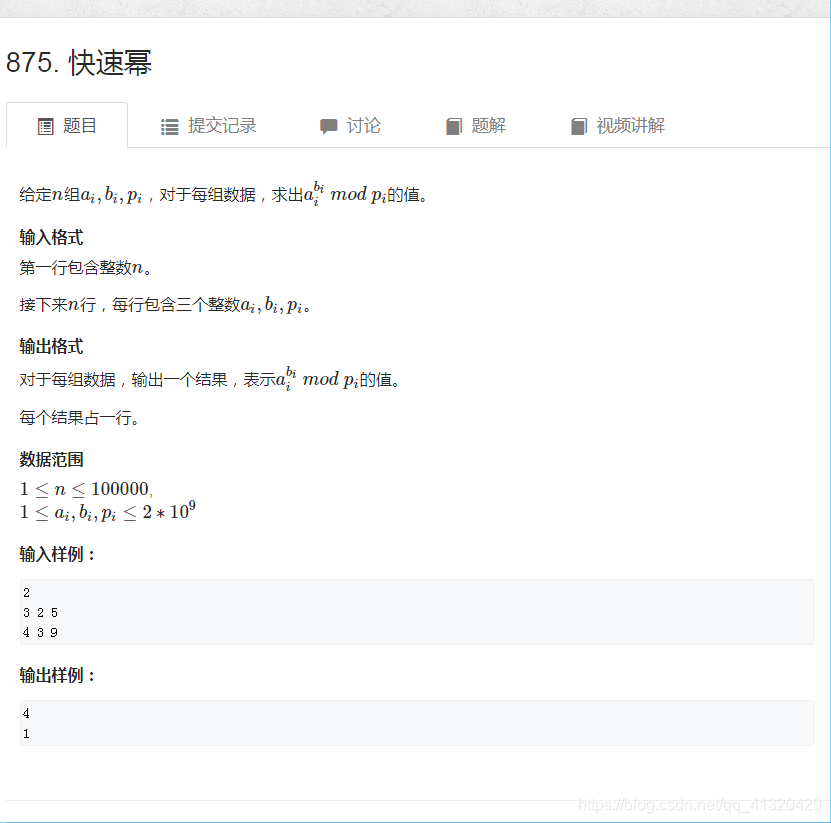
快速幂

快速的求出a^k mod p的值
1<=a,k,p<=1e9+10

• 正常循环求复杂度为O(k)
• 时间复杂度降为k 转化成二进制后的位数O(logk)
  思路：
• 首先把k拆成2进制表示的形式$k=2^{x1}+ 2 ^{x2}+...$
• 预处理出所有$a^{2^0},a^{2^1} ....mod p$的值
• 最后a^k 用这些数的乘积再mod p表示如图所示：

其中预处理数耗时logk 最后乘出a^k 耗时logk 时间复杂度为logk

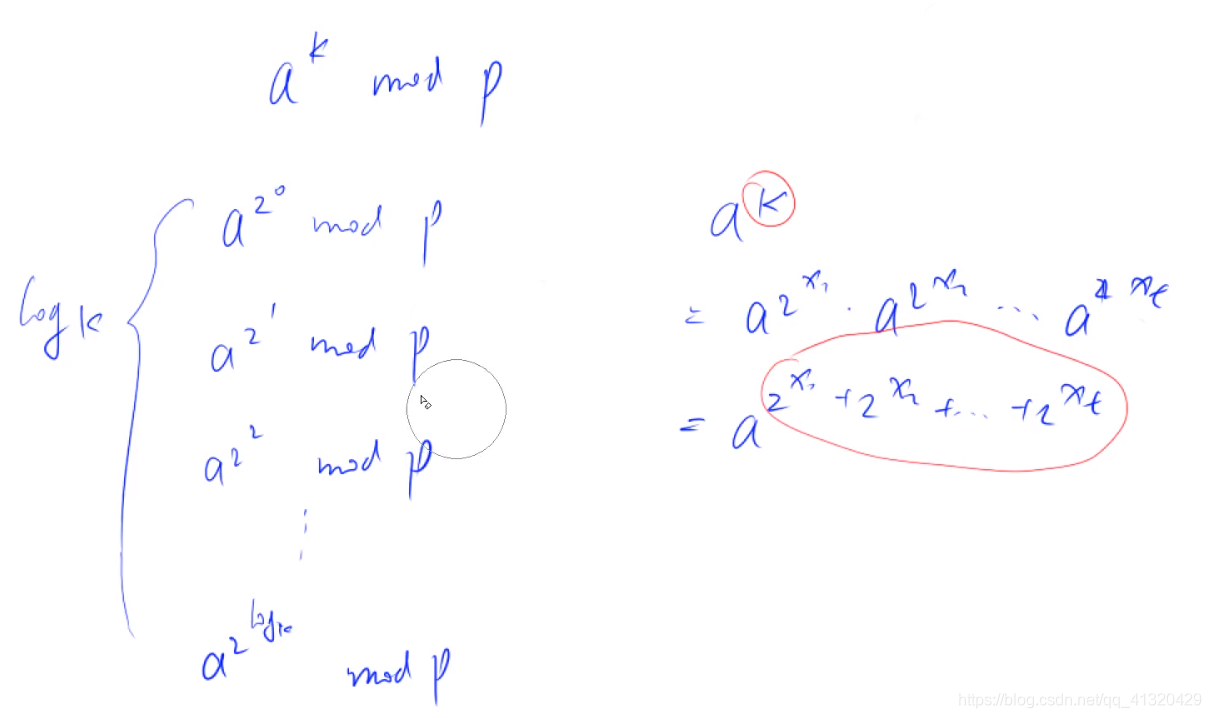
举例说明：

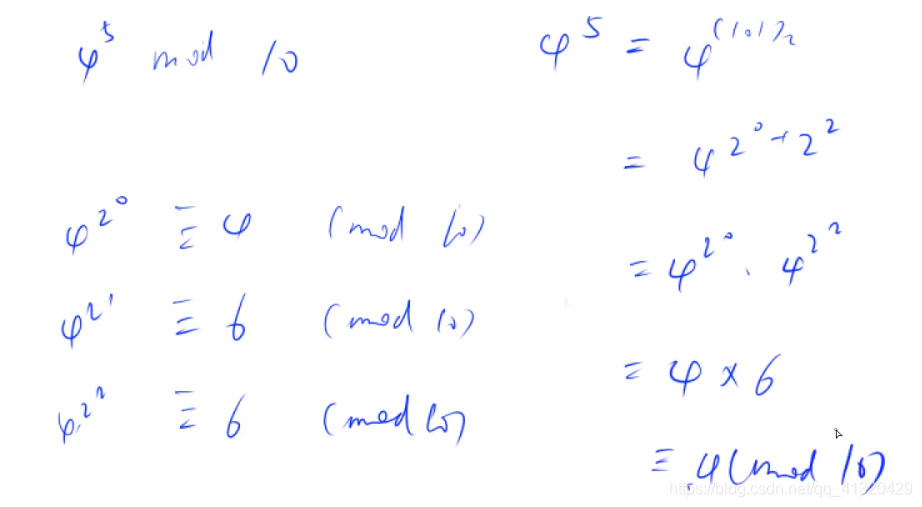
预处理过程：
每一个数都是前一个数的平方mod p

• 即已知$a \ mod \ p$
• 求$a^2\ mod\ p$
• $a^2 \ mod \ p == (a \ mod \ p)^2 \mod \ p$

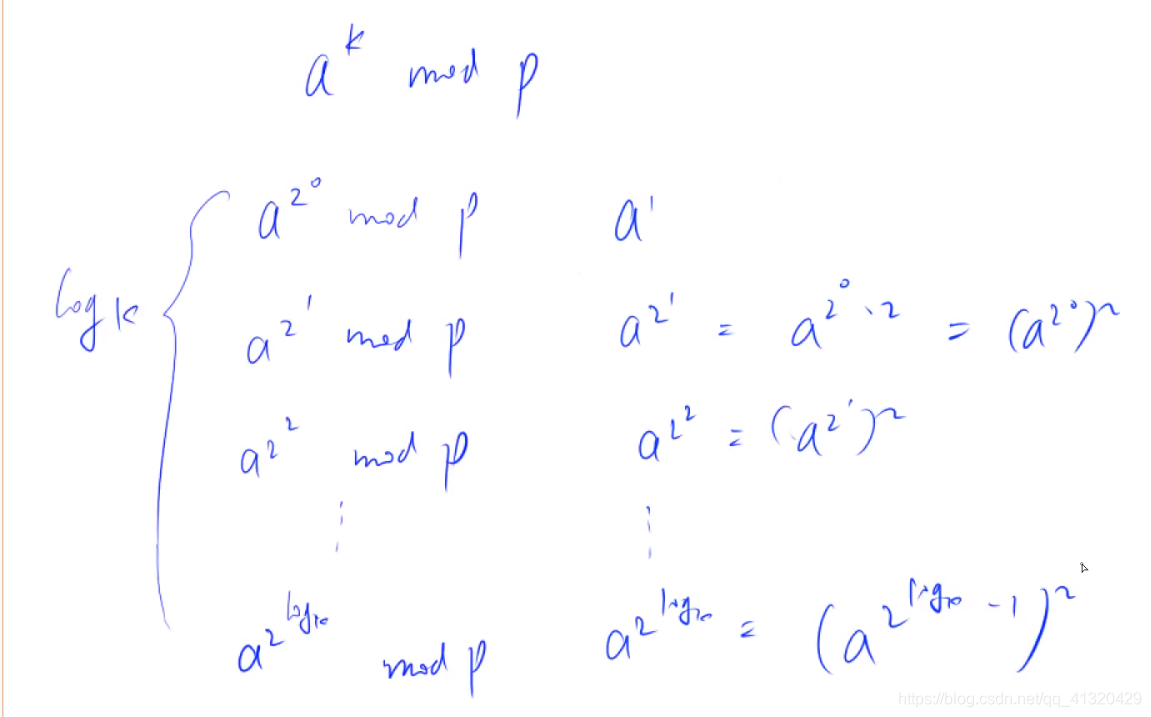
875快速幂（O（logn））

#include<iostream>
#include<algorithm>

using namespace std;

typedef  long long LL;                //在乘的过程中可能会溢出，需要强转

const int N=2*1e9+10;

int qmi(int a,int k,int p){
    
    int res=1;                         //res在p以内，不会超出int
    
    while(k){
        
        if(k&1)res=(LL)res*a%p;        //将k转2进制，k&1表示当k的当前位等于1，将当前a乘进结果   res*a可能会溢出，强转一下
        
        k=k>>1;                       //k右移一位
        
        a=(LL)a*a%p;                  //更新a的值       同理a*a可能也会溢出，强转一下（LL赋值给int取低四个字节，这里没有溢出，所以值不变）
    }
    
    return res;
    
}


int main(){
    
    int n;
    
    scanf("%d",&n);
    
    while(n--){
        
        int a,k,p;
        
        scanf("%d%d%d",&a,&k,&p);
        
        printf("%d\n",qmi(a,k,p));
        
    }
    
    return 0;
}

876快速幂求逆元(a与p互质时才能使用)

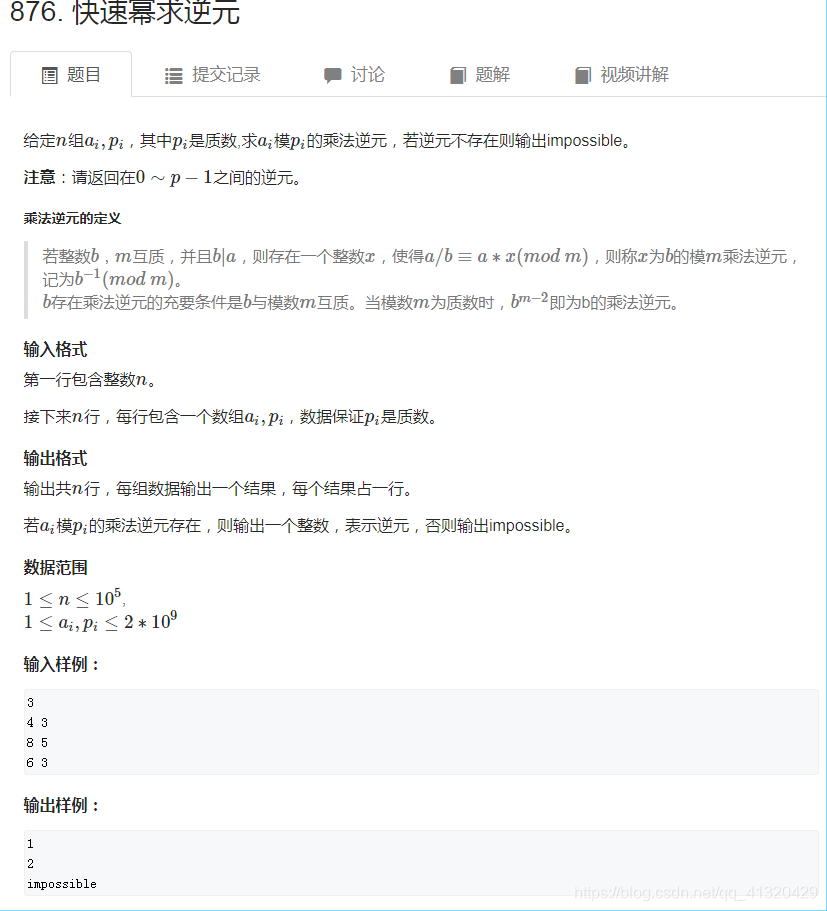
• 分析题干
• 求b的逆元，存在一个整数a使得$a/b \ mod \ m$与$a*x \ mod \ m$相等
• 把x叫做b的逆元记$x=b^{-1}$

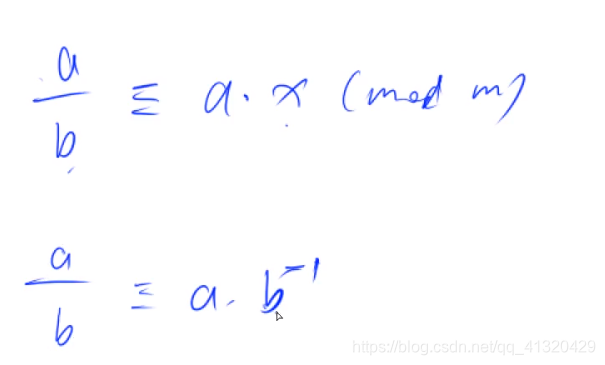
推出逆元的性质：

• $b* b^{-1} mod \ m =1$
  那么求逆元即找到一个数与b的乘积mod m等于1（m与b互质）
• 由费马定理
  $b^{m-1}\ mod \ m=1$ （b与m互质)
  $b*b^{m-2} \ mod \ m=1$
• 所以$b^{-1} =b^{m-2}$

#include<iostream>
#include<algorithm>

using namespace std;

const int N=2*1e9+10;

typedef  long long LL;

int qmi(int a,int k,int p){
    
    int res=1;
    
    while(k){
        
        if(k&1)res=(LL)res*a%p;
        
        k=k>>1;
        
        a=(LL)a*a%p;
        
    }
    
    return res;
}


int main(){
    
    int n;
    
    cin>>n;
    
    while(n--){
        
        int a,p;
        
        cin>>a>>p;
        
        int res=qmi(a,p-2,p);
        
        if(a%p)cout<<res<<endl;             //输入的p如果与a互质，那么输出结果
        
        else  cout<<"impossible"<<endl;
    }
    
    return 0;
}

拓展欧几里得算法

裴蜀定理：对于任意一对正整数a，b，一定存在一对非零x，y使得ax+by=gcd（a，b）

思路：利用标准gcd算法，过程中递归求出系数xy
分两种情况

• 边界：当递归到最后的边界时有（a，0）此时返回公约数a，，，x，y对应的值分别是1,0
• 常规情况：递归调用exgcd（b，amodb，y，x），此时递归结束后x，y的值应当被更新成当前调用的值，对应关系推导如图
  x=x
  y=y-(a/b) * x 意味着y的值会变小，符合实际情况

注意x,y的值不唯一

$\because ax+by =gcd(a,b)$等价于$by+(a\%b)x=gcd(a,b)$

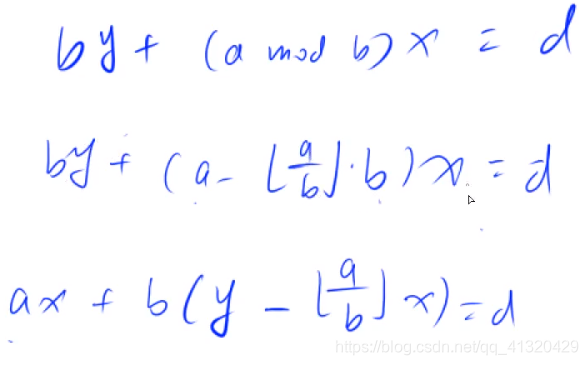
若对于a，b，解得一组解$x_0,y_0$
下面是对应$ax+by=d$的完全解：
$x=x_0-b/d*k$
$y=y_0+a/d*k$

？为什么完全解不写为
$x=x_0-b*k$
$y=y_0+a*k$
因为d是从a，b中分离，去掉/d会丢掉很多解

877拓展欧几里得算法

#include<iostream>
#include<algorithm>

using namespace std;

const int N=1e5+10;
                           
int exgcd(int a,int b,int & x,int & y){
    
    if(!b){
        
        x=1,y=0;
    
        return a;
    }
    
    
    int d= exgcd(b,a%b,y,x);          //此步要颠倒一下对应系数 
    
    y-=a/b*x;                         //更新y的值，x的值不变
    
    return d;
    
}


int main(){
    
    int n;
    
    cin>>n;
    
    while(n--){
        
        int a,b,x,y;
        
        cin>>a>>b;
        
        exgcd(a,b,x,y);
        
        cout<<x<<" "<<y<<endl;
        
    }
    
    
}

878线性同余方程

分析：问题の转化：
由题干$ax \equiv b(mod m)$
可知ax可以表示为my+b

• $\because$ $ax \% m= b \% m$
• $(my +b) \% m=b \% m$
• $\therefore$ $ax=my+b$

移项得：
$ax+my'=b（y'=-y）$
问题到此转化为已知a，m求系数x，y’使得$ax+my'=b$
由拓展欧几里得可求$ax+my=gcd（a，m）=d$
即$b=kd, k\in Z$时，存在解

求解结束时输出a的系数x mod m（不爆范围）即可

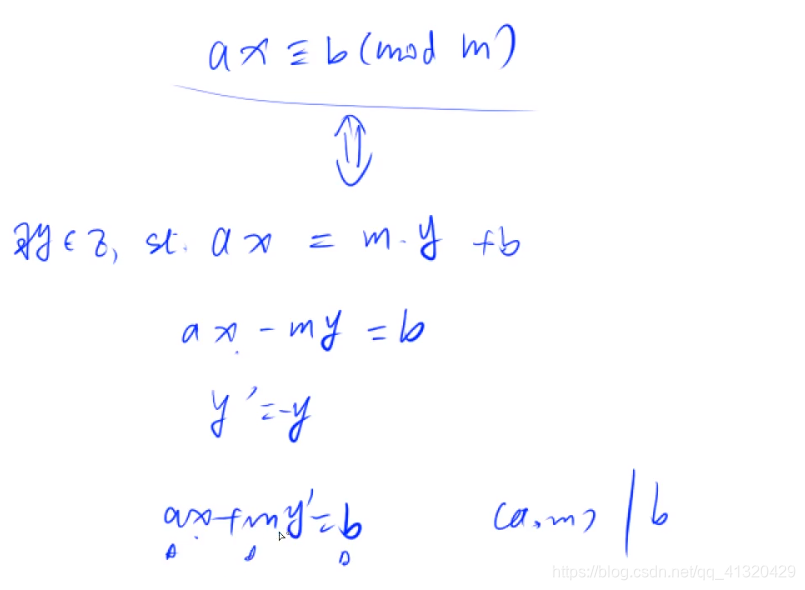
#include<iostream>
#include<algorithm>

using namespace std;

typedef long long LL;

int exgcd(int a,int b,int &x,int &y){
    
    if(!b){
        
        x=1,y=0;
        
        return a;
        
    }
    
    int d=exgcd(b,a%b,y,x);
    
    y-=a/b*x;
    
    return d;
    
}


int main(){
    
    int n;
    
    cin>>n;
    
    while(n--){
        
        int a,b,m;
        
        int x,y;
        
        cin>>a>>b>>m;
        
        int d=exgcd(a,m,x,y);
        
        if(b%d)cout<<"impossible"<<endl;     //b不是d的倍数，不存在x
        
        else {
            
            x=(LL)x*(b/d)%m;                //模m防止溢出
            
            cout<<x<<endl;
            
        }
    }
    
    return 0;
    
}

中国剩余定理

摘自百度百科

最终解为：

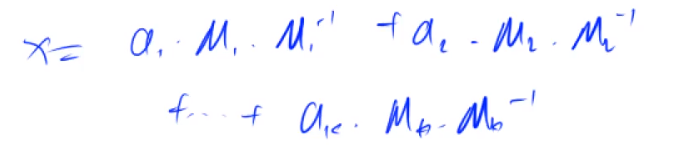
因为a和M不一定满足互质条件
所以不用费马定理的快速幂求逆元
而采用线性同余方程$M_ix \equiv b(\% m)$求逆元
此时b应当等于1
即$M_ix\%m =1$
转化为拓展欧几里得：$M_ix +my=gcd(a,m)=d$
1应当为d的整数倍

204表达整数的奇怪方式

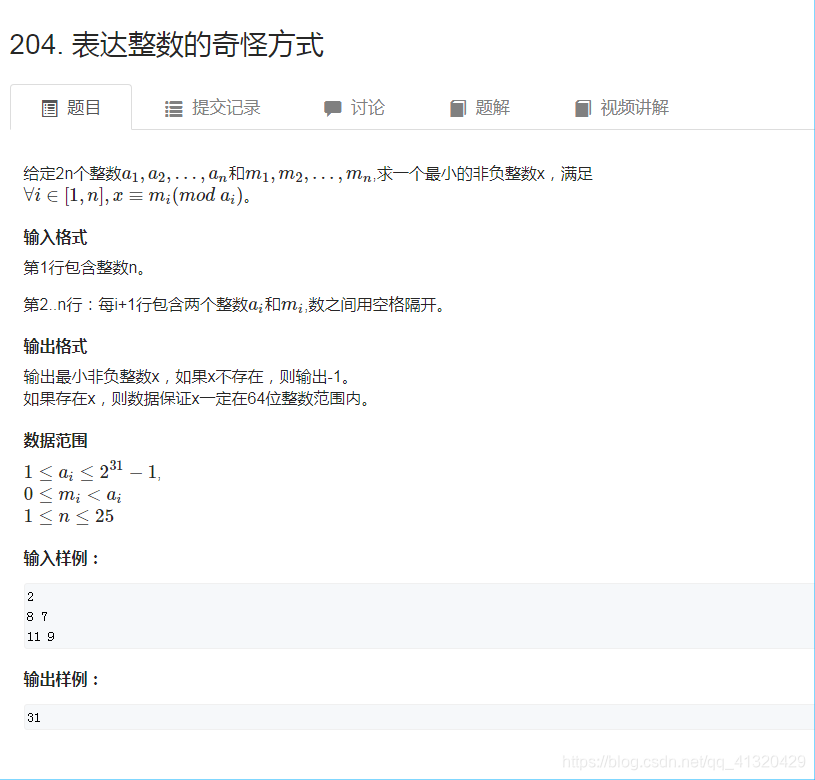
该题不满足中国剩余定理两两互质的条件
公式の推导：

• 要满足一元线性同余方程组
  
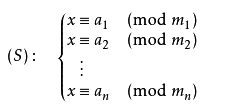
• 任取其中两个式
• $x\equiv a_1(modm_1)$化为$x=k_1m_1+a1$
  $x\equiv a_2(modm_2)$化为$x=k_2m_2+a2$
• 合并得：$k_2m_2-k_1m_1=a_2-a_1$
• 通过拓展欧几里得算法可知当$a_2-a_1=k gcd(m_2,-m_1)=kd$存在时有解
• 当有解时，推得完全解$k_2=k_2+k$ ${m_1}\over{d}$ , $k_1=k_1+k\frac {m_2}{d}$
• 代入上面x可以解得
• $x=k_1m_1+a_1+k$$m_2m_1\over d$
• 令$k_1m_1+a_1=a_0$,$k$$m_2m_1\over d$$(k[m_2,m_1])$（方括号代表最小公倍数）$=km_0$
• 对上面所有线性同余方程两两化简，最后可以得到解$x=km_0+a_0$
• 此时所求答案就是$a_0$取整数（找的就是x的最小正整数解，但是a0可能是负数需要转正）

#include<iostream>
#include<algorithm>

using namespace std;

typedef  long long LL;


LL exgcd(LL a,LL b,LL &x,LL &y){
    
    if(!b){
        
        x=1;
        y=0;
        
        return a;
        
    }
    
    int d=exgcd(b,a%b,y,x);
    
    y-=a/b*x;
    
    return d;
    
} 


int main(){
    
    int n;
    
    cin>>n;
    
    LL a1,m1;
    
    cin>>a1>>m1;
    
    bool  hash_answer=true;
    
    for(int i=0;i<n-1;i++){
        
        LL a2,m2;
        
        cin>>a2>>m2;
        
        LL k1,k2;
        
        int d=exgcd(a1,a2,k1,k2);
        
        if((m2-m1)%d){
            
            hash_answer=false;
            
            break;
            
        }
        
        else{
            
            k1*=(m2-m1)/d;
            
            LL t=a2/d;
            
            k1=(k1%t+t)%t;             //把k1中a2/d的因子全部去除，使k1是满足条件的最小正整数
            
            m1+=a1*k1;
            
            a1=abs(a1/d*a2);          //a1可能是负数，取绝对值
            
        }
        
    }
    
    
    if(hash_answer)cout<<(m1%a1+a1)%a1<<endl;
    
    else  cout<<-1;
    
}