基于人类反馈的强化学习 RLHF

1.强化学习和语言模型的联系

agent: 语言模型本身

state: prompt(input tokens)

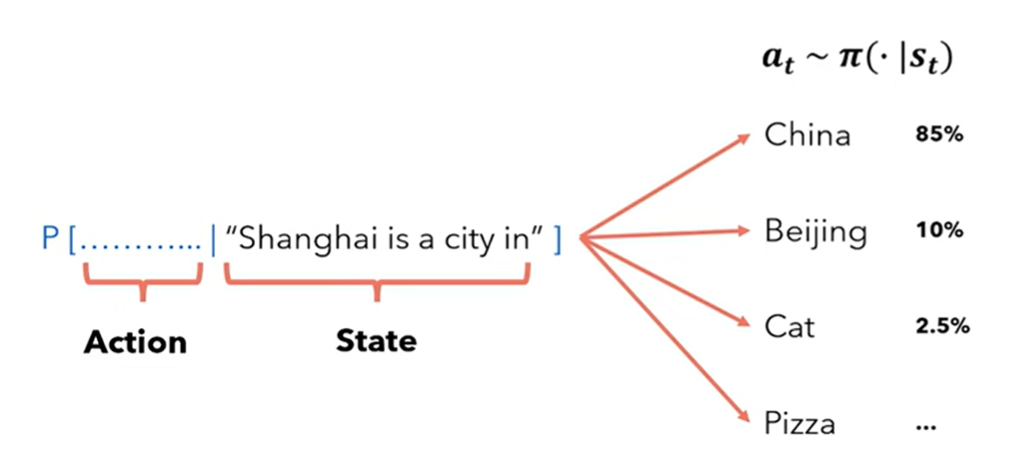
action: 选择哪个token作为下一个token（贪婪，top k,top p）

reward model：当生成‘好的回复’语言模型应当被奖励，当生成‘差的回复’语言模型不会受到任何奖励

policy：语言模型本身，因为它对动作空间给出当前状态的概率进行建模：\({a_t} \sim \pi(·|S_t)\)

2. 语言模型的奖励模型

人类不擅长达成一致，但是我们很擅长比较

2.1 数据集

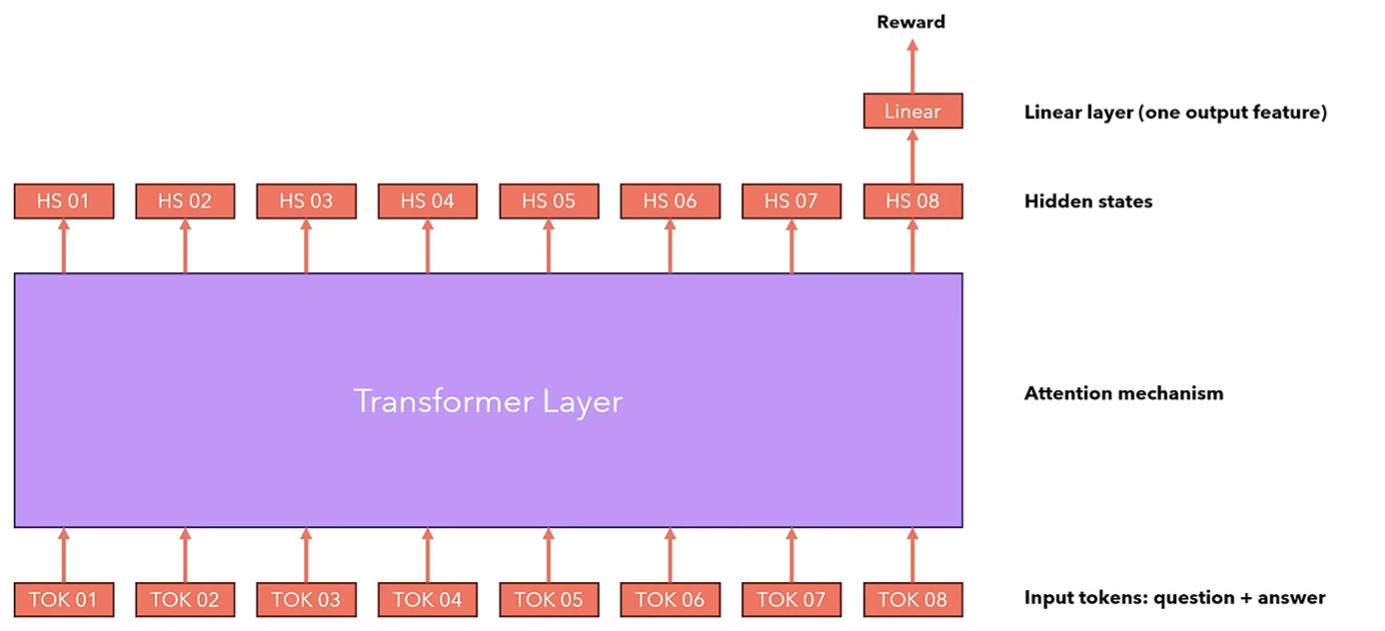
2.2 奖励模型架构

2.3 奖励模型损失

为了借助强化学习优化我们的语言模型表现，我们需要一个打分模型，对语言模型生成的每个回复给予一个数值。
现在我们有一个定义了基于一个query(prompt)下更喜欢的answer的数据集，我们可以搭建一个神经网络，使之可以对每一个response生成一个数字分数。

\[Loss = -log\ \sigma (r(x,y_w) - r(x, y_l)) \]

good answer : \(r(x,y_w)\)
bad answer : \(r(x,y_l)\)

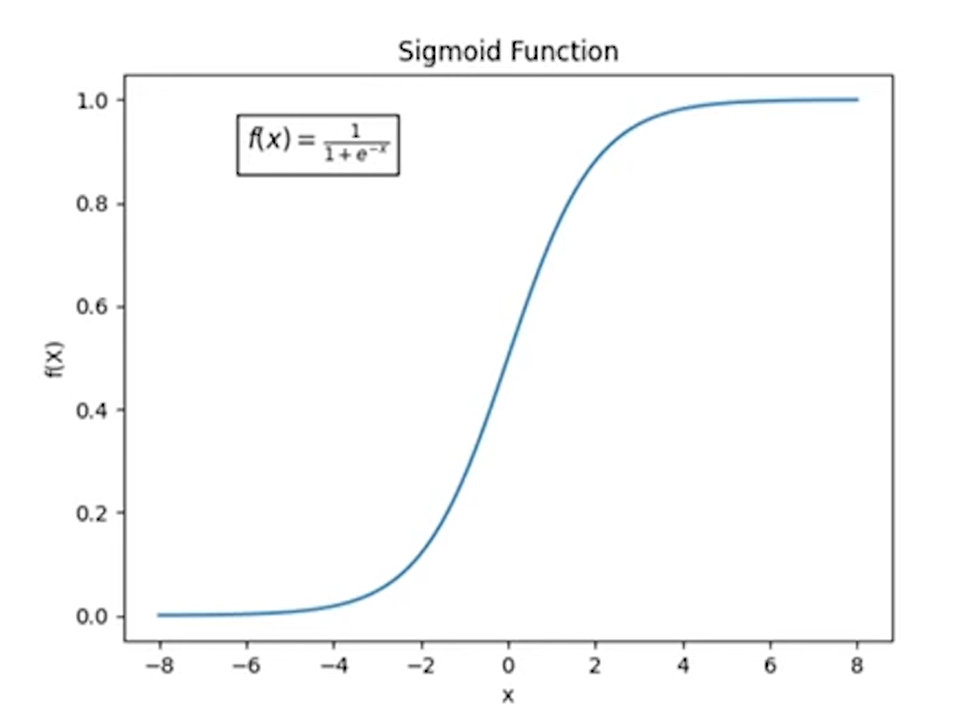
如果 \(r(x,y_w)\) > \(r(x,y_l)\) -> sigmoid会返回一个value > 0.5 -> loss会很小
·如果顺序正确，loss会很小

如果 \(r(x,y_w)\) < \(r(x,y_l)\) -> sigmoid会返回一个value < 0.5 -> loss会很大
·如果顺序错误，loss会很大

Note:
sigmoid函数：

2.4 具体实现

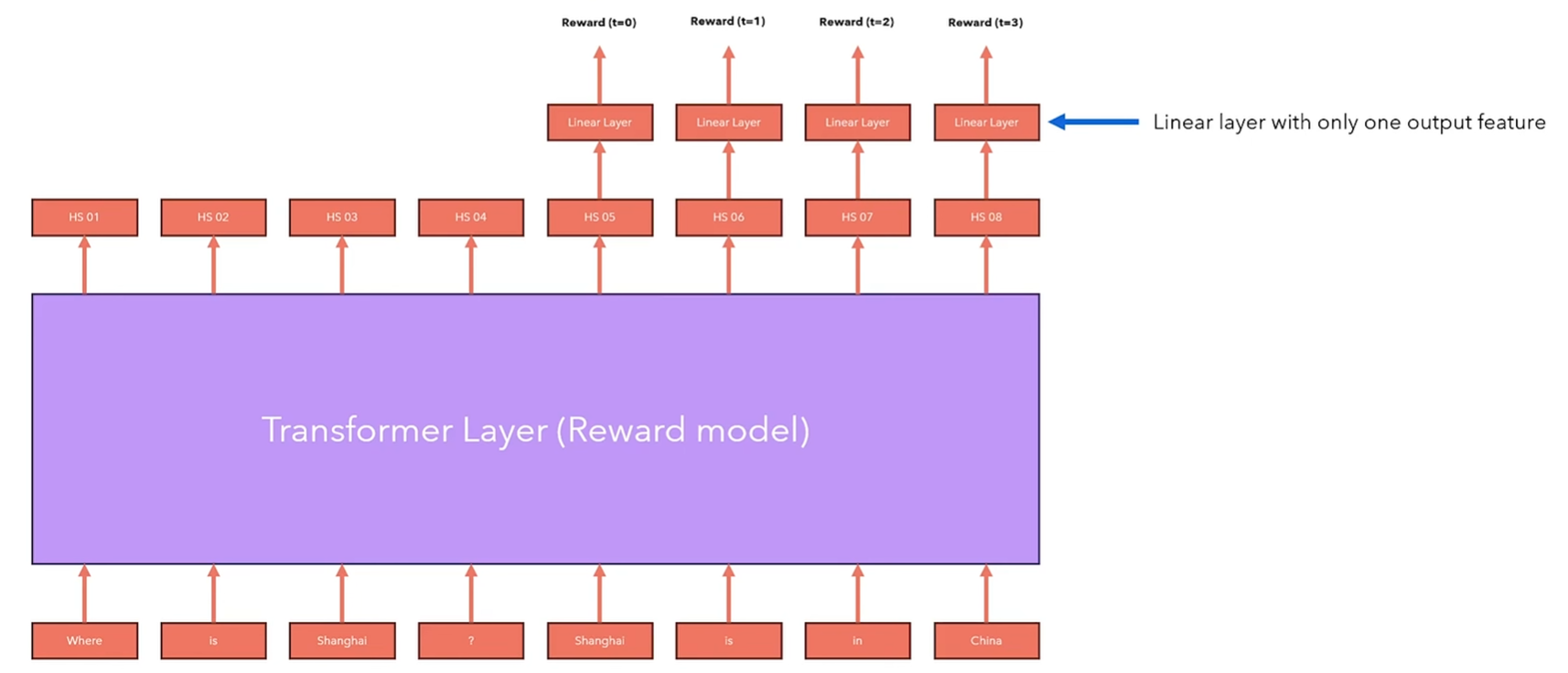
在HuggingFace, 我们可以通过使用RewardTrainer和AutoModelForSequenceClassification训练一个custom reward模型，即拥有一个特殊先行层在顶部的语言模型。

我们只需要要求语言模型输出最后一个token的隐藏层，然后输入进线性层计算奖励，然后根据之前所说的Loss训练模型。

   def compute_loss(
        self,
        model: Union[PreTrainedModel, nn.Module],
        inputs: dict[str, Union[torch.Tensor, Any]],
        return_outputs=False,
        num_items_in_batch=None,
    ) -> Union[torch.Tensor, tuple[torch.Tensor, dict[str, torch.Tensor]]]:
        rewards_chosen = model(
            input_ids=inputs["input_ids_chosen"],
            attention_mask=inputs["attention_mask_chosen"],
            return_dict=True,
        )["logits"]
        rewards_rejected = model(
            input_ids=inputs["input_ids_rejected"],
            attention_mask=inputs["attention_mask_rejected"],
            return_dict=True,
        )["logits"]
        # calculate loss, optionally modulate with margin
        if "margin" in inputs:
            loss = -nn.functional.logsigmoid(rewards_chosen - rewards_rejected - inputs["margin"]).mean()
        else:
            loss = -nn.functional.logsigmoid(rewards_chosen - rewards_rejected).mean()

        if self.args.center_rewards_coefficient is not None:
            loss += self.args.center_rewards_coefficient * torch.mean((rewards_chosen + rewards_rejected) ** 2)

        if return_outputs:
            return loss, {
                "rewards_chosen": rewards_chosen,
                "rewards_rejected": rewards_rejected,
            }
        return loss

3. 策略 Policy

3.1 强化学习中的轨迹

我们之前说过，强化学习的目标是选择一个policy,当agent根据这个策略行动可以最大化返回的期望值。

\[\pi^* = {arg\,max}_\pi J(\pi) \]

策略的期望值，就是所有可能轨迹(trajectories)期望值之和：

\[J(\pi) = \int_\tau\ P(\tau | \pi) R(\tau) = E_{\tau \sim \pi} [R(\tau)] \]

轨迹是从初始state开始的一系列（action, state)：

\[\tau = (s_0,a_0,s_1,a_1, ···) \]

我们把下一个状态视作随机的并进行建模：

\[s_{t+1} \sim P(·|s_t,a_t) \]

因此我们可以用下面的公式定义轨迹·：

\[P(\tau|\pi) = \rho_0(s_0) \prod_{t = 0}^{T - 1} P(s_{t+1}|s_t,a_t)\pi(a_t|s_t) \]

我们通常倾向于使用折扣奖励（因为我们喜欢及时奖励而不是长远奖励）：

\[R(\tau) = \sum_{t = 0}^{\infty}\gamma^tr_t \]

Note: \(0<\gamma < 1\)
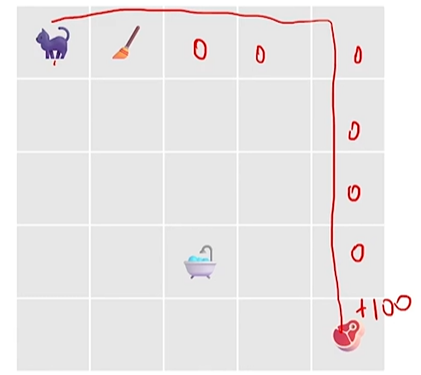
如下如所示，计算的时候应该是 \(R(\tau) = \gamma^{1} * (-1) + 0 +...+ \gamma^{8} * (100) \)

3.2 语言模型下的轨迹

当我们处理的是一个语言模型时，我们希望能微调语言模型使之以获取最大reward的路径选择下一个token：

\[\pi^* = {arg\,max}_\pi J(\pi) \]

轨迹是从一系列prompts(state) 和他们下一个token(action)

\[\tau = (s_0,a_0,s_1,a_1, ···) \]

目标：策略的期望最大
也就是：训练一个policy神经网络\(\pi\),在所有状态S下，给出相应的Action，得到的Return期望最大
也就是：训练一个policy神经网络\(\pi\),在所有的Trajectory中，得到的Return期望最大

3.3 使用策略梯度优化训练一个policy网络

\[J(\pi_\theta) = E_{\tau \sim \pi_\theta} [R(\tau)] \]

当我们提到深度神经网络，我们的目标是迭代地改变神经网络的参数来最小化损失函数的值，这是典型随机梯度下降的用法，但是在我们的案例中，我们希望最大化这函数，因此我们使用随机梯度上升：

\[\theta_{k+1} = \theta_k + \alpha \nabla_\theta {J(\pi_\theta)|}_{\theta_k} \]

策略的梯度叫做 policy gradient, 优化这种策略的算法叫做policy gradient algorithms.

现在的问题就是，如何计算梯度，我们需要考虑所有可能的轨迹，这在计算上是不可行的，因为这是一种computationally intractable问题，除非我们有一个很小的state space。

a. 梯度表达式：

\[\nabla_\theta J(\pi_\theta) = \nabla_\theta \mathbb{E}_{\tau \sim \pi_\theta}[R(\tau)] \]

\(R(\tau)\)：一条轨迹 的总回报。

\(\tau \sim \pi_\theta\)：轨迹是从策略\(\pi_\theta\)中采样得到的。

b. 期望扩展为积分（连续就是积分，离散就是求和）：

\[\nabla_\theta \mathbb{E}_{\tau \sim \pi_\theta} [R(\tau)] = \nabla_\theta \int_\tau P(\tau|\theta) R(\tau) d \tau \]

c. 将梯度移到积分内部（换序积分定理（也称为微分与积分的交换定理））：

\[\int_\tau \nabla_\theta P(\tau|\theta) R(\tau) d \tau \]

d. 引入对数导数技巧（log-derivative trick）：

\[\nabla_\theta P(\tau|\theta) = P(\tau|\theta) \nabla_\theta \log P(\tau|\theta) \]

代入后，得到：

\[\int_\tau P(\tau|\theta) \nabla_\theta \log P(\tau|\theta) R(\tau) d\tau \]

e. 返回期望形式：

\[\mathbb{E}_{\tau \sim \pi_\theta} [ \nabla \theta \log P(\tau|\theta) R(\tau)] \]

f. 分解轨迹的概率：

\[P(\tau|\theta) = \rho_0(s_0) \prod_{t=0}^T \pi_ \theta(a_t|s_t) P(s_{t+1}|s_t, a_t) \]

Note：环境的动态模型（状态转移概率）与策略参数无关，所以对 \(\theta\) 求导只作用在策略上。

如下所示，等式两边同时加上log:

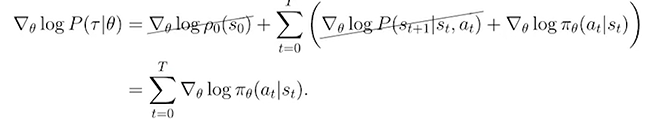
g. 最终公式（策略梯度）：

\[\nabla_\theta J(\pi_\theta) = \mathbb{E}_{\tau \sim \pi_\theta} \left[\sum_{t=0}^T \nabla_\theta \log \pi_\theta(a_t|s_t) R(\tau) \right] \]

\(R(\tau)\)：轨迹的总回报。

\(\log \pi_\theta(a_t|s_t)\)：每个时间步策略的对数概率。

对于这个期望值，我们可以通过对收集到的一组轨迹（也就是一系列行动的记录）进行采样平均来近似这个期望值。

换句话说，我们通过观察和记录多个回合的行动，然后计算这些记录的平均值，来估计这个期望值。

\[\hat{g} = \frac{1}{|D|} \sum_{\tau \in D} \sum_{t=0}^T \nabla_\theta \log \pi_\theta(a_t|s_t) R(\tau) \]

RECAP:截至目前，我们学会了什么？

目标：通过梯度方法优化策略的参数 ，以最大化预期奖励。

算法步骤：

a. 创建策略网络：

使用一个神经网络定义策略\(\pi_\theta\)，输入为当前状态\(s_t\)，输出为在动作空间上的概率分布\(\pi_\theta(a_t|s_t)\)。

b. 采样轨迹：

使用策略\(\pi_\theta\)来与环境交互，生成轨迹（包括状态\(s_t\)、动作\(a_t\)、奖励\(R(\tau)\)）。通常每条轨迹可以运行固定步数（如 100 步）或直到达到终止条件。

c. 计算梯度：

根据公式：

\[\hat{g} = \frac{1}{|D|} \sum_{\tau \in D} \sum_{t=0}^T \nabla_\theta \log \pi_\theta(a_t|s_t) R(\tau) \]

d. 更新策略参数：

使用随机梯度上升更新参数：

\[\theta_{k+1} =\theta_k + \alpha \nabla_\theta J(\pi_\theta)|_{\theta_k} \]

e. 循环迭代：

返回第 b 步，继续采样新的轨迹并重复以上步骤，直到收敛。

4. 为语言模型生成轨迹

还记得我们为reward model建立的偏好数据集吗？我们使用这些问题询问模型以生成回答。然后我们计算生成回答的reward，并根据估计的策略梯度训练模型。

如何计算语言模型的策略log probabilities

计算每个轨迹的reward

4.1 策略梯度优化GPO存在的问题

问题：

梯度估计是无偏的(unbiased)（意思是他可以收敛到真实的梯度），但是它具有很高的方差（varience)

解决：

方法一 : 采用 "rewards to go"（剩余奖励）来替代整条轨迹上的累积奖励

\(R(τ)\)

核心思想：you can't alter the past

a. 原始梯度公式

最初的梯度公式：

\[\nabla_{\theta} J(\pi_\theta) = \mathbb{E}_{\tau \sim \pi_\theta} \left[ \sum_{t=0}^{T} \nabla a_{\theta} \log \pi_\theta(a_t|s_t) R(\tau) \right] \]

• 问题：公式将整个轨迹的累积奖励 $ R(\tau)$与所有时间步的梯度相乘。
• 结果：由于 \(R(\tau)\)包含了从 \(t=0\)到\(T\)的所有奖励，梯度的方差非常高，尤其是在奖励稀疏或延迟时。

---

b. 改进：按时间步分解奖励

将公式重写为：

\[\nabla_{\theta} J(\pi_\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t=0}^{T} \nabla_{\theta} \log \pi_\theta(a_{i,t} | s_{i,t}) \left( \sum_{t=0}^{T} r(s_{i,t}, a_{i,t}) \right) \]

• 每个动作梯度乘以整条轨迹的奖励总和。
• 发现的问题：对于一个具体时间步 ( t )，轨迹中之前的奖励（即 ( t'<t ) 的奖励）对当前动作无关紧要，却仍然被考虑进了公式（因为过去已经无法改变）。

---

c. 引入 “rewards to go”

为了减少方差，使用 "rewards to go" \(\sum_{t'=t}^{T} r(s_{i,t'}, a_{i,t'})\) 来替换原始的轨迹总奖励\(R(\tau)\)。改写后的公式为：

\[\nabla_{\theta} J(\pi_\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t=0}^{T} \nabla_{\theta} \log \pi_\theta(a_{i,t} | s_{i,t}) \left( \sum_{t'=t}^{T} r(s_{i,t'}, a_{i,t'}) \right) \]

• 解释：
  • 对于每个时间步 $ t$，只计算从当前时间步到轨迹结束的累积奖励。
  • 忽略过去的奖励，因为它们在期望中会相互抵消，不影响最终梯度的无偏性。

---

d. 减少方差的原因

• 原始公式中，过去的奖励\(t' < t\)对当前动作梯度没有直接影响，但由于被包含进公式中，会引入额外的噪声（方差）。
• 改用 "rewards to go" 后，公式更准确地反映了当前动作对未来奖励的直接影响，从而降低了梯度估计的方差。

方法二：引入基准函数（Baseline）来进一步减少梯度估计方差。

• 目标：通过引入基准函数\(b\)，减少梯度估计的方差，改善优化过程的稳定性。
• 常用基准：状态价值函数 \(V^\pi(s)\)，也可以使用其他函数，具体取决于任务和模型的设计。
• 优势：减小了无关噪声的影响，让策略更专注于改进未来表现。

a. 梯度公式中的基准函数

基础的梯度公式为：

\[\nabla_{\theta} J(\pi_\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t=0}^{T} \nabla_{\theta} \log \pi_\theta(a_{i,t} | s_{i,t}) \left( \sum_{t'=t}^{T} r(s_{i,t'}, a_{i,t'}) \right) \]

通过引入一个基准函数 (b)（Baseline），公式变为：

\[\nabla_{\theta} J(\pi_\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t=0}^{T} \nabla_{\theta} \log \pi_\theta(a_{i,t} | s_{i,t}) \left( \sum_{t'=t}^{T} r(s_{i,t'}, a_{i,t'}) - b \right) \]

b. 为什么引入基准函数？

1. 无偏性：可以证明，减去一个基准函数\(b\)并不会改变梯度估计的无偏性。
   • 也就是说，基准函数的引入不会对梯度的方向或期望值产生影响。
2. 减少方差：引入基准函数后，公式中引入了一种对奖励的“校正”，从而有效减少了梯度估计中的方差。

c. 选择基准函数的方式

常用的基准函数是状态价值函数\(V^\pi(s)\)：

\[V^\pi(s) = \mathbb{E}_\pi \left[ \sum_{t'=t}^{T} r(s_{t'}, a_{t'}) \, | \, s_t = s \right] \]

• 解释：
  • \(V^\pi(s)\)表示从当前状态\(s_t\)出发，按照策略 \(\pi\)所能获得的期望未来奖励。
  • 使用 \(V^\pi(s)\)作为基准，可以有效去掉与当前状态 \(s_t\)无关的波动。

例子：高值状态与低值状态

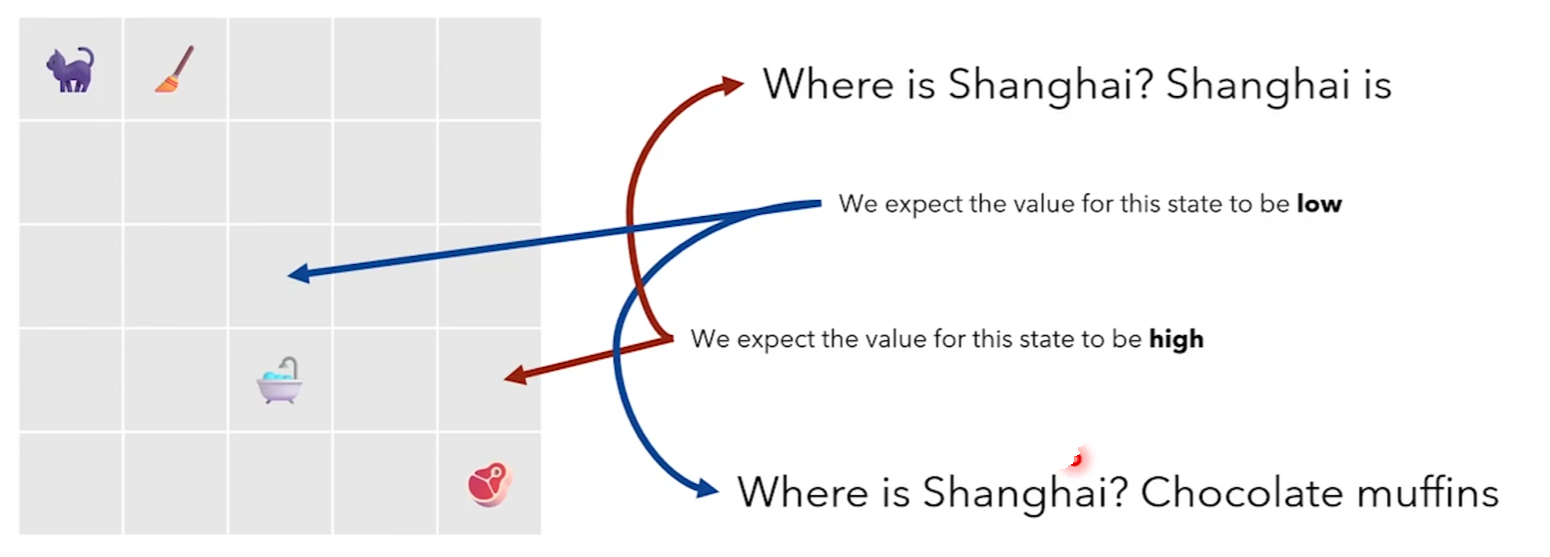
• 对于某个状态 \(s_t\)，如果期望的未来奖励（价值）较低，基准值会相应较低。
• 如果某个状态的未来奖励较高（即更接近目标或有利），基准值会较高。
• 减去基准值后，梯度更新会更聚焦于当前动作的实际贡献，而不是受环境噪声或总体奖励波动的影响。

估计\(V^\pi (s)\):

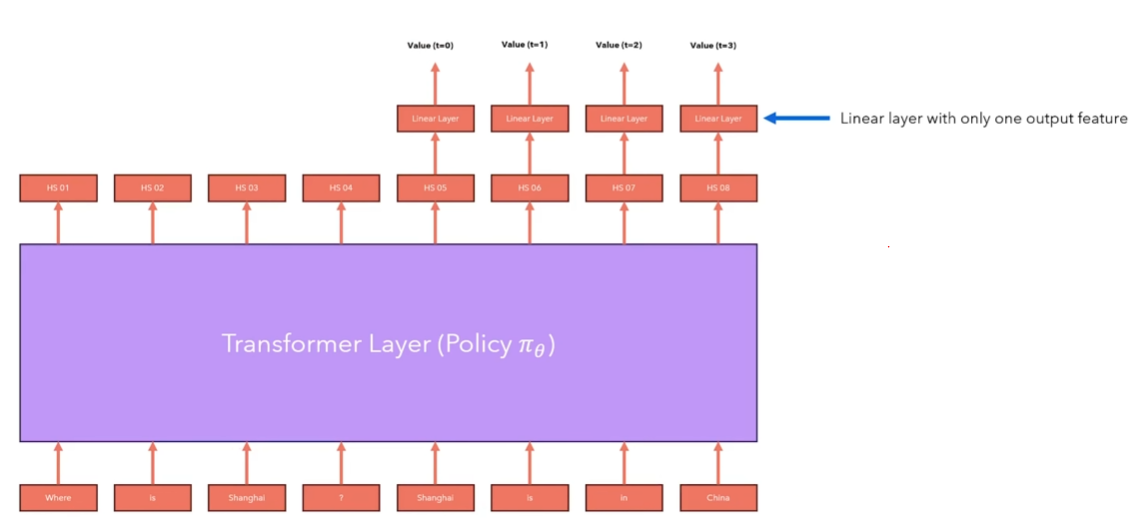
注意：语言模型已经有一个线性层（把隐藏层转化为logits值）这里添加的是另一个线性层。

d. 具体优化效果

• 引入基准函数后：
  • 当 \(\sum_{t'=t}^{T} r(s_{i,t'}, a_{i,t'})\) 大于基准值 \(b\)时，表示当前动作比预期更好，梯度更新会倾向于强化该动作。
  • 当 \(\sum_{t'=t}^{T} r(s_{i,t'}, a_{i,t'})\)小于基准值 \(b\)时，表示当前动作比预期更差，梯度更新会倾向于削弱该动作。

e. 引入 Q 和 V：

(未完待续)