leetcode 每日一题 gcd+枚举

1819. 序列中不同最大公约数的数目

给你一个由正整数组成的数组 nums 。
数字序列的 最大公约数 定义为序列中所有整数的共有约数中的最大整数。
  例如，序列 [4,6,16] 的最大公约数是 2 。
  数组的一个子序列本质是一个序列，可以通过删除数组中的某些元素（或者不删除）得到。
例如，[2,5,10] 是 [1,2,1,2,4,1,5,10] 的一个子序列。
计算并返回 nums 的所有 非空 子序列中 不同 最大公约数的 数目 。
 
 来源：力扣（LeetCode）
 链接：https://leetcode.cn/problems/number-of-different-subsequences-gcds
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

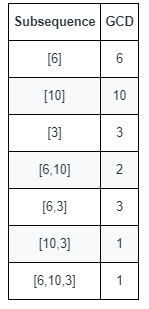
输入：nums = [6,10,3]
输出：5
解释：上图显示了所有的非空子序列与各自的最大公约数。
不同的最大公约数为 6 、10 、3 、2 和 1 。

 本题最初的想法时对所有子序列求最大公因数，并对最大公因数的个数进行统计。
 但是在实际操作过程中，截取所有子序列的部分就极为复杂，到这儿就不会做了，在查看题解后，题解给出了一种新的思路：

既然遍历所有的子序列过于复杂，那为什么不直接遍历所有可能的最大公因数取值呢？因为序列[a1,a2,,,,,,,,max]的所有最大公因数必然在1~max之间，所以直接对1到max中的数的倍数进行判别，查看其倍数的最大公因数是否为对应数即可。

class Solution {
    public int gcd(int x,int y)
    {
        int mid;
        while(x!=0)
        {
            mid=x;
            x=y%x;
            y=mid;
        }
        return y;
    }
    public int countDifferentSubsequenceGCDs(int[] nums) {
        int ans=0,max=0;
        for(int x: nums) max=Math.max(x,max);
        var has= new boolean[max+1];
         for(int x:nums) has[x]=true;
        for(int i=1;i<=max;i++) //所有的最大公因数的可能就是 1----max
        {
            int g=0;//0与任何数的最大公因数等于该数本身
            for(int j=i;j<=max;j=j+i) // 遍历所有 i的倍数
            {
                if(has[j])//存在i的倍数，则求这些倍数的最大共因数是否为i
                {
                    g=gcd(g,j);
                }
            }
            if(g==i) ans++;
        }
    return ans;
    }
}