贪心

一般贪心

这类题型可以直接看出贪心思路，只需要某一个条件最大即可，排序取值即可

推公式排序

保护花
这个题就不是由某一元素决定的，则需要推一下公式
（公式推导来自牛客dalao）
贪心策略
这个贪心策略很简单：假设我们现在有两头相邻搬运的牛。这两头牛交换顺序对答案可能有影响，但是对其他牛没有影响，所以贪心成立。
然后我们就假设两头牛分别在前面的情况，用来判断那种情况好（这里我们假设为A牛和B牛，sum表示在这两头牛之前花的时间）：
如果先把A搬回去就有：sum * A.dedtroy + (sum + 2 * A.time) * B.destroy。
那如果先搬掉B呢就有：sum * B.destroy + (sum + 2 * B.time) * A.destroy。
那现在我们两种情况有了，我们接下来不妨设：A在前比B在前要更好！就可以得到方程：
sum * A.dedtroy + (sum + 2 * A.time) * B.destroy < sum * B.destroy + (sum + 2 * B.time) * A.destroy。
化简之后就是：A.time * B.destroy < B.time * A.destroy。就是说只要满足这个，A就可以放在B的前面，反之亦然。

由这一推导思路可知，我们排序顺序由两个元素乘积决定

糖果传递

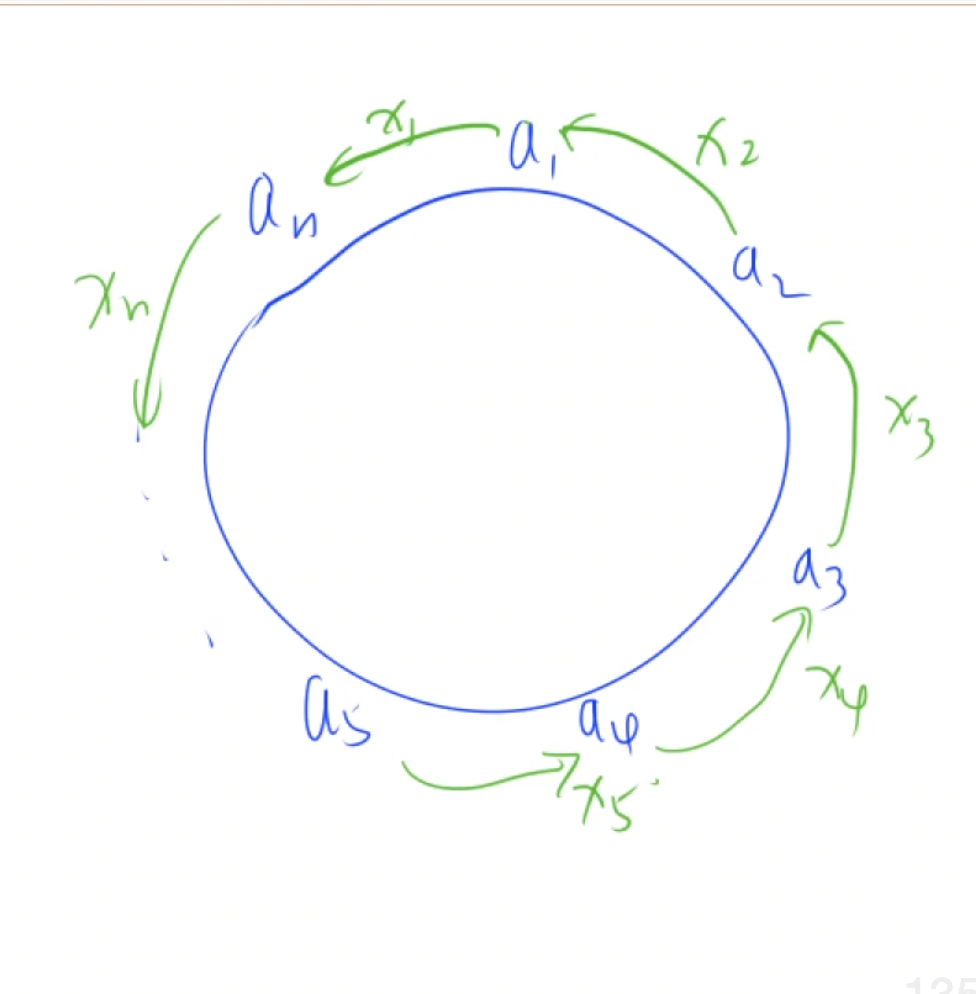
这个题也需要进行公式推导，因为每个小朋友只能把糖果分给相邻两个人，可以得到基础方程组

\[\begin{cases}a_1-x_1+x_2=\overline{a}\\a_2-x_2+x_3=\overline{a}\\......\\a_n+x_1-x_n=\overline{a}\\\end{cases} \]

化简可得

\[ \begin{cases}x_1-x_2=a_1-\overline{a}\\x_2-x_3=a_2-\overline{a}\\......\\x_n-x_1=a_n-\overline{a}\end{cases} \]

将\(x_1\)记为未知数，可以解出其它值为

\[\begin{cases} x_n=x_1-(\overline{a}-a_n)\\ x_{n-1}=x_1-(2\overline{a}-a_n-a_{n-1})\\ ......\\ x_2=x1-((n-1)\overline{a}-a_n-...-a_2)\\ x_1=x_1 \end{cases} \]

这题就转化为货仓选址找到\(x_1\)的位置到其它各处的位置最短，转化为贪心问题

区间贪心

雷达设备
这道题可以转化为从小岛为圆心画圆，这样就转化为区间取点问题，右端点排序，尽可能少的取点