树
二叉树
遍历方式
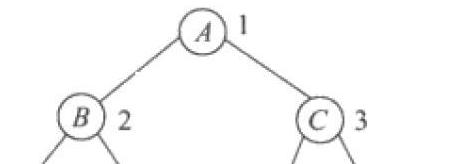
前序遍历: 根节点在前面,即根左右 上图结果为ABC
中序遍历: 根节点在中间,即左根右 上图结果为BAC
后序遍历: 根节点在后面,即左右根 上图结果为BCA
层序遍历:一层一层遍历 上图结果为ABC
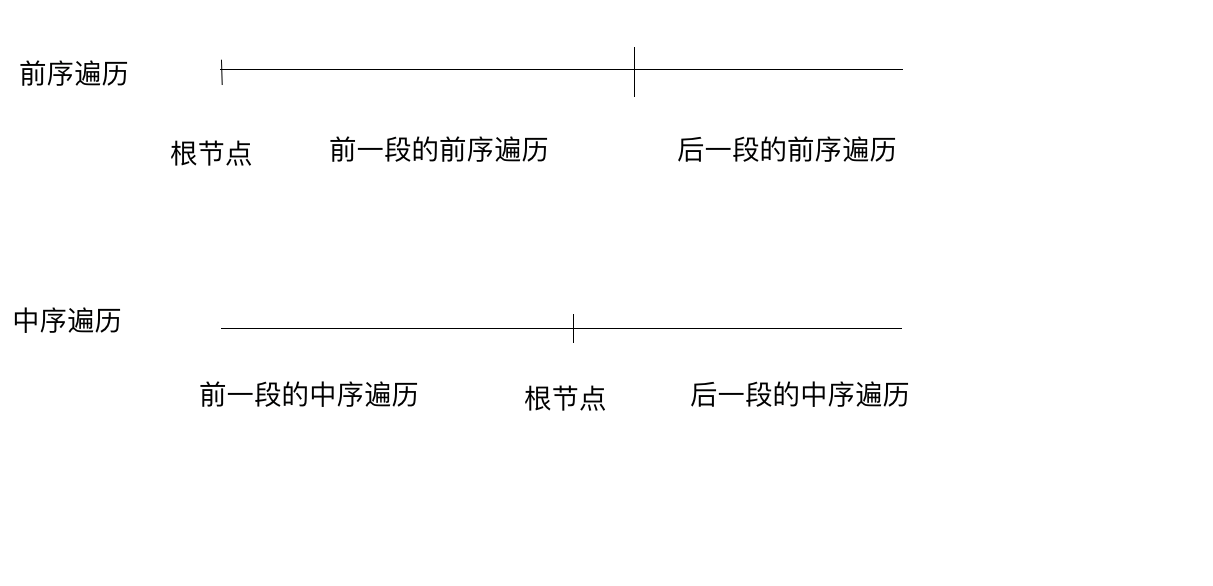
前中后序遍历
此类题型就是提供中序遍历以及前序遍历和后序遍历中的一种,得到另外一种
例如提供前序遍历和中序遍历
每次递归查找此时的根节点并输出
void dfs(string pre,string in){
if(pre.empty()) return;
char c=pre[0];
int k=in.find(c);
dfs(pre.substr(1,k),in.substr(0,k));
dfs(pre.substr(k+1),in.substr(k+1));
cout<<c;
}
输出c的位置要注意,前序和后序不相同
层序遍历
提供层序遍历的结果,输出第k层的内容
long long i,n,k,f=0,d ;
cin>>n;
for(i=1;i<=n;i++){
cin>>a[i];
}
cin>>k;
d=power(2,k);
for(i=d;i<=min(n,d*2);i++)
{
cout<<a[i]<<" ";
f=1;
}
if(f==0){
cout<<"EMPTY"<<endl;
}
return 0;
power函数可以用快速幂优化
特殊二叉树
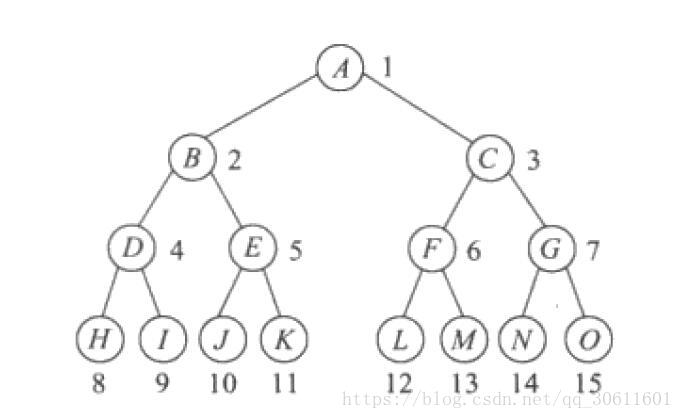
满二叉树
k层树共有\(2^{k-1}\)个节点,
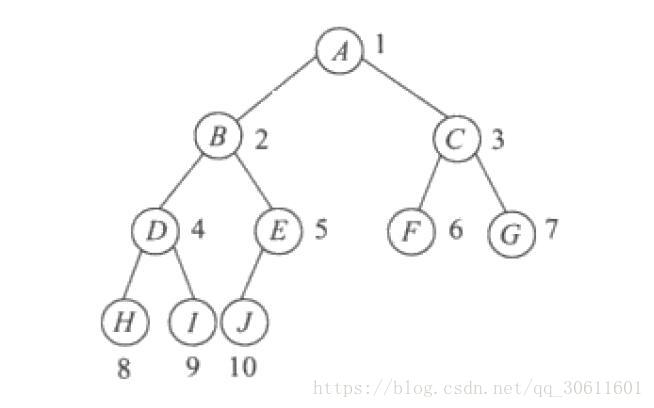
完全二叉树
从1-n个节点就是满二叉树中的1-n的节点
二叉搜索树
根节点一定大于左子树的值,一定小于右子树的值
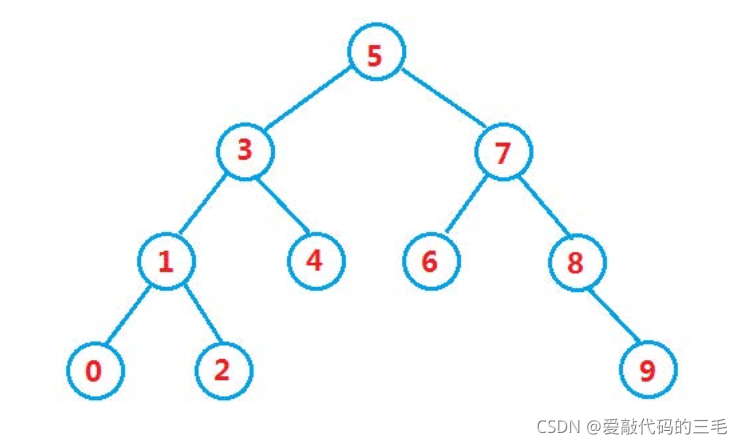
树的遍历
先用vector存树的每一条边(单向只存一次)
for(int i=1,x,y;i<=n-1;i++){
//int x,y;
cin>>x>>y;
e[x].push_back(y);
e[y].push_back(y);
}
再用dfs查找每一条边
void dfs(int x){
for(auto i:e[x]) {
if (f[i])
continue;
f[i]=1;
dep[i]=dep[x]+1;
dfs(i);
}
}
树与二分图
所有的树都可以转化为二分图
二分图概念
顶点集V可分割为两个互不相交的子集,并且图中每条边依附的两个顶点都分属于这两个互不相交的子集,两个子集内的顶点不相邻。
树与二分图转化
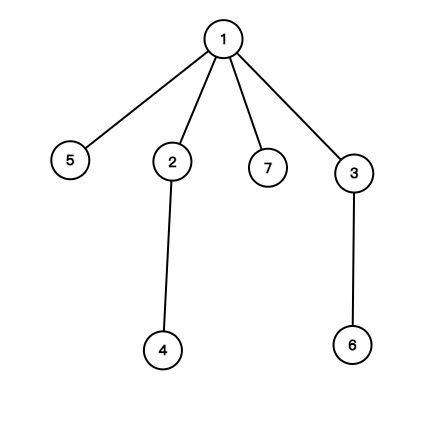
.png)
由图中可知,树转化为二分图就是将树的奇数层和偶数层分开,所以要将树的每个点的深度存一下(树的遍历)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号