java题目集1-3的总结
前言
在pta题目集1-3中,题目集一的题量较另外两个比较多,但是难度低,考察的是Java的一些基本语法语句(选择语句)和实用数据的使用,根据之前学C面向过程的知识储量基本上能够完成该题目集,做题时主要注意java的double类型数据使用时的精度(第二、八题)和计算时存在误差(第七题),需要格外注意输出格式和计算等值时的误差分析。
题目集二的题量只有三题,难度适中,主要考察的是Java的String格式类型的使用、判断与转换,根据之前使用String的相关知识还是能够完成,其中第二题的串口字符解析题需要理解题目意思并查询相关资料了解奇偶效验位的定义,最后成功地完成题目集。
题目集三的题量也只有三题,但难度却感觉与前两个题目集相比,难度直接成几何倍数增长,并且其中的题目基本上是一题连接着一题的知识点,环环相扣,考察的是字符串,double类型数据计算,面向对象等的相关知识,对于初学Java的我感觉非常具有挑战,做题目前翻阅java课本以及在csdn网站上寻找其中相关数据格式、语法知识的使用,再进行不断地尝试编写代码和编译运行,但第三个题目的30个测试点选项五的两个测试点始终无法通过,测试样例通过但是测试点未通过。
设计与分析
题目集一:
7-7 判断三角形类型(10分)
输入三角形三条边,判断该三角形为什么类型的三角形。
输入格式:
在一行中输入三角形的三条边的值(实型数),可以用一个或多个空格或回车分隔,其中三条边的取值范围均为[1,200]。
输出格式:
(1)如果输入数据非法,则输出“Wrong Format”;
(2)如果输入数据合法,但三条边不能构成三角形,则输出“Not a triangle”;
(3)如果输入数据合法且能够成等边三角形,则输出“Equilateral triangle”;
(3)如果输入数据合法且能够成等腰直角三角形,则输出“Isosceles right-angled triangle”;
(5)如果输入数据合法且能够成等腰三角形,则输出“Isosceles triangle”;
(6)如果输入数据合法且能够成直角三角形,则输出“Right-angled triangle”;
(7)如果输入数据合法且能够成一般三角形,则输出“General triangle”。

度量分析:
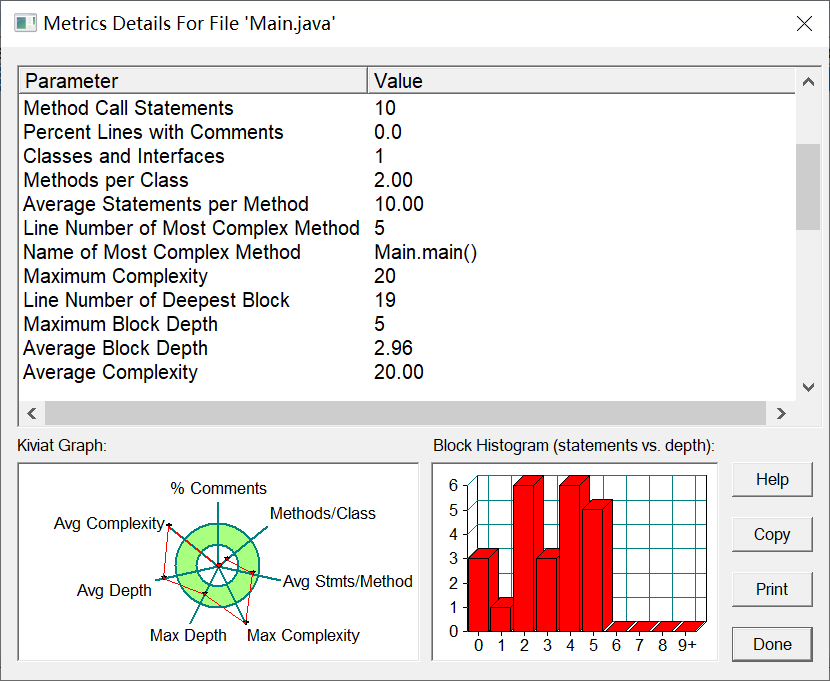
这题比较简单,整体的思路和题目含义清晰,不需要使用面向对象创建多个类去完成,只需要Main类就能实功能,先判定出正确格式,然后不断使用if-else语句不断判断筛选,得出相应的输出。
主要代码分析:
if(a<1||a>200||b<1||b>200||c<1||c>200){ System.out.println("Wrong Format"); } else{ if((a+b)<=c||(a+c)<=b||(b+c)<=a){ System.out.println("Not a triangle"); } else{ if(a==b&&a==c&&b==c){ System.out.println("Equilateral triangle"); } else if((a==b&&Math.abs(c*c-a*a-b*b)<0.00001)||(a==c&&Math.abs(b*b-a*a-c*c)<0.00001)||(c==b&&Math.abs(a*a-c*c-b*b)<0.00001)){ System.out.println("Isosceles right-angled triangle"); } else if(a==b||a==c||b==c){ System.out.println("Isosceles triangle"); } else if(a*a==b*b+c*c||b*b==a*a+c*c||c*c==a*a+b*b){ System.out.println("Right-angled triangle"); } else{ System.out.println("General triangle"); } } }
代码思路:使用if-else语句,先判断该三角形输入的数据是否合法(1-200),合法的话再判断是否能构成三角形(两边之和大于第三边的定理),如果能构成三角形,再判断是等边三角形或者等腰直角三角形或者等腰三角形或者直角三角形或者一般三角形,其中判断等腰直角三角形的时候,double类型数据计算时会丢失部分精度,所以需要算上误差,并使用了Math.abs函数算成绝对值进行比较,得出是否为等腰直角三角形的判断结果。
优缺点:
优点:1.整体if-else语句的判断条件比较清晰,便于理解,并且可操作性强。
2.能够考虑到直角三角形的边长可能存在无理数,会产生误差,影响精度,故使用Math.abs(c*c-a*a-b*b)<0.00001,让判断结果更精确。
缺点:1.if-else语句的使用过多,导致代码繁杂。
2.判定是否为直角三角形时未测试其计算精度,导致判断结果有误差,一些无理数边长数据被省略。
3.等腰直角三角形和等腰三角形、直角三角形的部分条件重合,但只能输出一个三角形类型,输出不严谨且这三个三角形类型的输出顺序不能确认,使得部分输出样例有偏差。
题目集二:
7-2 串口字符解析 (40 分)
RS232是串口常用的通信协议,在异步通信模式下,串口可以一次发送5~8位数据,收发双方之间没有数据发送时线路维持高电平,相当于接收方持续收到数据“1”(称为空闲位),发送方有数据发送时,会在有效数据(5~8位,具体位数由通信双方提前设置)前加上1位起始位“0”,在有效数据之后加上1位可选的奇偶校验位和1位结束位“1”。请编写程序,模拟串口接收处理程序,注:假定有效数据是8位,奇偶校验位采用奇校验。
输入格式:
由0、1组成的二进制数据流。例如:11110111010111111001001101111111011111111101111
输出格式:
过滤掉空闲、起始、结束以及奇偶校验位之后的数据,数据之前加上序号和英文冒号。
如有多个数据,每个数据单独一行显示。
若数据不足11位或者输入数据全1没有起始位,则输出"null data",
若某个数据的结束符不为1,则输出“validate error”。
若某个数据奇偶校验错误,则输出“parity check error”。
若数据结束符和奇偶校验均不合格,输出“validate error”。
如:11011或11111111111111111。
例如:
1:11101011
2:01001101
3:validate error

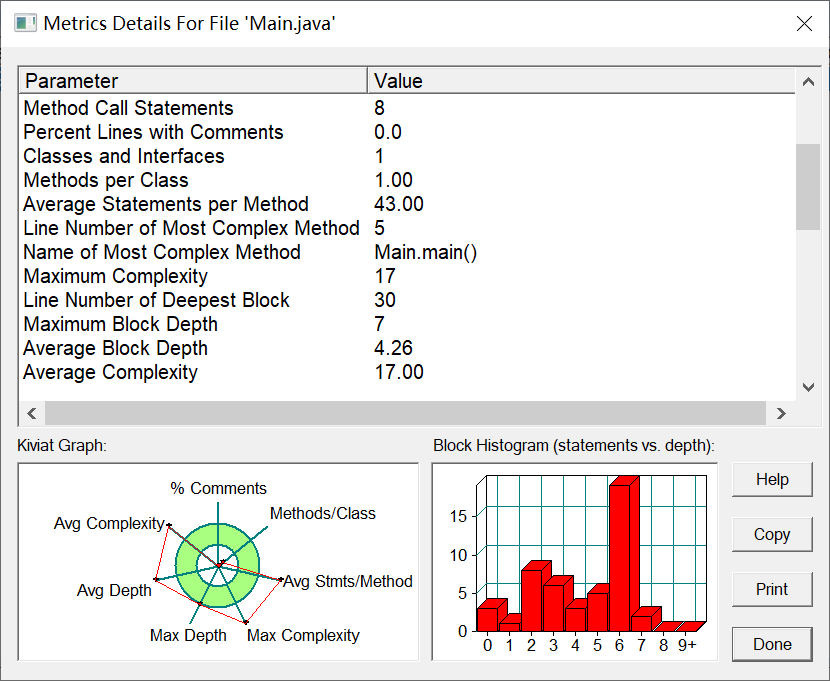
该题目是对串口字符解析,整体题目结构不复杂,故也不需要创建多个类进行解答,只需使用Main类。首先得对该题目进行详细的分析,经过查询相关奇偶效验性的含义,明白奇偶效验是判断“1”的个数为奇数还是偶数,并是采用的是奇效验,判定的数据段为有效数据和其后一位计算判定,再运用for循环语句,if-else语句,变量标识符,解答该题目。
主要代码分析:
if(b.length<11){ x=1; } else{ String c="1"; for(int i=1;i<b.length;i++){ c=c+1; } if(c.equals(a)){ x=1; } } if(x==1){ System.out.println("null data"); } else{ for(int k=0;k<b.length;k++){ if(b[k]=='0'){ for(int j=k+1;j<=k+9;j++){ if(b[j]=='1'){ z=z+1; } } if(b[k+10]!='1'){ System.out.println(y+":"+"validate error"); y++; k=k+10; z=0; continue; } else if(z%2==0){ System.out.println(y+":"+"parity check error"); y++; k=k+10; z=0; continue; } else if(b[k+10]!='1'&&z%2==0){ System.out.println(y+":"+"validate error"); y++; k=k+10; z=0; continue; } else{ System.out.print(y+":"); for(int t=k+1;t<k+9;t++){ System.out.print(b[t]); } System.out.println(); y++; k=k+10; z=0; continue; } } } }
代码思路:先用if-else语句和for语句以x为标识符,判断输入数据格式是否错误,如果正确再用for语句对输入的字符串进行解析,利用z来计算“1”的个数进行奇偶效验,每次输出一个结果后,y+1来表示下一结果的顺序,k+10来略过解析完的字符串段,使用continue保证进行下一次的循环,最后对每段字符的判断若某个数据的结束符不为1,则输出“validate error”。若某个数据奇偶校验错误,则输出“parity check error”。若数据结束符和奇偶校验均不合格,输出“validate error”。得出相应的结果。
优缺点:
优点:1.for语句循环中,使用了continue,保证了下一次循环的进行。
2.能够较为精准的对字符串解析,并依照题意得出对应结果。
缺点:1.if-else语句与前面题目集7-7一样依旧使用过多,造成程序繁杂。
2.标识符多,并且使用嵌套循环,不易于阅读者理解。
题目集三:
7-1 点线形系列1-计算两点之间的距离 (10 分)
输入连个点的坐标,计算两点之间的距离
输入格式:
4个double类型的实数,两个点的x,y坐标,依次是x1、y1、x2、y2,两个点的坐标之间以空格分隔,每个点的x,y坐标以英文“,”分隔。例如:0,0 1,1或0.1,-0.3 +3.5,15.6。
若输入格式非法,输出"Wrong Format"。
若输入格式合法但坐标点的数量超过两个,输出“wrong number of points”。
输出格式:
计算所得的两点之间的距离。例如:1.4142135623730951
度量分析:
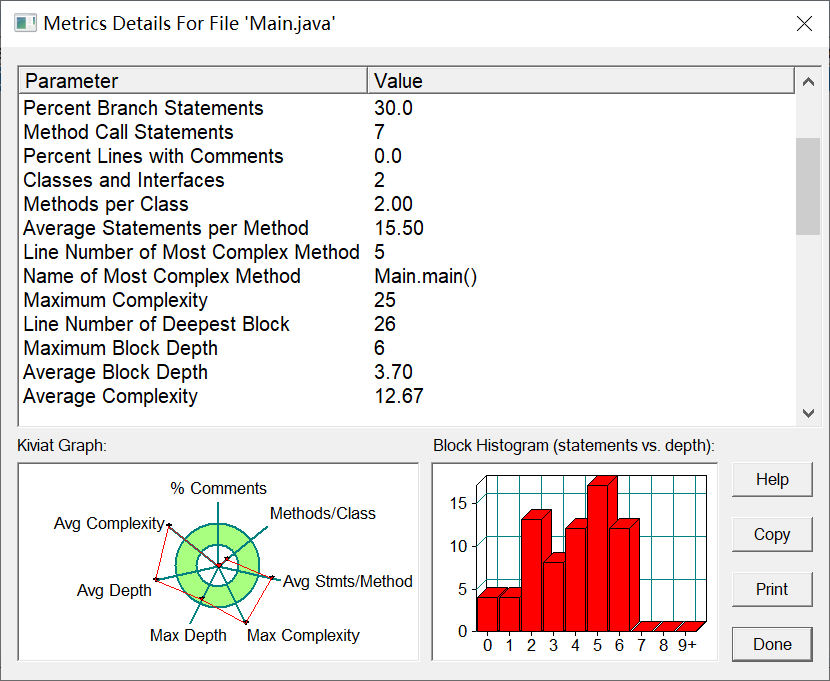
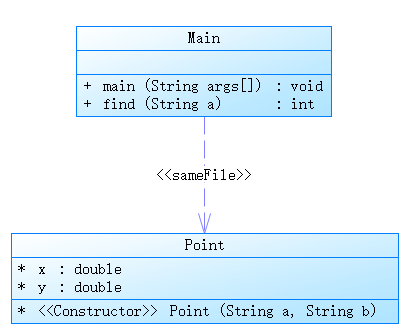
该题目整体思路清晰,只需创建一个Point类(点),主要注意的地方是判断输入格式非法的地方要严谨准确(讨论多种情况),创建一个find方法来判断输入格式,使用新学习的split方法进行分割字符串,il-else语句等,判断输入格式合法且没超过2个点后输出距离。
主要代码分析:
public static int find(String a){ char b[]=a.toCharArray(); for(int i=0;i<b.length;i++){ if(i<=b.length-2) { if((b[i]=='-'||b[i]=='+'||b[i]=='.')&&(b[i+1]=='-'||b[i+1]=='+'||b[i+1]=='.')){ return 1; } } if(b[i]!='.'&&b[i]!='-'&&b[i]!='+'&&(b[i]<'0'||b[i]>'9')){ return 1; } if(b[i]=='0'&&b[i+1]!='.'){ return 1; } } if(b[b.length-1]=='.'||b[0]=='.'){ return 1; } return 0; }
代码思路:此为find方法,返回值为int类型,用以判断输入数据的合法性。将输入的字符串a转换成为字符数组b,判断数组中除了. - + 0-9外是否还有其它非法字符,如果有返回1,并判断. - + 0-9的顺序是否有问题,如果有返回1,这些情况都没有出现,则返回0。
优缺点:
优点:1.if-else语句条件简明,且运用了新学习的tochararray方法和split方法。
缺点:1.使用了许多if-else语句和嵌套循环,代码繁杂过多,,不简洁,不易于理解。
2.测试点测试非法格式有许多种情况未考虑到,仅考虑了部分非法格式,不够完善。
3.未能使用正则表达式,程序过长。
题目集三:
7-2 点线形系列2-线的计算 (42 分)
用户输入一组选项和数据,进行与直线有关的计算。选项包括:
1:输入两点坐标,计算斜率,若线条垂直于X轴,输出"Slope does not exist"。
2:输入三个点坐标,输出第一个点与另外两点连线的垂直距离。
3:输入三个点坐标,判断三个点是否在一条线上,输出true或者false。
4:输入四个点坐标,判断前两个点所构成的直线与后两点构成的直线是否平行,输出true或者false.
5:输入四个点坐标,计算输出前两个点所构成的直线与后两点构成的直线的交点坐标,x、y坐标之间以英文分隔",",并输出交叉点是否在两条线段之内(不含四个端点)的判断结果(true/false),判断结果与坐标之间以一个英文空格分隔。若两条线平行,没有交叉点,则输出"is parallel lines,have no intersection point"。
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。
例如:1:0,0 1,1
如果不符合基本格式,输出"Wrong Format"。
如果符合基本格式,但输入点的数量不符合要求,输出"wrong number of points"。
不论哪个选项,如果格式、点数量都符合要求,但构成任一条线的两个点坐标重合,输出"points coincide",
输出格式:
见题目描述。

度量分析:
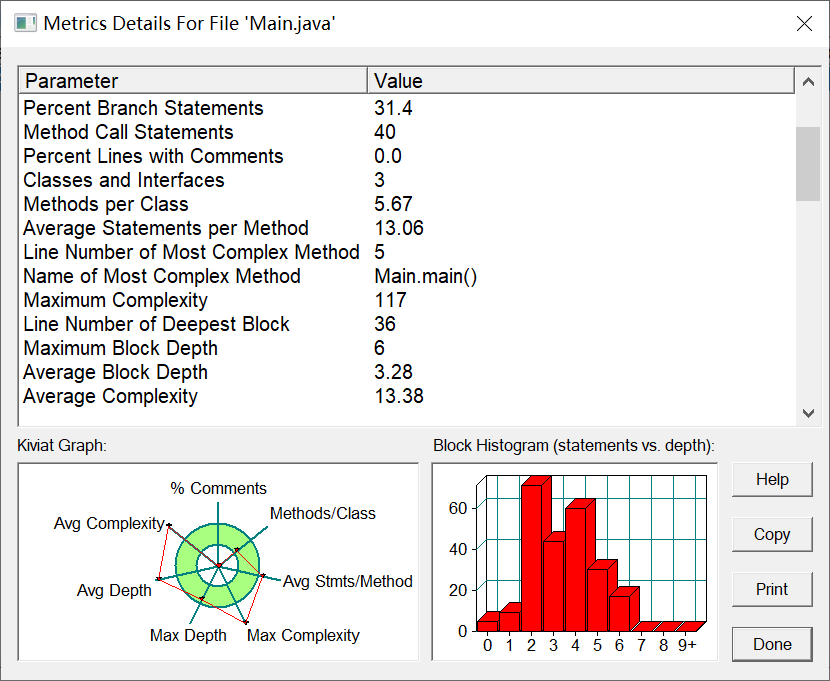
该题目跟题目集三7-1的输入格式判断非法类似,但是因为7-1我的代码判断不是很完善,所以套入这题出现bug有两个测试点未通过,经过完善find方法得以通过,并且我对输入数据的长度和字符数量进行了判断。该题我创建了Point类(点)和Test类(方法),Point类用于取用其中的方法对应题目的选项。通过Main类,Point类,Test类共同完成该题。
主要代码分析:
public static int find(String a){ char b[]=a.toCharArray(); if(b[0]=='0'&&b.length>1){ if(b[1]!='.'){ return 1; } } if(b[0]=='+'||b[0]=='-'){ if(b[1]=='0'&&b.length>2){ if(b[2]!='.'){ return 1; } } if(b[1]<'0'||b[1]>'9'){ return 1; } } for(int k6=0;k6<b.length;k6++){ if(b[k6]==' '||b[k6]==':'){ return 1; } } if(b[b.length-1]=='.'||b[0]=='.'||b[b.length-1]=='+'||b[b.length-1]=='-'){ return 1; } return 0; } public void test1(String a[]){ String a1[]=a[0].split(","); String a2[]=a[1].split(","); Point aa=new Point(a1[0],a1[1]); Point b=new Point(a2[0],a2[1]); if(aa.x==b.x&&aa.y==b.y){ System.out.println("points coincide"); } else{ double s=0; s=(aa.y-b.y)/(aa.x-b.x); if(aa.x==b.x){ System.out.println("Slope does not exist"); } else{ System.out.println(s); } } } public void test2(String a[]){ String a1[]=a[0].split(","); String a2[]=a[1].split(","); String a3[]=a[2].split(","); Point aa=new Point(a1[0],a1[1]); Point b=new Point(a2[0],a2[1]); Point c=new Point(a3[0],a3[1]); if((b.x==c.x&&b.y==c.y)||(aa.x==b.x&&aa.y==b.y)||(aa.x==c.x&&aa.y==c.y)){ System.out.println("points coincide"); } else{ if(b.x==c.x){ System.out.println(Math.abs(aa.x-b.x)); } else if(b.y==c.y){ System.out.println(Math.abs(aa.y-b.y)); } else{ double k=(b.y-c.y)/(b.x-c.x); double b1=b.y-k*b.x; double s=Math.abs(k*aa.x-aa.y+b1)/Math.sqrt(k*k+1); System.out.println(s); } } } public void test3(String a[]){ String a1[]=a[0].split(","); String a2[]=a[1].split(","); String a3[]=a[2].split(","); Point aa=new Point(a1[0],a1[1]); Point b=new Point(a2[0],a2[1]); Point c=new Point(a3[0],a3[1]); if((aa.x==b.x&&aa.y==b.y)||(aa.x==c.x&&aa.y==c.y)||(b.x==c.x&&b.y==c.y)) { System.out.println("points coincide"); } else { if(aa.x==b.x&&b.x==c.x&&aa.x==c.x) { System.out.println("true"); } else if((aa.y-b.y)/(aa.x-b.x)==(aa.y-c.y)/(aa.x-c.x)&&(aa.y-b.y)/(aa.x-b.x)==(b.y-c.y)/(b.x-c.x)&&(b.y-c.y)/(b.x-c.x)==(aa.y-c.y)/(aa.x-c.x)) { System.out.println("true"); } else { System.out.println("false"); } } } public void test4(String a[]){ String a1[]=a[0].split(","); String a2[]=a[1].split(","); String a3[]=a[2].split(","); String a4[]=a[3].split(","); Point aa=new Point(a1[0],a1[1]); Point b=new Point(a2[0],a2[1]); Point c=new Point(a3[0],a3[1]); Point d=new Point(a4[0],a4[1]); if((aa.x==b.x&&aa.y==b.y)||(c.x==d.x&&c.y==d.y)) { System.out.println("points coincide"); } else { if((aa.x==b.x&&c.x==d.x)||(aa.x==b.x&&b.x==c.x&&c.x==d.x)) { System.out.println("true"); } else if((aa.y-b.y)/(aa.x-b.x)==(c.y-d.y)/(c.x-d.x)) { System.out.println("true"); } else { System.out.println("false"); } } } public void test5(String a[]){ String a1[]=a[0].split(","); String a2[]=a[1].split(","); String a3[]=a[2].split(","); String a4[]=a[3].split(","); Point aa=new Point(a1[0],a1[1]); Point b=new Point(a2[0],a2[1]); Point c=new Point(a3[0],a3[1]); Point d=new Point(a4[0],a4[1]); if((aa.x==b.x&&aa.y==b.y)||(c.x==d.x&&c.y==d.y)) { System.out.println("points coincide"); } else { if((aa.x==b.x&&c.x==d.x)||(aa.x==b.x&&b.x==c.x&&c.x==d.x)||(aa.y-b.y)/(aa.x-b.x)==(c.y-d.y)/(c.x-d.x)) { System.out.println("is parallel lines,have no intersection point"); } else { double aa1,aa2,bb1,bb2,c1,c2,m,x,y; aa1=b.y-aa.y; aa2=d.y-c.y; bb1=b.x-aa.x; bb2=d.x-c.x; c1=bb1*aa.y-aa1*aa.x; c2=bb2*c.y-aa2*c.x; m=aa1*bb2-aa2*bb1; x=(bb1*c2-bb2*c1)/m; y=(aa1*c2-aa2*c1)/m; double max1=Math.max(aa.x,b.x); double min1=Math.min(aa.x,b.x); double max2=Math.max(aa.y,b.y); double min2=Math.min(aa.y,b.y); double max3=Math.max(c.x,d.x); double min3=Math.min(c.x,d.x); double max4=Math.max(c.y,d.y); double min4=Math.min(c.y,d.y); if ((x>min1&&x<max1&&y>min2&&y<max2)||(x>min3&&x<max3&&y>min4&&y<max4)) { System.out.println(x+","+y+" true"); } else { System.out.println(x+","+y+" false"); } } } }
代码思路:
第一个是find方法,较7-1进行了完善,对一些我本以为已经排除的字符进行再次判断,并按照输入数据顺序判断字符顺序,最后成功通过遗漏的测试点。
test1方法,void型,用于对应选项一,要特别区分斜率存在和斜率不存在的情况得出相应结果。
test2方法,void型,用于对应选项二,跟test1注意的点一样。
test3方法,void型,用于对应选项三,三个点x坐标相同则true,斜率相同也输出true,其他情况则输出false。
test4方法,void型,用于对应选项四,跟test3的原理类似。
test5方法,void型,用于对应选项五,刚开始使用以前学习的方法来求交点坐标,但是始终有一个测试点无法通过,后面通过学习csdn上求交点的方法通过了测试点。还要注意题目意思是该交点在两条线段中的一条内就行。
优缺点:
优点:1.运用point类让程序结构不会出现太多重复创建点的代码,但还是存在一些。
2.对非法格式和选项的方法进行详细分析,找出多种可能存在的情况。
缺点:1.程序过长,每个方法都创建了大量double型数据,过于繁杂。
2.选项五求交点的方法使用平常数学方法不能通过测试点,需使用另外的方法,测试样例能通过,但测试点却无法通过。
3.没有使用正则表达式匹配输入格式,代码太过于长。
题目集三:
7-3 点线形系列3-三角形的计算 (48 分)
用户输入一组选项和数据,进行与三角形有关的计算。选项包括:
1:输入三个点坐标,判断是否是等腰三角形、等边三角形,判断结果输出true/false,两个结果之间以一个英文空格符分隔。
2:输入三个点坐标,输出周长、面积、重心坐标,三个参数之间以一个英文空格分隔,坐标之间以英文","分隔。
3:输入三个点坐标,输出是钝角、直角还是锐角三角形,依次输出三个判断结果(true/false),以一个英文空格分隔,
4:输入五个点坐标,输出前两个点所在的直线与三个点所构成的三角形相交的交点数量,如果交点有两个,则按面积大小依次输出三角形被直线分割成两部分的面积。若直线与三角形一条线重合,输出"The point is on the edge of the triangle"
5:输入四个点坐标,输出第一个是否在后三个点所构成的三角形的内部(输出in the triangle/outof triangle)。
必须使用射线法,原理:由第一个点往任一方向做一射线,射线与三角形的边的交点(不含点本身)数量如果为1,则在三角形内部。如果交点有两个或0个,则在三角形之外。若点在三角形的某条边上,输出"on the triangle"
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔,点与点之间以一个英文空格分隔。
输出格式:
基本输出格式见每种选项的描述。
异常情况输出:
如果不符合基本格式,输出"Wrong Format"。
如果符合基本格式,但输入点的数量不符合要求,输出"wrong number of points"。
如果输入的三个点无法构成三角形,输出"data error"。
注意:输出的数据若小数点后超过6位,只保留小数点后6位,多余部分采用四舍五入规则进到最低位。小数点后若不足6位,按原始位数显示,不必补齐。例如:1/3的结果按格式输出为 0.333333,1.0按格式输出为1.0
选项4中所输入线的两个点坐标重合,输出"points coincide",
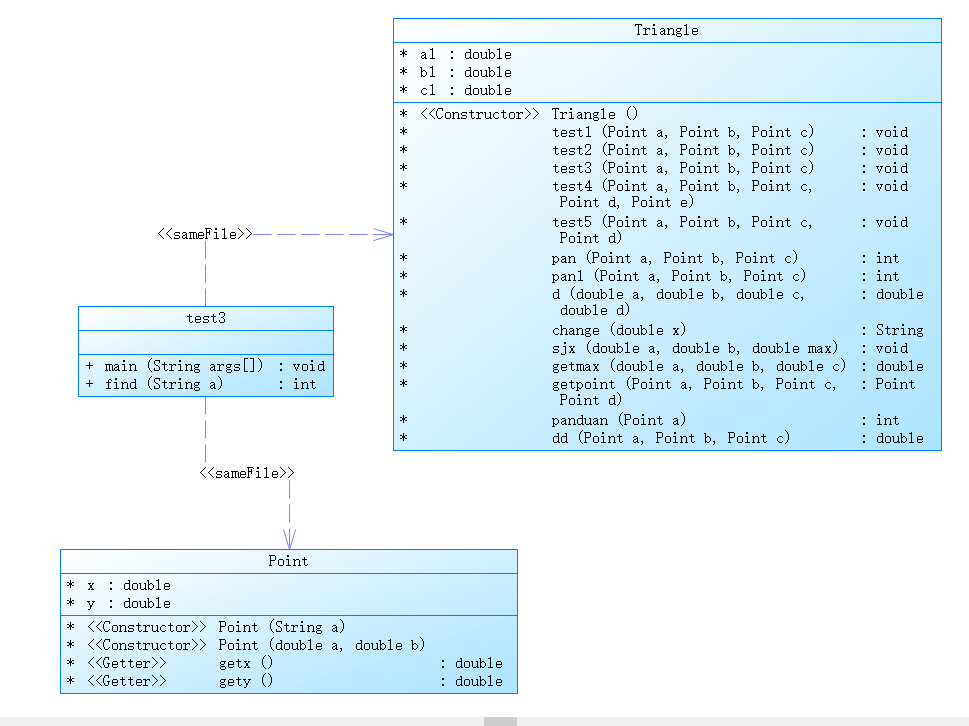
度量分析:
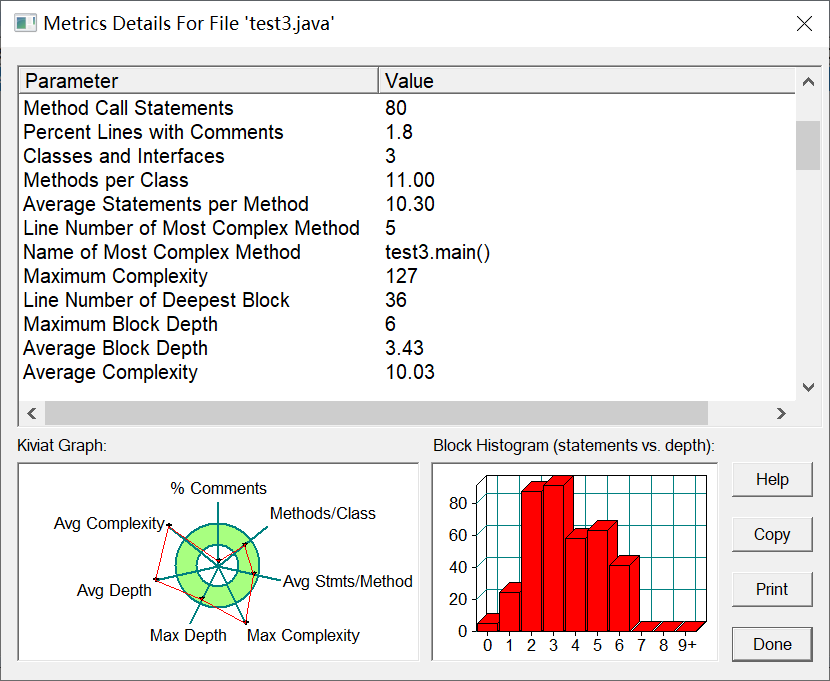
该题目看起来容易,做起来却不尽如人意,判断非法格式判断方面套以7-2的方法改变点的数量和数据格式长度等,能够通过测试点测试样例。我创建了Point类和Triangle类,Triangle类里创建了匹配选项1-5的方法和需要使用的一些方法,并引用Point类创建的点,选项二和四输出的数据需要四舍五入并且保留至小数点后六位,通过在网上查询四舍五入的方法,通过先转换成字符串,再判断是否超过六位小数点,对其进行四舍五入,再输出数据。选项三输出三角形同样因为精度问题需要比较其误差,而选项五耗费很长时间编写的代码通过其测试样例,但始终无法通过测试点,更改了多种方法还是无法完成那两个测试点。
主要代码分析:
class Triangle{ double a1,b1,c1; Triangle(){ } void test1(Point a,Point b,Point c) { int x=0,y=0; a1=d(a.x,a.y,b.x,b.y); b1=d(a.x,a.y,c.x,c.y); c1=d(b.x,b.y,c.x,c.y); if((a.x==b.x&&a.y==b.y)||(a.x==c.x&&a.y==c.y)||(c.x==b.x&&c.y==b.y)) { System.out.println("data error"); } else { if(a1==b1&&b1==c1) { y=1; } if(a1==b1||a1==c1||b1==c1) { x=1; } if(x==1&&y==1) { System.out.println("true true"); } else if(x==1&&y==0) { System.out.println("true false"); } else if(x==0&&y==1) { System.out.println("false true"); } else { System.out.println("false false"); } } } void test2(Point a,Point b,Point c) { double S,C,x1,y1; a1=d(a.x,a.y,b.x,b.y); b1=d(a.x,a.y,c.x,c.y); c1=d(b.x,b.y,c.x,c.y); if((a.x==b.x&&a.y==b.y)||(a.x==c.x&&a.y==c.y)||(c.x==b.x&&c.y==b.y)) { System.out.println("data error"); } else { C=a1+b1+c1; double xx=d(b.x,b.y,c.x,c.y); S=dd(a,b,c)*xx/2; x1=(a.x+b.x+c.x)/3; y1=(a.y+b.y+c.y)/3; String result1= change(C); String result2= change(S); String result3= change(x1); String result4= change(y1); System.out.println(result1+" "+result2+" "+result3+","+result4); } } void test3(Point a,Point b,Point c) { a1=d(a.x,a.y,b.x,b.y); b1=d(a.x,a.y,c.x,c.y); c1=d(b.x,b.y,c.x,c.y); if((a.x==b.x&&a.y==b.y)||(a.x==c.x&&a.y==c.y)||(c.x==b.x&&c.y==b.y)) { System.out.println("data error"); } else { double max=getmax(a1,b1,c1); if(max==a1) { sjx(b1,c1,max); } else if(max==b1) { sjx(a1,c1,max); } else { sjx(a1,b1,max); } } } void test4(Point a,Point b,Point c,Point d,Point e) { int i=0; if(a.x==b.x&&b.y==a.y) { System.out.println("points coincide"); } else if((c.x==d.x&&c.y==d.y)||(c.x==e.x&&c.y==e.y)||(d.x==e.x&&d.y==e.y)){ System.out.println("data error"); } else { int a1=0,a2=0; Point p1=getpoint(a,b,c,d); Point p2=getpoint(a,b,c,e); Point p3=getpoint(a,b,d,e); i=panduan(p1)+panduan(p2)+panduan(p3); if((p1!=null&&p2!=null&&p1.x==p2.x&&p1.y==p2.y)||(p1!=null&&p3!=null&&p1.x==p3.x&&p1.y==p3.y)) { i--; a1=1; } if(p2!=null&&p3!=null&&p2.x==p3.x&&p2.y==p3.y) { i--; a2=1; } if(i<2) { System.out.println(i); } else if(i==2) { if(panduan(p1)==0||a1==1) { double xx=d(d.x,d.y,e.x,e.y); double s=dd(c,d,e)*xx/2; double xx1=d(p2.x,p2.y,p3.x,p3.y); double s1=dd(e,p2,p3)*xx1/2; double s2=s-s1; double max=Math.max(s1, s2); String result1= change(s2); String result2= change(max); String result3= change(s1); if(max==s1) { System.out.println(i+" "+result1+" "+result2); } else { System.out.println(i+" "+result3+" "+result2); } } else if(panduan(p2)==0||a2==1) { double xx=d(d.x,d.y,e.x,e.y); double s=dd(c,d,e)*xx/2; double xx1=d(p1.x,p1.y,p3.x,p3.y); double s1=dd(d,p1,p3)*xx1/2; double s2=s-s1; double max=Math.max(s1, s2); String result1= change(s2); String result2= change(max); String result3= change(s1); if(max==s1) { System.out.println(i+" "+result1+" "+result2); } else { System.out.println(i+" "+result3+" "+result2); } } else if(panduan(p3)==0) { double xx=d(d.x,d.y,e.x,e.y); double s=dd(c,d,e)*xx/2; double xx1=d(p1.x,p1.y,p2.x,p2.y); double s1=dd(c,p1,p2)*xx1/2; double s2=s-s1; double max=Math.max(s1, s2); String result1= change(s2); String result2= change(max); String result3= change(s1); if(max==s1) { System.out.println(i+" "+result1+" "+result2); } else { System.out.println(i+" "+result3+" "+result2); } } } else { System.out.println("The point is on the edge of the triangle"); } } } void test5(Point a,Point b,Point c,Point d) { if((b.x==c.x&&b.y==c.y)||(b.x==d.x&&b.y==d.y)||(d.x==c.x&&d.y==c.y)) { System.out.println("data error"); } else { if((pan(a,b,c)==1&&(b.x!=c.x)&&pan1(a,b,c)==1)||(pan(a,b,d)==1&&(b.x!=d.x)&&pan1(a,b,d)==1)||(pan(a,c,d)==1&&(c.x!=d.x)&&pan1(a,c,d)==1)) { System.out.println("on the triangle"); } else if((b.x==c.x&&a.x==b.x&&pan(a,b,c)==1)||(b.x==d.x&&a.x==b.x&&pan(a,b,d)==1)||(c.x==d.x&&a.x==c.x&&pan(a,c,d)==1)) { System.out.println("on the triangle"); } else { double s1,s2,s3,S; double x1=d(b.x,b.y,c.x,c.y); s1=dd(a,b,c)*x1/2; double x2=d(b.x,b.y,d.x,d.y); s2=dd(a,b,d)*x2/2; double x3=d(c.x,c.y,d.x,d.y); s3=dd(a,c,d)*x3/2; double xx=d(c.x,c.y,d.x,d.y); S=dd(b,c,d)*xx/2; if(s1+s2+s3-S<0.00001) { System.out.println("in the triangle"); } else { System.out.println("outof the triangle"); } } } } int pan(Point a,Point b,Point c) {//判断a是否在b,c点范围内 double max1=Math.max(b.x,c.x); double min1=Math.min(b.x,c.x); double max2=Math.max(b.y,c.y); double min2=Math.min(b.y,c.y); if(a.x>=min1&&a.x<=max1&&a.y>=min2&&a.y<=max2) { return 1; } return 0; } int pan1(Point a,Point b,Point c) {//判断a点是否在b,c点连线的直线上 double k1=(b.y-c.y)/(b.x-c.x); double b1=b.y-k1*b.x; if((k1*a.x)-a.y+b1==0) { return 1; } return 0; } double d(double a,double b,double c,double d) {//计算两点间的距离 return Math.sqrt(Math.pow(a-c, 2)+Math.pow(b-d, 2)); } String change(double x) {//改变数据位数 String a=String.valueOf(x); if(a.length()>6) { return String.format("%.6f",x); } return a; } void sjx(double a,double b,double max) {//判断该三角形为什么类型 if((a*a+b*b)-max*max<-0.00001) { System.out.println("true false false"); } else if(Math.abs((a*a+b*b)-max*max)<0.00001) { System.out.println("false true false"); } else { System.out.println("false false true"); } } double getmax(double a,double b,double c){//求三个数的最大值 double max=a; if(max<b) { max=b; } if(max<c) { max=c; } return max; } Point getpoint(Point a,Point b,Point c,Point d) {//计算交点 if((a.x==b.x&&c.x==d.x)||(a.x==b.x&&b.x==c.x&&c.x==d.x)||(a.y-b.y)/(a.x-b.x)==(c.y-d.y)/(c.x-d.x)) { return null; } else { double aa1,aa2,bb1,bb2,c1,c2,m,x,y; aa1=b.y-a.y; aa2=d.y-c.y; bb1=b.x-a.x; bb2=d.x-c.x; c1=bb1*a.y-aa1*a.x; c2=bb2*c.y-aa2*c.x; m=aa1*bb2-aa2*bb1; x=(bb1*c2-bb2*c1)/m; y=(aa1*c2-aa2*c1)/m; double max3=Math.max(c.x,d.x); double min3=Math.min(c.x,d.x); double max4=Math.max(c.y,d.y); double min4=Math.min(c.y,d.y); if ((x>=min3&&x<=max3&&y>=min4&&y<=max4)) { return new Point(x,y); } else { return null; } } } int panduan(Point a) {//判断是否存在交点 if(a==null) { return 0; } else return 1; } double dd(Point a,Point b,Point c) {//求点到直线的距离 double d; if(b.x==c.x) { d=Math.abs(a.x-b.x); } else { d=Math.abs(((b.y-c.y)/(b.x-c.x))*a.x-a.y+b.y-b.x*((b.y-c.y)/(b.x-c.x)))/Math.sqrt(Math.pow((b.y-c.y)/(b.x-c.x),2)+1); } return d; } }
代码思路:
test1方法简单,只需进行正常的边长比较。test2输出数据时需要注意格式,算重心坐标直接使用数学公式套用,test3类似与前面题目的三角形类型判断,使用了a平方b平方c平方关系的比较,不过测定数据更加严谨,对三种情况都有误差的检验。test4我使用的求交点方法会计算出重复交点,所以运用了标识符进行排除。test5计算点重合和是否在三角形边上大概都过了测试点,而到了计算在三角形内部还是外部时候,由于对射线法不是很能理解,使用别的方法,但是始终无法通过选项五判断的全部测试点。
优缺点:
优点:1.对每个方法的计算严谨,尽量减少了存在的误差。
2.使用了面向过程,创建多个类,进行协同完成。
缺点:1.没有使用正则表达式,代码过于繁琐。
2.对选项五的测试点无法通过,不能使用射线法进行解题。
采坑心得
题目集一 7-7:

此题目唯一容易失分的就是未对double类型数据计算精度的把握,使用勾股定理进行计算判断直角三角形会存在误差,使用以后遇到类似判断直角三角形乃至double型数据计算时需要算其精度,把握误差,可以将误差设为0.00001或者更小。
题目集二 7-2:

此题目奇偶效验性判断的时候要注意不仅有效数据还有有效数据后一位,共九位都需要进行判断,并且这个是嵌套循环,使用每判断完一串有效数据后k需要加10,进行下一段字符串的判断,这个坑就是需要注意循环时数据判断位数准确,并且要正确理解题目含义。
题目集三 7-1:
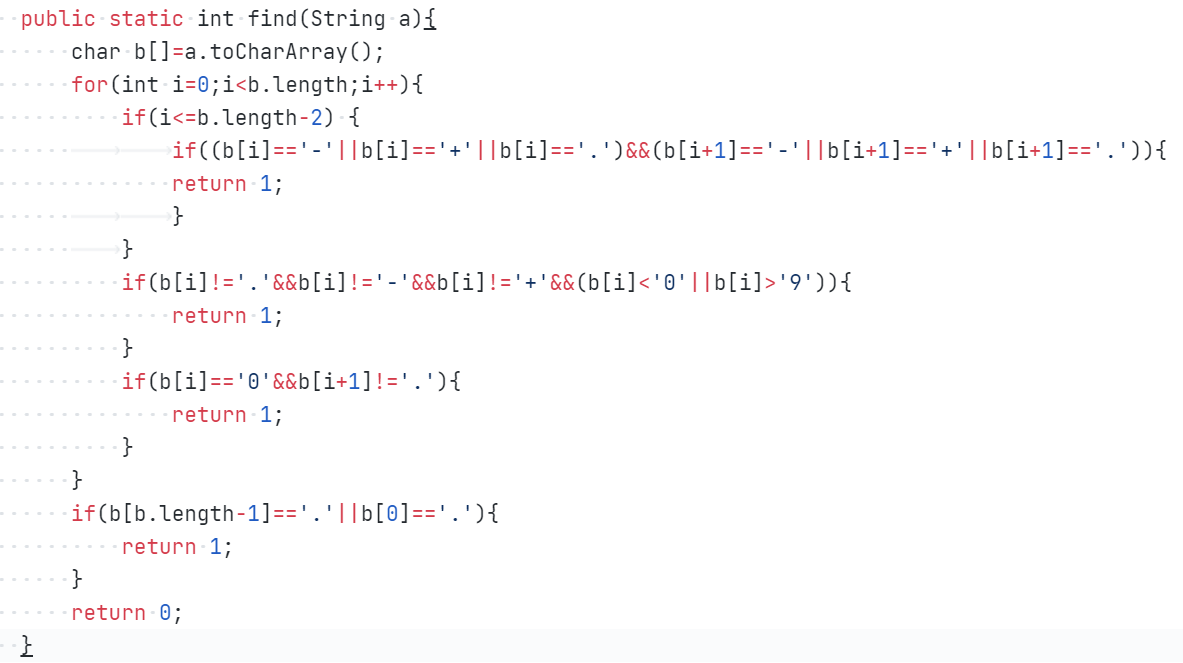
该题目判断非法格式时,对格式的判断过于复杂且不够正确,使用了许多if语句,导致代码太长,对整个输入格式的考虑不周全,容易存在隐患。所以以后做类似非法格式判断的题目应该学习正则表达式用来判断输入格式的合法性,减少过多的代码,让整个程序都看起来简洁明了,注意输入格式字符的前后顺序。
题目集三 7-2:

1.用前一题的非法判断方法发现无法通过全部测试点存在bug,所以对find方法进行改进。此处坑点在于我们对输入格式判断时应该循循渐进,可以一位连着一位判断,避免有遗漏的情况发生。

2.在对选项五计算交点时候,运用平常所学的求交点坐标貌似行不通无法通过两个测试点,我通过网上查询方法才找寻到这个能够过测试点求交点的方法。故我们应该多学习算法,不要纠结于一种算法或只掌握一种算法。以后遇到此类算交点的题目时可采用这种方法。
题目集三 7-3:

1.此部分与前面求三角形类型的相似,我一开始只是把握了直角三角形的精度,但是有测试点未通过,然后我就增加了其他判断时的精度,最后通过了测试点。这题精度不仅计算了直角三角形,还涉及钝角三角形的精度,所以以后对于double型都应该注意精度,来确保准确性。

2.因为不会射线法,我通过使用面积法来判断点在内部还是外部,用这种方法我输入5:0.5,0.5 0,0 0,2 4,0能够输出in the triangle,输入5:0,0 -1,-1 2,3 3,4能够输出outof the triangle,两个测试样例都通过了,但是有两个测试点却始终无法通过,于是更改了多张方法还是无法通过。此处坑点在于该题应该设定了测试射线法的点,故使用其他方法无法通过,应该学习射线法去完成题目。
改进建议
题目集一7-7和题目集二7-2:
由SourceMonitor以及PowerDesigner软件测评结果可以得知,代码复杂度过高,使用了太多if-else语句,且只有一个Main类,建议减少使用if-else语句,并且可以使用switch语句来减少使用,可以创建输出类和判断类,进行多种类交互。
题目集三7-1、题目集三7-2和题目集三7-3:
由SourceMonitor的评测图以及PowerDesigner软件测评结果可以可知,这几个题目的圈复杂度之高,因为使用的是普通的if-else语句,并且类设计的也十分简陋,大致跟面向过程差不多,应该使用switch语句进行选项进行选择的判断,并且可以再创建方法类和线类,进行交互使用,让复杂度降低,让代码简洁明了。我写的代码与代码间关系过于简单,也没有使用正则表达式,代码太过繁杂,在以后的学习中,做此类题目应该使用正则表达式降低代码繁杂和复杂度,也要多将类与类之间的关系进行调用,体现java面向对象的特点。
总结
java这阶段的学习,老师主要讲的是对象与类和面向对象的两章,学习的都是java的基础知识,但是却是java的奠基石,只有学好这些基础的类知识,才能为后面更好的学习做准备,让我从之前学C语言的习惯改到面向对象的java,我对java的了解还很浅显,需要学习更多的结构、语法知识来充实java的学习。
这几次的题目集,让我明白了许多还需要提高的地方:
1.垃圾代码过多,因为不熟悉类与类之间的关系和调用,使用过多语句,代码太过复杂,写的代码质量低,要懂得多运用类与类的关系。
2.多用switch语句,减少if-else语句的使用,这几次代码复杂度都很高,要写的更加简洁。
3.使用正则表达式来解决一些非法格式判断问题,使用平常方法代码繁杂且效率低,而正则表达式能够将输入的字符串快速判断。
4.上课认真听课,课后也需要自己多了解java的知识,毕竟老师一般教基础知识,许多知识还需要自学,多巩固基础函数语法知识,许多都与C语言类似,更易于理解和吸收,防止在平常编写代码时忘记一些基础知识。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号