转载读书笔记《宽度学习：原理与实现》陈俊龙
摘要：宽度学习是一种不依赖深度结构的神经网络结构，其优秀的运算速度和简洁的结构可以说是机器学习界的一股清流。本文将从原理和代码实现的角度对其进行分析和梳理，由于笔者水平有限，不足之处还望各位楷正。
首先，放一些很好的参考资料连接：
- 澳门大学陈俊龙：无需深度结构的高效增量学习系统 | 雷锋网 雷锋网对于宽度学习的介绍，很详细很具体
- Broad Learning System: An Effective and Efficient Incremental Learning System Without the Need for Deep Architecture 陈俊龙老师IEEE NNLS 论文
- Home-Broadlearning BLS主页
相对于“深度”结构来说，“宽度”结构由于没有层与层之间的耦合而非常简洁。同样，由于没有多层连接，宽度网络亦不需要利用梯度下降来更新权值，所以计算速度大大优于深度学习。在网络精度达不到要求时，可以通过增加网络的“宽度”来提升精度，而增加宽度所增加的计算量和深度网络增加层数相比，可以说是微乎其微。笔者认为，宽度学习适用于数据特征不多但对预测实时性要求较高的系统。也就说，该结构在类似ImageNet的大型图像分类问题上表现并不是很好，这也是为什么原文中只有MNIST和NORB数据集实验结果的原因。
本文的变量表示和公式推导可能与陈老师论文中有所出入，这是因为本文是根据陈老师的开源代码进行的推导，而不是对论文中的内容。这里如有错误欢迎指正。
0. 一些重要的概念
宽度网络的实质是一种随机向量函数链接神经网络（random vector functional link neural network，RVFLNN）。与CNN不同，该网络并不通过反向传递改变特征提取器的核，而是通过求伪逆计算每个特征节点和增强节点的权重。这就好比我们找来100个不懂数学的孩子，他们对于任何问题（如1+1=？）的回答都是0-9中的任意一个数字，但这些孩子有自己的偏好，也就是说，他们回答的随机分布不同。网络的目的就是如何通过这100个孩子的回答预测出所提问题的答案。
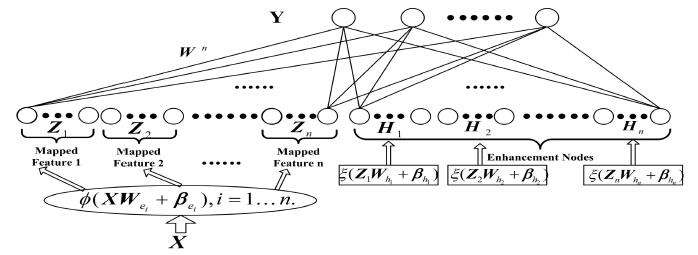宽度学习网络结构图：每个网络的输入由特征节点与增强节点构成
这里有几个重要的名词和变量将在后面的叙述中经常用到：
:每个窗口特征节点的个数。
:特征节点的窗口个数。
:增强节点个数。
:训练集，s表示样本个数，f表示特征数。对于图像这样的2维数据，代码中将其按行拉成了一维向量。
1. 生成特征节点
宽度学习的核心就是求特征节点和增强节点到目标值的伪逆。在这里，特征节点和增强节点相对应的是神经网络的输入，求得的逆矩阵相当于神经网络的权值。那么首先，我们需要建立输入数据到特征节点的映射。
首先，对 进行z分数标准化，这里必须确保输入数据已经归一化到0到1之间。
接着，对 进行增广，在训练集最后增加一列1，使之变为
，这样做是为了在生成特征节点时可以直接通过矩阵运算增加偏置项。
然后，开始为每个窗口生成特征节点：
1. 生成随机权重矩阵 :
是一个
维的随机权重矩阵，其值呈高斯分布；
2. 将 放入
中，i表示迭代量，迭代次数为
；
3. ；
这里笔者认为是对每个样本的特征进行了一次权值随机的卷积和偏置，得到了新的特征。如果我们把A1和H1展开表示就会发现对于每个样本 ，新特征都可以表示为：
这体现了整个网络的特性： 随机向量函数链接。
4. 对A1进行行归一化；
5. 对A1进行稀疏表示（sparse autoencoder）；
这也是整个特征节点生成中比较核心的问题之一，对于稀疏表示的原因，陈老师在论文中是这样解释的：
To overcome the randomness nature, the sparse autoencoder could be regarded as an important tool to slightly fine-tune the random features to a set of sparse and compact features. Specifically, sparse feature learning models have been attractive that could explore essential characterization.
一句话，为了解决网络随机性所带来的问题。笔者认为，稀疏表示可以有效减少新生成特征节点的线性相关程度，使得新生成的节点不至于过于“浪费”。
论文中采用了lasso方法来解决稀疏表示过程中的优化问题。此时我们有新生成的随机特征向量 ,维数为
，还有之前增广之后的训练集
,维数为
。那么稀疏表示的目的就是找到一个稀疏矩阵
使得
。所要求得W可以通过最优化求解：
。
6. 最终生成一个窗口得特征节点 ：
，其中normal表示归一化，每个窗口特征节点的归一化方法记为
。
对于 个特征窗口，我们都生成
个特征节点，每个节点是s维特征向量。这样，对于整个网络，特征节点矩阵
就是一个维数为
的矩阵。
2. 生成增强节点
宽度网络的另一特性，就是可以利用增强节点对随机的特征节点进行补充。通过上文我们发现，特征节点都是线性的，而引入增强节点的目的就是为了增加网络中的非线性因素。
1. 与特征节点一样，首先对特征节点矩阵 进行标准化与增广，得到
。与特征节点不同，增强节点的系数矩阵不是随机矩阵，而是经过正交规范化后的随机矩阵。假设
,则增强节点的系数矩阵
可以表示为
维经过正交规范化的随机矩阵。笔者认为这样做的目的是将特征节点通过非线性映射到一个高维的子空间，使得网络的表达能力更强以起到“增强”的目的。
2. 对增强节点进行激活： ；
这里的 被称作增强节点的缩放尺度（shrinkage scale of the enhancement nodes），是网络中可调参数之一。tansig是BP神经网络中常用的一种激活函数，所以笔者把这一步理解为神经网络中的激活操作，可以最大程度将增强节点所表达的特征进行激活。
3. 最终生成网络的输入
与特征节点相比，增强节点并不与要稀疏表示，也不需要进行窗口迭代。虽然正交化的迭代也会耗费一些计算时间，但增加增强节点所需的计算时间，往往少于增加特征节点。网络最终的输入 可以表示为
，每个样本的特征维度为
。
3. 求伪逆(pseudoinverse)
神经网络的目的就是要求得输入到输出的映射。拿分类问题来说，当输入量为X，标签向量为Y时，如果能得到 中的W话，那么这个网络也就完成了。看上去这个问题很简单，
就大功告成了。但实际情况是，X往往求不出逆或者根本没有逆，那么W的求解就需要X的伪逆。伪逆的求法在论文中是这样描述的：
原文中关于伪逆的求法
其实，实际实现的方式很简单，假设 xx为网络的输出值，即 ，则：
，其中Y为训练集的标签。这样，整个网络的输入和权重就训练完成了。
4. 测试
训练完成之后，需要保存的参数其实只有W和ps，所以相比于深度学习，网络参数量很少。通过参数的维度可以发现，W是一个维度为 的矩阵(n为分类类别数)，也就是说，他与训练集样本数s无关。这就意味着我们可以按照训练的步骤生成特征和增强节点，再利用
进行预测。只不过在特征节点生成的时候，要按照先前的归一化标准ps进行生成。
5. 多说两句
分析完这个算法，我的第一感觉是思路清晰简洁又让人眼前一亮。之前学习深度学习时，感觉近几年算法越来越复杂，各种创新层出不穷，但鲜有在网络结构上的颠覆性创新。虽然说目前BLS作为一种挑战DLS的结构，还略显稚嫩，但我相信好的方法一定是简明而优美的，数学的本质亦是如此。
