KMP

KMP

kmp是快速在s[]长文本中匹配p[]模式串，并返回起始坐标

朴素算法：

for (int i = 1; i <= m; i ++ )
{
    bool flag = true;
    for (int j = 1; j <= n; j ++ )
        if (s[i] != p[j])
        {
            flag = false;
            break;
        }
}

朴素算法每次第二层循环后j指针还要往回退

kmp可以不需要每次退回p[0]

如何求

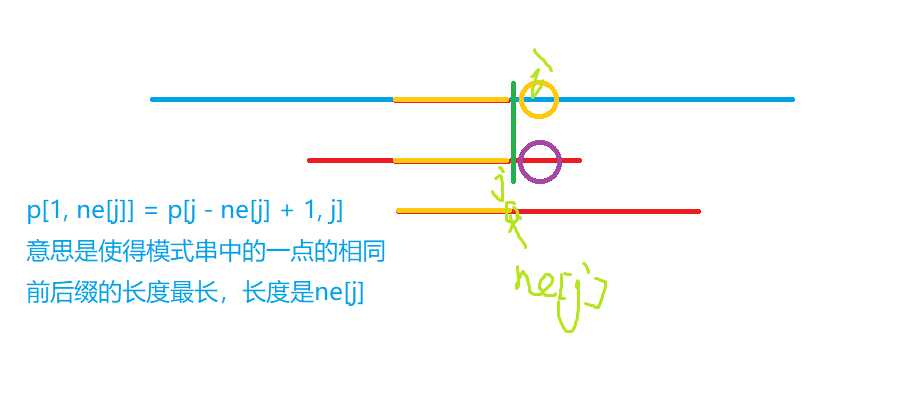
代码如下：

// i表示s的指针，j表示p的指针，m是s的长度，n是p的长度
for (int i = 1, j = 0; i <= m; i ++ ) // i总比j先走一步
{
    while (j && s[i] != p[j + 1]) j = ne[j];
    if (s[i] == p[j + 1]) j ++ ;
    if (j == n)
    {
        // 匹配成功
    }
}

如何初始化next

因为上一段代码求的就是前缀和后缀相等的最大值，所以我们可以用这种思想应用到一个数组上，从而求出next

代码如下：

for (int i = 2, j = 0; i <= n; i ++ )
{
    while (j && p[i] != p[j + 1]) j = ne[j];
    if (p[i] == p[j + 1]) j ++ ;
    ne[i] = j;
}

模板题的完整代码：

#include <iostream>
 
using namespace std;
 
const int N = 100010, M = 1000010;
 
int n, m;
char p[N], s[M];
int ne[N];
 
int main()
{
    cin >> n >> p + 1 >> m >> s + 1;
    
    // 求next数组
    for (int i = 2, j = 0; i <= n; i ++ )
    {
        while (j && p[i] != p[j + 1]) j = ne[j];
        if (p[i] == p[j + 1]) j ++ ;
        ne[i] = j;
    }
    
    // 求答案
    for (int i = 1, j = 0; i <= m; i ++ )
    {
        while (j && s[i] != p[j + 1]) j = ne[j];
        if (s[i] == p[j + 1]) j ++ ;
        if (j == n)
        {
            printf("%d ", i - n + 1);
            j = ne[j]; // 因为还要做下一个，所以继续更新一下ne
        }
    }
    
    return 0;
}