乘风破浪:LeetCode真题_010_Regular Expression Matching
乘风破浪:LeetCode真题_010_Regular Expression Matching
一、前言
关于正则表达式我们使用得非常多,但是如果让我们自己写一个,却是有非常大的困难的,我们可能想到状态机,确定,非确定状态机确实是一种解决方法,不过需要消耗很大的时间去推理和计算,对于正则表达式的缩小版,我们往往可以通过递归,递推,动态规划等方法来解决。
二、Regular Expression Matching
2.1 问题理解




2.2 问题分析和解决
遇到这样的问题,我们想到了递归,对于.是很好处理和匹配的,但是如果和*结合起来就变化无穷了,正是因为*我们才要递归。
让我们看看官方的答案:
class Solution {
public boolean isMatch(String text, String pattern) {
if (pattern.isEmpty()) return text.isEmpty();
boolean first_match = (!text.isEmpty() &&
(pattern.charAt(0) == text.charAt(0) || pattern.charAt(0) == '.'));
if (pattern.length() >= 2 && pattern.charAt(1) == '*'){
return (isMatch(text, pattern.substring(2)) ||
(first_match && isMatch(text.substring(1), pattern)));
} else {
return first_match && isMatch(text.substring(1), pattern.substring(1));
}
}
}
如果模式串和源串第一个字符能够正常匹配,并且不为空,模式串的第二个字符不为'*',那么我们可以继续递归匹配下面的东西:
1 return first_match && isMatch(text.substring(1), pattern.substring(1));
如果模式串的长度大于1,并且第二个字符是*,那么我们就有可能匹配到源串的很多的字符,也就相当于将源串已经匹配的去掉,拿剩下的和整个模式串继续比较,此时*发挥了作用,或者比较源串与去掉了*的模式串,因为*没有能够发挥作用。于是就得到了:
1 if (pattern.length() >= 2 && pattern.charAt(1) == '*'){ 2 return (isMatch(text, pattern.substring(2)) || 3 (first_match && isMatch(text.substring(1), pattern))); 4 }

除此之外我们还可以使用动态规划算法:
class Solution {
public boolean isMatch(String text, String pattern) {
boolean[][] dp = new boolean[text.length() + 1][pattern.length() + 1];
dp[text.length()][pattern.length()] = true;
for (int i = text.length(); i >= 0; i--){
for (int j = pattern.length() - 1; j >= 0; j--){
boolean first_match = (i < text.length() &&
(pattern.charAt(j) == text.charAt(i) ||
pattern.charAt(j) == '.'));
if (j + 1 < pattern.length() && pattern.charAt(j+1) == '*'){
dp[i][j] = dp[i][j+2] || first_match && dp[i+1][j];
} else {
dp[i][j] = first_match && dp[i+1][j+1];
}
}
}
return dp[0][0];
}
}
首先我们定义dp[i][j]代表源串T[i:]和模式串P[j:]是匹配的,其中i,j为源串和模式串的下标,于是我们只要求得dp[0][0]的值就可以了。我们已知的条件是:
dp[text.length()][pattern.length()] = true;
于是我们从后往前倒求最终的dp[0][0],通过如下的判断,看看是哪一种情况,然后根据相应的情况采取不同的递推策略,最终得到结果:
1 boolean first_match = (i < text.length() && 2 (pattern.charAt(j) == text.charAt(i) || 3 pattern.charAt(j) == '.')); 4 if (j + 1 < pattern.length() && pattern.charAt(j+1) == '*'){ 5 dp[i][j] = dp[i][j+2] || first_match && dp[i+1][j]; 6 } else { 7 dp[i][j] = first_match && dp[i+1][j+1]; 8 }

同样的我们算法也是使用了递归和动态规划:
在动态规划方面我们使用match[i]来表示对于源串从i到最后(T[i:])都是能够匹配的,于是之用求match[0]即可。
import java.util.Arrays;
public class Solution {
/**
* Implement regular expression matching with support for '.' and '*'.
* '.' Matches any single character.
* '*' Matches zero or more of the preceding element.
*
* 题目大意:
* 实现一个正则表达式匹配算法,.匹配任意一个字符,*匹配0个或者多个前导字符
*/
public boolean isMatch(String s, String p) {
boolean[] match = new boolean[s.length() + 1];
Arrays.fill(match, false);
match[s.length()] = true;//刚开始满足需要
for (int i = p.length() - 1; i >= 0; i--) {
if (p.charAt(i) == '*') {
for (int j = s.length() - 1; j >= 0; j--) {
//原来就是false只有能够为真,才为真。
match[j] = match[j] || match[j + 1]
&& (p.charAt(i - 1) == '.' || s.charAt(j) == p.charAt(i - 1));
}
i--;
} else {
for (int j = 0; j < s.length(); j++) {
//从前往后,只有到了已经有true的时候才能生效。如果从后往前反而有问题。
match[j] = match[j + 1]
&& (p.charAt(i) == '.' || p.charAt(i) == s.charAt(j));
}
//将最后的置为假,本来就应该不真,便于以后的判断
match[s.length()] = false;
}
}
return match[0];
}
// 下面的代码用时比较长
public boolean isMatch2(String s, String p) {
// 输入都为null
if (s == null && p == null) {
return true;
}
// 有一个为null
else if (s == null || p == null) {
return false;
}
return isMatch(s, 0, p, 0);
}
/**
* 正则表达式匹配
*
* @param s 匹配串
* @param sIdx 当前匹配的位置
* @param p 模式串
* @param pIdx 模式串的匹配位置
* @return 匹配结果
*/
public boolean isMatch(String s, int sIdx, String p, int pIdx) {
// 同时到各自的末尾
if (s.length() == sIdx && p.length() == pIdx) {
return true;
}
// 当匹配串没有到达末尾,模式串已经到了末尾
else if (s.length() != sIdx && p.length() == pIdx) {
return false;
}
// 其它情况
else {
// 如果当前匹配的下一个字符是*号
if (pIdx < p.length() - 1 && p.charAt(pIdx + 1) == '*') {
// 匹配串未结束并且当前字符匹配(字符相等或者是.号)
if (sIdx < s.length() && (s.charAt(sIdx) == p.charAt(pIdx) || p.charAt(pIdx) == '.')) {
return isMatch(s, sIdx + 1, p, pIdx + 2) // 匹配串向前移动一个字符(只匹配一次)
|| isMatch(s, sIdx + 1, p, pIdx) // 匹配串向前移动一个字符(下一次匹配同样的(模式串不动))
|| isMatch(s, sIdx, p, pIdx + 2); // 忽略匹配的模式串
} else {
// 忽略*
return isMatch(s, sIdx, p, pIdx + 2);
}
}
// 匹配一个字符
if (sIdx < s.length() && (s.charAt(sIdx) == p.charAt(pIdx) || p.charAt(pIdx) == '.')) {
return isMatch(s, sIdx + 1, p, pIdx + 1);
}
}
return false;
}
}
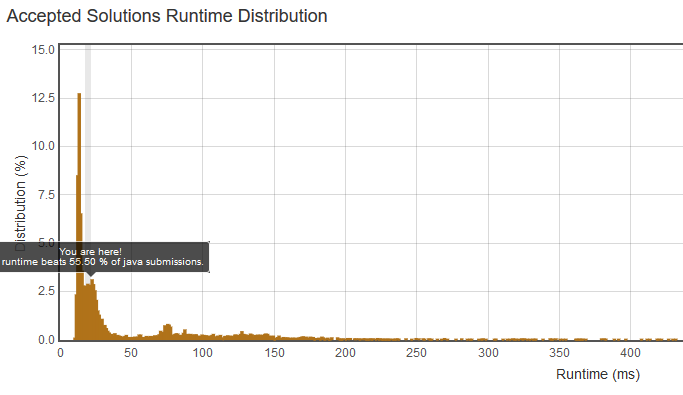
如下表所示,使用递归需要1163ms而使用动态规划需要20ms,差别非常显著。

三、总结
对于一些比较困难的问题,我们需要从不同的角度考虑,解决问题的方法可以从递归,递推,动态规划等方面去考虑。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号