遗传算法

遗传算法

概念

　　遗传算法（genetic algorithms，GA）：一类借鉴生物界自然选择和自然遗传机制的随机搜索算法，非常适用于处理传统搜索方法难以解决的复杂和非线性优化问题。

　　遗传算法可广泛应用于组合优化、机器学习、自适应控制、规划设计和人工生命等领域。

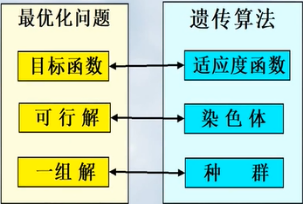
与生物遗传的类比

生物遗传概念    　　　　　　　　遗传算法中的应用

适者生存 　　　　　　　　　　　　　目标值比较大的解被选择的可能性大

个体（Individual） 　　　　　　　　解

染色体（Chromosome） 　　　　　　 解的编码（字符串、向量等）

基因（Gene） 　　　　　　　　　　　解的编码中每一分量

适应性（Fitness） 　　　　　　　　 适应度函数值

群体（Population） 　　　　　　　　根据适应度值选定的一组解

  　　　　　　　　　　　　　　　　（解的个数为群体的规模）

婚配（Marry） 　　　　　　　　　　 交叉（Crossover）选择两个染色体进行

                        交叉产生一组新的染色体的过程

变异（Mutation） 　　　　　　　　　编码的某一分量发生变化的过程

基本思想

　　在求解问题时从多个解开始，然后通过一定的法则进行逐步迭代以产生新的解。

一般步骤

 

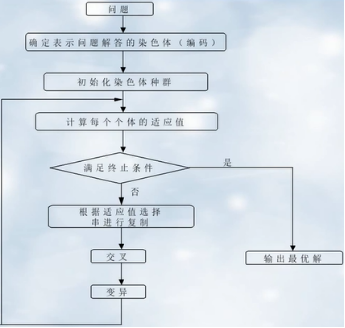
编码

　　由于遗传算法不能直接处理问题空间的参数,因此必须通过编码将要求解的问题表示成遗传空间的染色体或者个体。这一转换操作就叫做编码，也可以称作（问题的）表示（representation）。

 1.位串编码

　　*一维染色体编码方法：将问题空间的参数编码为一维排列的染色体的方法。

　　（1）二进制编码

　　　　用若干二进制数表示一个个体，将原问题的解空间映射到位串空间B = {0，1}上，然后再位串空间上进行遗传操作。

　　　　优点：类似于生物染色体的组成，算法已于用于生物遗传理论解释，遗传操作如交叉、变异等易实现；算法处理的模式数最多。

　　　　缺点：相邻整数的二进制编码可能具有较大的Hamming距离（15：01111 16：10000），降低了遗传算子的搜索效率；要先给出求解的精度；求解高维优化问题的二进制编码串长，算法的搜索效率低。

 　　（2）Gray编码

　　　　将二进制编码通过一个变换进行转换得到的编码。

 2.实数编码

　　采用实数表达法不必进行数制转换，可直接在解的表现型上进行遗传操作。

适应度函数-评价个体的适应度

　欺骗问题  在遗传算法中，将所有妨碍适应度值高的个体产生，从而影响遗传算法正常工作的问题统称为欺骗问题（deceptive problem）。

　过早收敛  缩小这些个体的适应度，以降低这些超级个体的竞争力。

　停滞现象  改变原始适应值的比例关系，以提高个体之间的竞争力。

　适应度函数的尺度变换（fitness scaling）或者定标：

　　对适应度函数的某种映射变换。

　　　　（1）线性变换：ƒ’= aƒ + b  

　　　　　　　　 

 　　　　（2）幂函数变换：ƒ’= ƒ^K

 　　　　（3）指数变换：ƒ’= e^-aƒ

选择

选择操作也称复制（reproduction）操作：从当前群体中按照一定概率选出优良的个体，使它们有机会作为父代繁殖下一代子孙。

　　*判断个体优良与否的准则是各个个体的适应度值：个体适应度越高，其被选择的机会就越多。

　1.个体选择概率分配方法

　　（1）适应度比例方法（fitness proportional medel）或蒙特卡洛法（Monte Carlo）。

　　　　·各个个体被选择的概率和其适应度值成比例。

　　　　·个体i被选择的概率为：　

　　　　　　　　　　　　　　　　

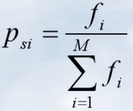
 　　（2）排序方法（rank-based model）

　　　　①线性排序：J.E.Baker

　　　　　　

　　　　②非线性排序：Z.Michalewicz

　　　　　　

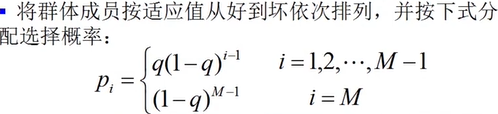
交叉

　基本交叉算子

　　（1）一点交叉（single-point crossover）

　　　　在个体串中随机设定一个交叉点，实行交叉时，该点前或后的两个个体的部分结构进行互换，并生成两个新的个体。

　　（2）二点交叉（two-point crossover）

 　　　　随机设置两个交叉点，将两个交叉点之间的码串相互交换。

 　修正的交叉方法

　　　部分匹配交叉PMX：Goldberg D.E.和R.Lingle(1985)

　　　　

　　　　A’中2，3，9均有两个，是非法个体，修正方法：将外部的重复部分替换成原来被替换掉的值，如将A’中第一个9替换成7。

变异

　（1）位点变异：群体中的个体码串，随机挑选一个或多个基因座，并对这些基因座的基因值以变异概率作变动。

　（2）逆转变异：在个体码串中随机选择两点（逆转点），然后将两点之间的基因值以逆向顺序插入到原位置中。

　（3）插入变异：在个体码串中随机选择一个码，然后将此码串插入随机选择的插入点中间。

　（4）互换变异：随机选取染色体的两个基因进行简单互换。

　（5）移动变异：随机选取一个基因，向左或者向右移动一个随机位数。

遗传算法的特点

　　遗传算法是一种全局优化概率算法。

• 　遗传算法所求解的优化问题没有太多的数学要求，由于进化特性，搜索过程中不需要问题的内在性质，无论是线性的还是非线性的，离散的还是连续的都可以处理，可直接对结构对象进行操作。
•   利用随即技术指导对一个被编码的参数空间进行高效率搜索。
•   采用群体搜索策略，易于并行化。
•   仅用适应度函数来评估个体，并在此基础上进行遗传操作，使种群中个体之间进行信息交换。