408算法练习——接雨水

接雨水

问题链接：https://leetcode-cn.com/problems/trapping-rain-water/

一、问题描述

　　给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

　　示例1

　　

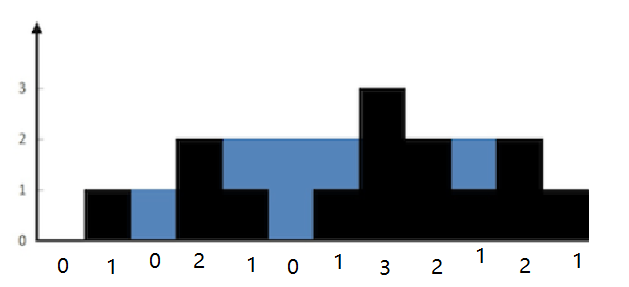
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

 

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

 

二、问题分析

　　这道题和前面的一道题类似，但是又有所不同，这道题中每个墙壁有体积，所以每个位置的容水量是不同的，但是也可以使用双指针来解题，初步的思想是从左向右遍历，使用指针i记录遍历过程中的最高点，j来遍历数组，当j<i时，计算j和i的差值，存入一个结果数组中，当j>i时，更新i=j。但是这个算法的问题很明显，在经过整个数组的最高点后i不再更新，而后面的区间可能并不能容水，就像示例1中，经过3后仍然有区间不能容水，所以我想出的办法是，从后向前再次遍历，但此次遍历只遍历的到最高点，遍历过程中与第一次遍历操作相同，只不过是顺序相反而已，这次遍历的目的就是修复结果数组中出错的值。完成两次遍历后，对结果数组进行求和即可，结果数组中保存了每个点的容水量。

　　进过初步分析后，还可以优化代码，（1）可以先进行一次折半查找，直接找出最大值，这样两边的变量过程都截至在最大值处，从两次变量变为了一次变量。（2）变为一次遍历后可以不使用结果数组，改用变量来代替，因为两端的遍历过程都是求值的过程，免去了修复操作。（3）遍历中的双指针其实有一个指针只是负责记录最大值，那么可以改用一个变量替代该指针，免去了移动指针的操作。

　　进一步优化：考虑快排中双指针的操作，这里把快排中的交换值操作改为计算容水量操作。定义两个指针分别位于数组的两端，先让左指针从左向右遍历，遍历过程中更新最大值和结果变量，然后让右指针向左遍历，同样记录最高值和结果变量。这么做的原因是，我们可以把每个元素的值想象成一个水柱，这个水柱的高度就是我们要统计的，而初始状态下因为两边都没挡水的墙所以水柱的高度都是0，每个端点的容水量取决于这个端点两侧的最低点。

　　请结合代码理解算法思想

三、代码及算法

　　

class Solution {
    public int trap(int[] height) {
        int l=0,r=height.length-1,left_max=0,right_max=0,res=0;
        //l和r为左右指针，两个max用于两侧遍历时记录最高点，res为结果变量
        while(l<r){
            if(height[l]<height[r]){//左侧墙体低，水柱高度取决于左端点，所以从左侧开始遍历
                if(height[l]<left_max){//左侧遍历到的点低于左侧墙壁，这个点就能容水，容水量就是差值
                    res = res+left_max-height[l];
                }else{//否则就是有新的最高点
                    left_max = height[l];
                }
                l++;
            }else{
                if(height[r]<right_max){//与前面同理
                    res = res+right_max-height[r];
                }else{
                    right_max = height[r];
                }
                r--;
            }
        }
        return res;
    }
}