408算法练习——马走日

马走日

一、题目描述

　　假设国际象棋棋盘有5*5共25个格子，设计一个程序，使棋子从初始位置（如图）开始跳马，需要将棋盘格子全走一遍，每个格子只允许走一次，马的走法只能走“日字形”

　　

 

 

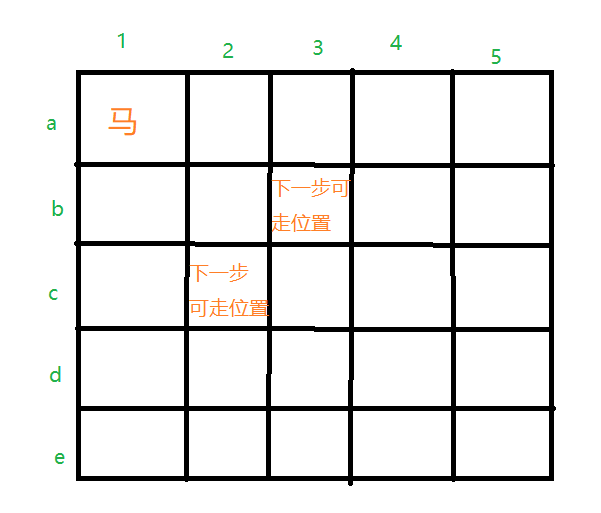
　　问：有多少解

二、解题思路

　　采用回溯法依次试探下一步的走法，如果下一步走法不合理就不再继续而转向上一步走法。

　　基本思想：构造一颗树，这个树包含了所有可能的走法（包括合法和不合法的），然后对树进行深度优先搜索，搜索过程中对于每一个结点判断当前结点的走法是否合法，如果合法就进行下去，如果不合法就返回到父节点转向其他子树。

　　构造一个二维数组，A[5][5]，其中A[i][j]中记录了棋盘第i行第j列是否被走过，马当前位置为h行l列，那么马的可能走法就有[h+2][l+1]；[h+2][l-1]；[h-2][l+1]；[h-2][l-1]；[h+1][l+2]；[h-1][l+2]；[h+1][l-2]；[h-1][l-2]，如图有8种走法，为了方便就假设数组下标从1开始，那么当h和l进行减法或加法运算后如果值小于等于0或大于5都是不合法的。

　　

 

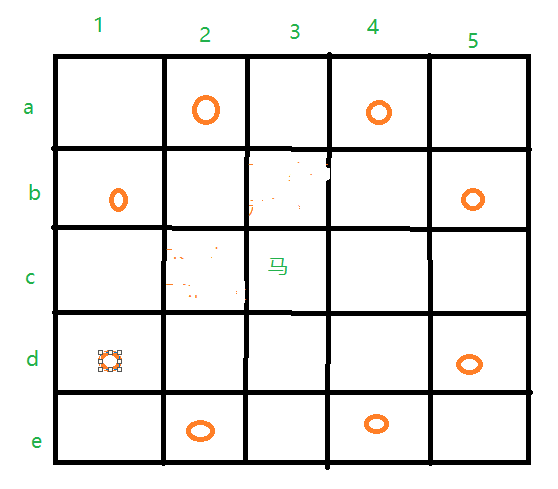
 　　设计回溯算法，递归边界，可以定义一个计数器count，每次跳马，count++，不能跳马的情况有h和l更新后A[h+1][l+2]或者其他值为1，说明走过这个格子，不能往这里跳。h和l越界也不能跳，如果在某个状态下，不能跳马，而且此时count不是25那么就说明这个方案不可行，就该舍弃，如果count达到25，那么说明这个方案可行。

代码：

#include <cstdio>
int A[5][5];//用来记录该格子是否被走过
const int next[8][2] = {{1,2},{1,-2},{-1,2},{-1,-2},{2,1},{2,-1},{-2,1},{-2,-1}}; 
int x,y,res=0;//统计所有可能的走法
bool check(int x,int y){
    if(x>4||x<0||y>4||y<0){//如果发生越界说明此次不合法 
        return false;
    }
    if(A[x][y] == 1){//等于1说明这个格子走过了 
        return false;
    }
    return true;
}
void dfs(int x,int y,int count){
    if (count == 25){
        res++;
        return;
    }
    for(int i=0;i<8;i++){
        int next_x = x+next[i][0];
        int next_y = y+next[i][1];
        if(check(next_x,next_y)){
            A[next_x][next_y] = 1;
            dfs(next_x,next_y,count+1);
            A[next_x][next_y] = 0;//在进行过判断后将A数组改回来用于下一次遍历，注意理解这行代码，该行为关键行
        }
    }
} 

int main(){
    A[0][0] = 1;
    dfs(0,0,1);
    printf("%d",res);
    return 0;
}

最终结果为304