leetcode每日一题(2021.5.17)——x的平方根

题目：x的平方根（简单）

一、问题描述

实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例 1:

输入: 4
输出: 2
示例 2:

输入: 8
输出: 2
说明: 8 的平方根是 2.82842...,
  由于返回类型是整数，小数部分将被舍去。

 

二、解题思路

　　可以思考我们平时求根的思路，比如9，9/1=9；9/2=4.5；9/3=3。此时商和除数相等，就得出9的平方根，不妨继续往后除试试，9/4=2.25；9/5=1.8……不难发现当得出平方根继续往后除时，商会小于除数。

　　总结以上规律，那么就会想到，是否对于所有的数都有这个规律？可以用计算器试试

　　下面开始尝试编写代码：

　　　　设计一个循环，i为自增变量，让x每次循环都除i，当x/i的值小于等于i时终止循环，此时的商就是题目要求的平方根。

 

三、代码

　　

 

 　　

 

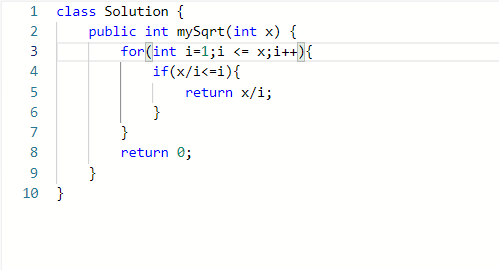
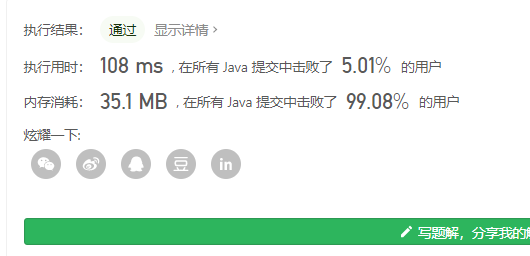
 　　显然，这种笨办法是完全可行的，但是对于大数字要进行多次循环，所以这个代码时间复杂度仍然过高。

 

四、优化与改进思路

　　1、（超出时间限制，弃用）依照题目要求，其实并不需要算出小数位，那么是否可以用比较的方法来优化代码呢？

　　比如说，2^2=4；3^2=9；4^2=16……那么在[4，9）这个区间上的整数开方，按照题目要求就必然为2。（因为不考虑小数）

　　所以按照上述的思路，我们可以对x做一个判断来确定x是属于哪两个整数的平方之间的数。

　　代码思路：

　　　　可以编写一个循环 i为递增变量；循环条件为i<=x;

　　　　循环跳出条件：当i*i>x时返回i-1，当i*i=x时返回i

　　

 

 　　

 

 

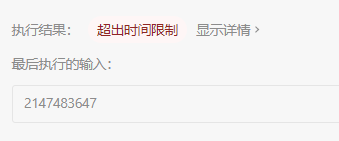
　　但是这种思路也不行，执行上述案例时需要循环四万次。

 

　　2、二分法

　　　　以100为例，求100的平方根其实就是要在1—100中找出一个整数i，使i*i = 100，或者i*i<100且(i+1)*(i+1)>100;

　　　　那么符合上述的i就是要求的平方根。所以可以尝试数据结构中的二分查找法。

　　代码过程；为减少循环次数单独运算0和1，这种情况比较特殊，因为x/2=0，计算起来麻烦

　　　　　　定义一个整型变量mid=x/2。上界max=mid和下界min=0，返回结果rin

　　　　　　循环过程：1、初始化mid=min+（max-min）/2；

　　　　　　　　　　　2、如果mid*mid<=x；rin=mid；移动下界，min=mid+1；

　　　　　　　　　　　3、否则移动上界，max=mid-1；

 

　　　　　　循环结束返回rin即可

　　　

 

 　　

 

 

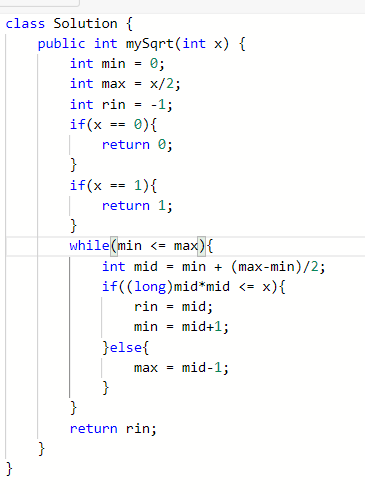
 　　此部分代码参照了leetcode官方代码，也可以看数据结构教材上的二分查找法。

五、总结

　　本题官方给出的解法还有牛顿迭代法，具体可以看leetcode官方题解。就是设函数f(x)=x^2-C，C为待求数值，而该函数的零点就是这个C的平方根

　　牛顿法对我来说只需要了解即可，而关键在于二分查找法的理解。