BUAA_OO_第一单元总结

BUAA_OO_第一单元总结

第一单元作业涉及的内容主要是函数求导，经过三次迭代后能够实现对多项式和三角函数的加法乘法和嵌套求导。

第一次作业

第一次作业为多项式函数的求导，涉及到了乘法和加法求导。

基于度量的程序结构分析

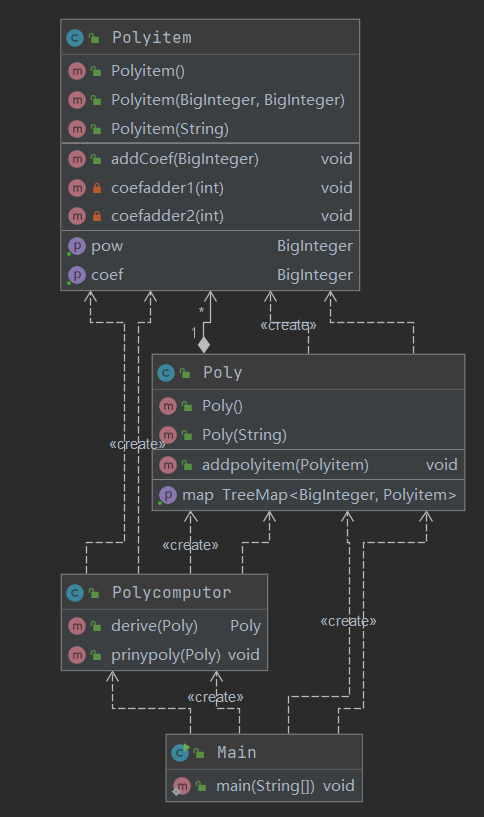
• 架构

  本次作业一共有四个类，分别是主函数类，多项式类，多项式因子类，以及多项式操作类。主函数类读取输入，创建表达式并输出结果；多项式类创建多项式因子，使用TreeMap存储多项式因子并且完成了合并多项式因子的工作；多项式因子类存储了单个因子的指数和系数；多项式计算类实现了打印多项式以及多项式求导的功能。

• 函数调用分析

  在本次作业中没有很好的运用继承的思想，这也是下一次作业进行重构的原因。主函数类调用多项式类根据读取生成一个新的多项式，在调用多项式计算类中的求导生成一个新的多项式类，最后调用多项式计算类中的打印多项式将多项式打印到屏幕上。本次作业虽然实现了每个类干自己的事情，但是由于没有利用好继承的思想，在实现求导和打印的时候需要建立一个新的类，十分麻烦。
  
  
  
  
  

  

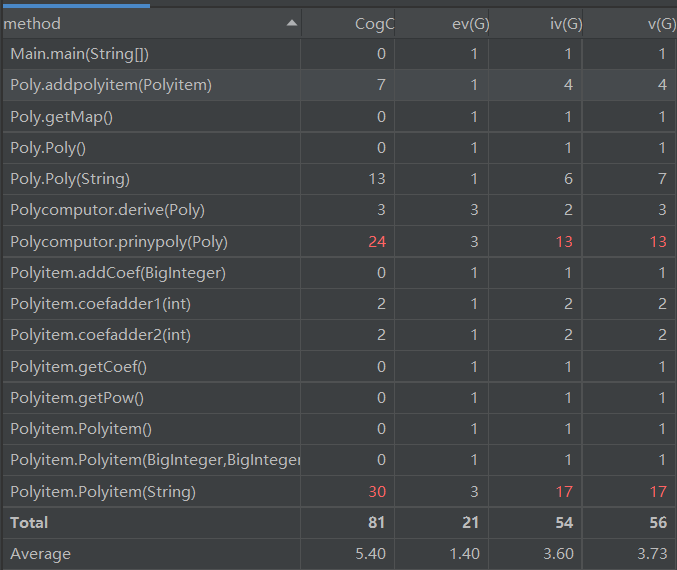
• 复杂度分析

  可以看出虽然每个模块的结构化程度较高，debug较为容易。但是多项式计算函数中的打印多项式与多项式类耦合较高，并且复杂程度高，如果属于多项式类并拆分成更小的方法会是更好的选择；多项式因子类的创建函数的复杂度也较高，并且过多调用了标准模块，应该要将他拆分成更小的方法。

  从上面可以看出，由于是第一次作业，对面向对象编程的思想的运用并不熟练，没有实现具有扩展性的架构。

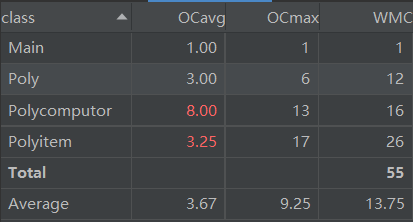
• 代码规模分析

  代码中多项式类和多项式操作类以及Main类的规模适中，但是多项式的项类规模稍大，原因是在这个类里面进行了项的识别与合并。

测评

在强测中没有发现bug，再互测中被发现了一个bug,原因是匹配多项式因子的正则表达式写的过于复杂，在因子相乘数目过多时由于正则表达式的状态机匹配机制会发成栈溢出，在修改了正则表达式之后避免了这样的问题。

在互测中没有发现其他同学的bug，也没有使用自动化测试工具。所以数据的强度和覆盖度可能不够。

第二次作业

第二次作业为简单三角函数和多项式函数的求导，涉及到了乘法和加法求导以及简单多项式的嵌套求导。本次作业中第一次使用了自动测评机，并且使用了继承和抽象类的方法。由于本次作业修改后的架构具有可扩展性，在第三次作业中没有出现较大的修改。

基于度量的程序架构分析

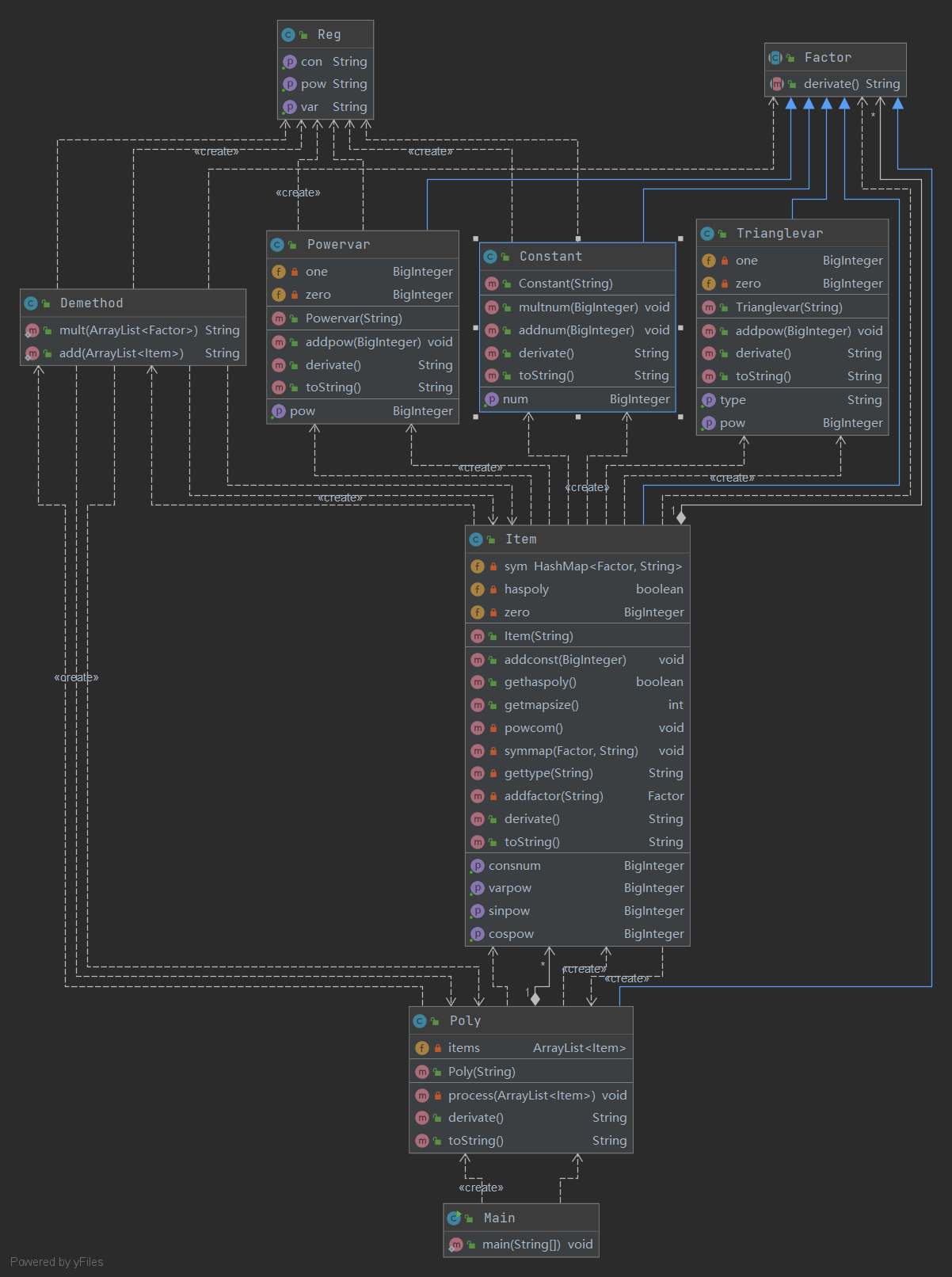
• 架构

  本次作业建立了因子抽象类，常数类，幂函数类以及三角函数类，项类以及多项式类都继承自因子类。其中多项式类存放了项类的容器，项类存放了因子类的容器。并且建立了一个类用于存放使用的正则表达式，以及一个用于实现求导方法的求导方法类，里面含有加法求导以及乘法求导。在主函数中先对输入的多项式字符串进行了预处理，在初始化多项式的过程中用递归下降方法识别每一个项，在项类中用递归下降方法识别每一个因子，完成多项式的创建，再调用求导方法输出结果。

  对于化简，实现了在项类中同类项因子的乘积化简，使用HashMap来存放项的种类以及系数，较为便捷的实现了乘积化简，但是在一定程度上使得程序的复杂度上升了。

• 函数调用分析

  在打印函数以及求导的过程中，实现了主函数类调用多项式类的打印和求导；多项式类调用项类的打印和求导；项类再调用具体因子的打印和求导，通过继承实现了每个类执行自己的功能。

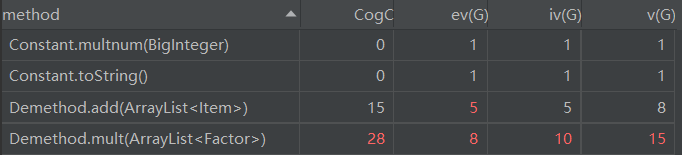
由于本次作业中涉及的方法较多，只对复杂度指标过高的项进行截图和分析，结果如下：

• 复杂度分析

  复杂度较高的地方主要出现在合并同类项，乘法求导以及递归下降识别项或者多项式的地方。除此之外别的类的耦合程度都较低，复杂程度也较低。

  合并同类项复杂度较高是因为这个方法耦合了项类以及常数项类，幂函数类以及三角函数类，但这是合并同类项方法不可避免的，也许可以采用对每个类单独写一个合并同类项方法来实现优化和解耦。而乘法求导的复杂度较高主要是因为在乘法求导的过程中又进行了同类项的合并，由此看出对于合并这一个优化，并没有与其他的设计很好的解耦，应该将合并同类项单独作为一个类抽象出来，作为一个单独的功能实现。而在递归下降识别项和多项式的过程中，由于在判断结束的过程中涉及到了较多的布尔表达式，导致程序的复杂度较高。

  虽然由于优化导致了部分模块的复杂度较高，但是本次作业的架构具有较好的可扩展性。但是由于复杂度较高，导致可能出现的bug较多，不容易找出，这也导致了最后在强测中出现了一个较大的bug。

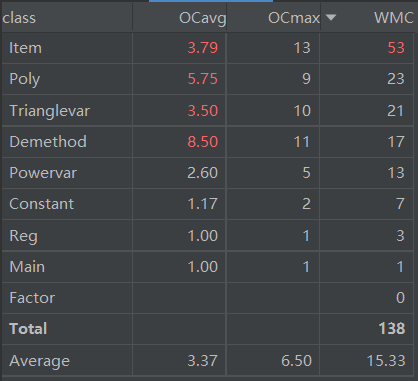
• 代码规模分析

  从上图可以看出每个类的规模都较为均匀，但是项类以及多项式类的规模较大，原因是在这两个类中都进行了递归下降的语法分析，并且在项类中对乘积的同类项进行了合并，在多项式类中也对括号做了优化导致代码量较大。

重构经历总结

本次作业相对于第一次作业进行了重构，通过之前的图片可以看出来，由于使用了继承的方法，不需要单独再写一个求导函数以及打印函数，这带来了很大的便利。但是由于题目复杂度的上升，导致代码的复杂度也上升了。

测评

在强测和互测的过程中都被发现了同一个bug，在多项式求导的时候，判断出现了问题，当求导前乘积因子只有一个时就去掉了括号，导致求导后可能出现多个项的和并且括号以及被去掉的情况。最后通过修改了判断逻辑修复了bug。

在互测中发现了其他同学的bug，在涉及到复合函数求导的时候无法正确处理符号。本次互测采用了自动化测评机，但是由于采用了随机的数据生成，虽然测试了较多的数据，但是数据的覆盖性以及强度仍然不够，还是需要通过手动生成一些较强的数据。

第三次作业

第三次作业实现了嵌套因子的三角函数以及多项式函数的符合求导，涉及到了乘法加法以及嵌套求导法则，并实现了简单的WF的判断。本次作业采用了自动化测评的方式来验证自己的正确性，效果较好。

基于度量的程序架构分析

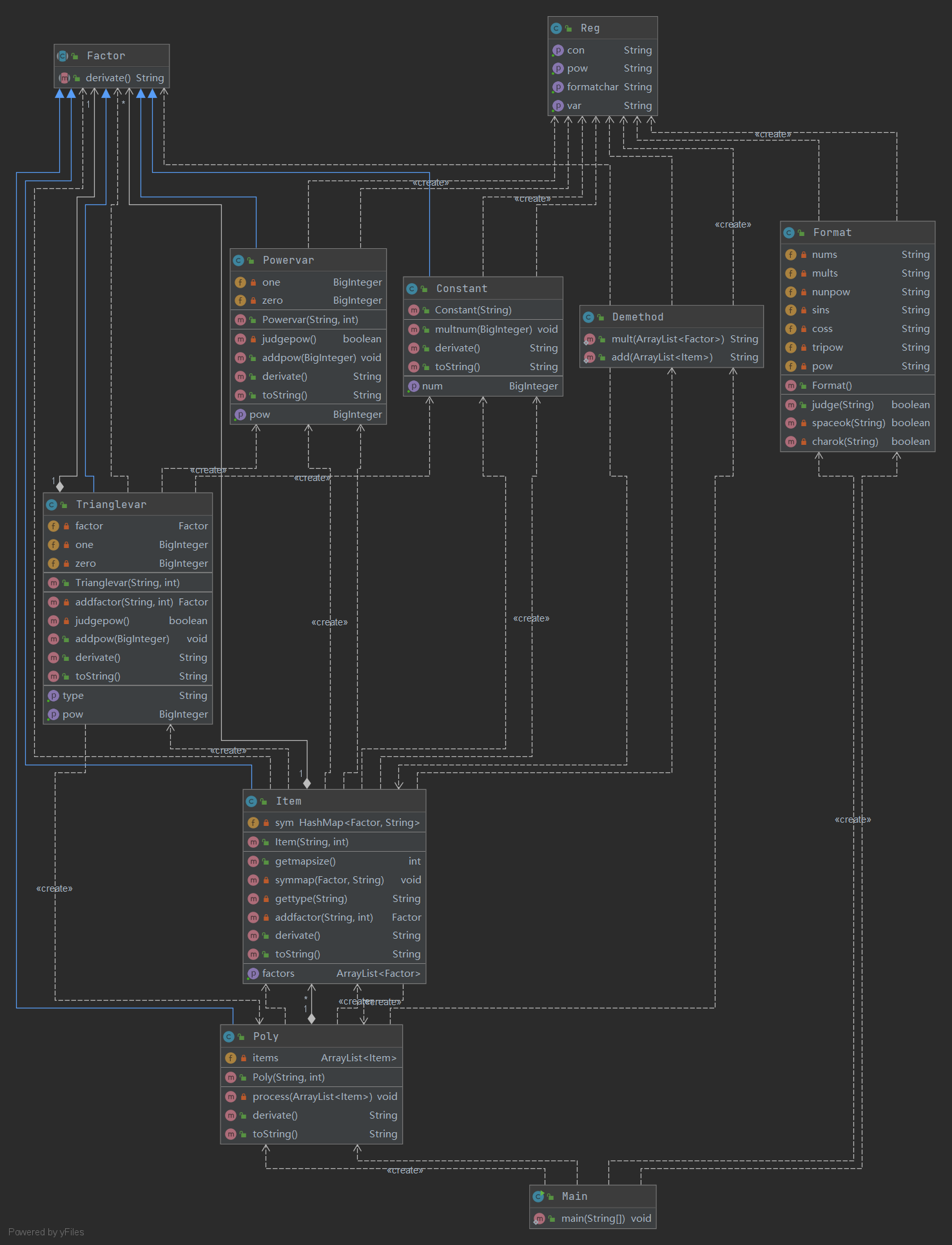
• 架构

  第三次作业的架构和第二次基本上一样，新增了用于判断WF的Format类，以及在三角函数类中增加了因子项，以及在三角函数类，幂函数类中增加了关于指数的判断。并且只有在第一次识别的时候判断指数的合法性，在化简过程中不需要判断指数的合法性。

• 函数调用分析

  基本上和第二次作业一样。在求导和打印的时候都采用了层层递进的思想，实现了每个类解耦程度较高。

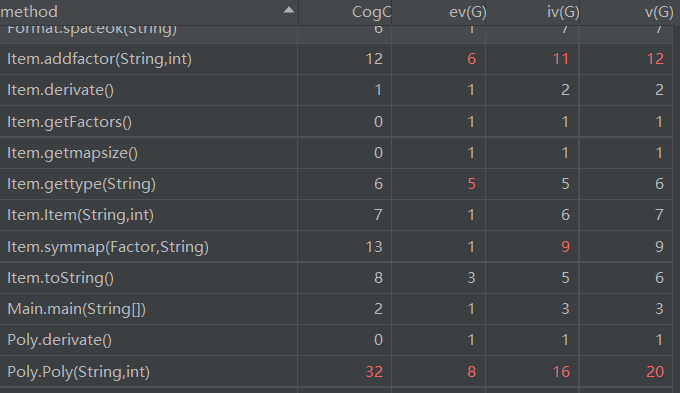
由于本次作业中的方法较多，只对复杂度较高的方法进行分析。

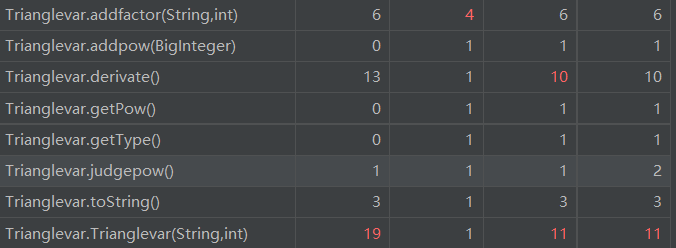
• 复杂度分析

  复杂度较高的地方基本上与第二次作业一样。不同之处是第三次作业优化了乘法求导方法，使得乘法求导方法的复杂度下降以及由于三角函数类新增了因子类导致三角函数类与其他类的耦合程度变高。但是总体来说基本上实现了每个类的分工以及在继承关系上的合作。
  
  
  

• 代码规模分析

  从上图可以看出经过第三次作业的优化之后，每个类的规模都逐渐均匀，没有特别大的类。

测评

在本次测评中，由于对于导函数又建立了一次多项式，导致对于导函数过长的时候可能出现超时问题。在强测中超时了一个点。并且由于类中包含的内容过多，在处理多层嵌套的过程中会出现CPU超时问题，为此修改了对括号的初始化处理，避免了多层嵌套导致的超时。

关于自动测评机的应用，首先是在自己测试的过程中运用了对拍的方法，找到了自己的bug：在判断指数非法的时候是输入的指数而不是化简后的指数。在互测的过程中也发现了其他同学的两个bug：对于(00)无法处理，对x**0无法处理。

发现别人bug所采用的策略

静态观察代码

有些同学的bug在于对因子或者项的求导方法书写遗漏了部分情况或者对部分情况的处理有误，这种bug可以通过静态观察代码来找到。

手动生成测试用例

有些同学的bug出现在处理边界数据的时候，包括本人自己。可以手动生成一些特征较强的边界数据，比如多个因子乘积，多个三角函数嵌套，多个多项式因子嵌套，一些较大的整数系数，以及枚举所有的WF情况等。这些针对性较强的数据如果仅仅通过随机生成数据很难得到，最好是自己手动生成再拿来测试。

自动生成测试用例并对拍

有些同学的bug出现再基本的正确性上，这种时候可以通过随机生成的测试数据来对拍寻找bug。由于自动生成的随机数据通常长度较大，在寻找bug的过程中需要去找到出现bug的最短长度，做到精准定位bug。

心得体会

• 架构很重要。一个扩展性良好的架构能够帮助自己节省大量的时间，在写代码之前应该花更多的时间思考自己的架构以及自己架构的扩展性。
• 代码的逻辑应该更加清晰，语句应该更加简单。用过多的复杂语句以及复杂逻辑不仅不利于自己阅读，并且容易产生大量难以发现的bug。
• 多和其他人讨论交流，学习别人的架构的长处，完善自己的架构。比如在第一次作业中就有同学使用了递归下降的方式来处理输入，会对后面的作业带来很大的方便。
• 在通过中测之后仍然需要对自己的代码进行测试和优化，只有覆盖性强的测试才能产生一份正确性较高的代码。