大杂烩
-
平台:IA-64 + linux + C + gcc
-
检测引用错误的工具(例如 Valgrind)
-
在 linux 系统中:gdb
在 Macintosh OS 上:lldb -
很多开源库都用 size_t 类型的循环计数器
-
操作系统:管理进程状态
-
系统为每个 进程 提供私有地址空间
-
编译
-
预处理程序
-
处理 #include 指令(包含头文件)
-
处理 #define 指令(宏定义替换)
-
处理条件编译 #if, #ifdef
- 输入:.c 或 .cpp 源文件
输出:预处理后的源文件(.i)
-
-
编译器:将预处理后的源代码翻译成 汇编代码
- 输入:预处理后的源文件 (.i)
输出:汇编代码文件(.s)
- 输入:预处理后的源文件 (.i)
-
汇编器:将汇编代码转换成 机器码
-
输入:汇编代码文件 (.s)
输出:目标文件(.o 或 .obj) -
缺少不同文件间代码的链接信息
-
-
链接器:将多个目标文件和库文件连接成最终的 可执行文件
-
输入:一个或多个目标文件 (.o) + 库文件
输出:可执行文件(在 Windows 是 .exe,Linux 无扩展名) -
解析不同文件之间的 引用关系
与静态运行时库 合并
(例如 malloc、printf 的代码)
部分库采用 动态链接
链接过程在程序开始执行时进行
-
-
-
反汇编器
-
volatile 告诉编译器
-
这个变量可能被意外修改
(比如硬件、其他线程、或越界写) -
所以不要对它做优化
(比如缓存到寄存器、重排读写顺序) -
必须严格从内存中读写它的值
-
-
异常控制流
-
程序正常的执行流程被中断或改变
-
包括硬件中断、系统调用、进程切换等
-
信号是其中一种软件层面的实现方式
-
信号是操作系统提供的一种 进程间通信机制
用于通知进程发生了某个事件 -
异步发生:信号可以在程序执行的任何时刻到达
-
软件实现:由操作系统内核管理和传递
-
改变控制流:当信号到达时,程序会暂停当前执行,跳转到信号处理函数
-
-
固定转移
远距离转移
-
存储
-
存储器
硬件,高速缓冲存储器,dram 的层次结构 -
dram
-
计算机、服务器的主内存,显卡的显存
-
主存储器 主要由 DRAM(动态随机存取存储器)构成
-
-
ddr
-
通信标准/协议
-
规定了 内存控制器(通常在CPU内)如何与 DRAM芯片 对话
即如何传输 数据、地址和控制命令 -
在每个时钟周期的 上升沿和下降沿 都传输一次数据
-
-
cpu
-
PC(程序计数器)
存储 下一条要执行的指令 的地址
在 x86-64 架构中,被称为 RIP -
寄存器组
用于存储程序中频繁使用的数据 -
条件码
存储最近一次算术或逻辑操作的状态信息
为条件分支(如 if 判断、循环)提供依据
-
-
内存
-
内核空间(高地址):操作系统内核专属区域,隔离用户程序
-
栈区:向下增长(高位地址 向 低位地址 扩展)
-
内存映射区:用于共享库、mmap 分配等动态区域
-
堆区:向上增长(低位地址 向 高位地址 扩展)
-
bss段:存储未初始化的全局 / 静态变量
-
数据段:存储初始化的全局 / 静态变量
-
rodata段:存储只读数据(如字符串字面量)
-
代码段(低地址):存储程序指令
-
-
内存 和 cpu
-
CPU 向 内存 发送 地址
-
内存 向 CPU 传输 指令
-
数据在 CPU 和 内存 之间双向传输
-
-
内存和磁盘
-
程序启动:磁盘→内存(加载数据)
-
磁盘先将程序的
可执行文件(如 word.exe)
文档的原始数据(如报告.docx)
读取到内存 -
CPU只能直接访问内存
(无法直接读取磁盘数据) -
CPU直接 从内存访问指令和数据
-
内存速度远快于磁盘
加载到内存后
程序才能快速响应操作
(如打字、排版)
-
-
运行中:内存→磁盘(保存数据)
-
程序运行时产生的 临时数据
会先 存放在内存 中-
如正在输入的文字
未保存的修改 -
速度快,适合实时交互
-
-
保存时
内存会将这些临时数据 写入磁盘
转为 永久存储
(即使断电,磁盘中的数据也不会丢失) -
若未保存就断电
内存中的临时数据会 丢失
(内存易失性)
但磁盘中之前保存的版本仍存在
-
-
空间不足:磁盘→内存(扩展缓存)
-
当内存容量不够时
(如同时开太多软件)
系统会启用 “虚拟内存” 技术 -
从 磁盘中划分 一块空间
当作 临时内存 使用- 如 Windows 的 页面文件
Linux 的 交换分区
- 如 Windows 的 页面文件
-
内存管理单元(MMU)负责地址转换
页面交换(Paging):将不常用的内存页 换出到磁盘 -
速度变慢,因为磁盘远慢于内存
-
-
常见性能问题
-
内存不足 → 频繁的磁盘交换 → 系统变慢
-
磁盘I/O慢 → 程序加载和数据访问延迟
-
内存与磁盘速度不匹配 → 整体性能受限
-
-
优化策略
-
增加内存:减少 磁盘交换频率
-
使用SSD:提高 磁盘访问速度
-
优化数据布局:提高 缓存命中率
-
预读取技术:提前将可能需要的数据 加载到内存
-
-
数据库工作流程
-
数据页从磁盘加载到内存缓存池
-
查询在内存中执行
-
事务提交时,脏页异步写回磁盘
-
日志机制确保数据一致性
-
-
操作系统调度
-
进程创建:程序代码从磁盘加载到内存
-
上下文切换:进程状态在内存中保存和恢复
-
文件缓存:常用文件数据缓存在内存中
-
-
-
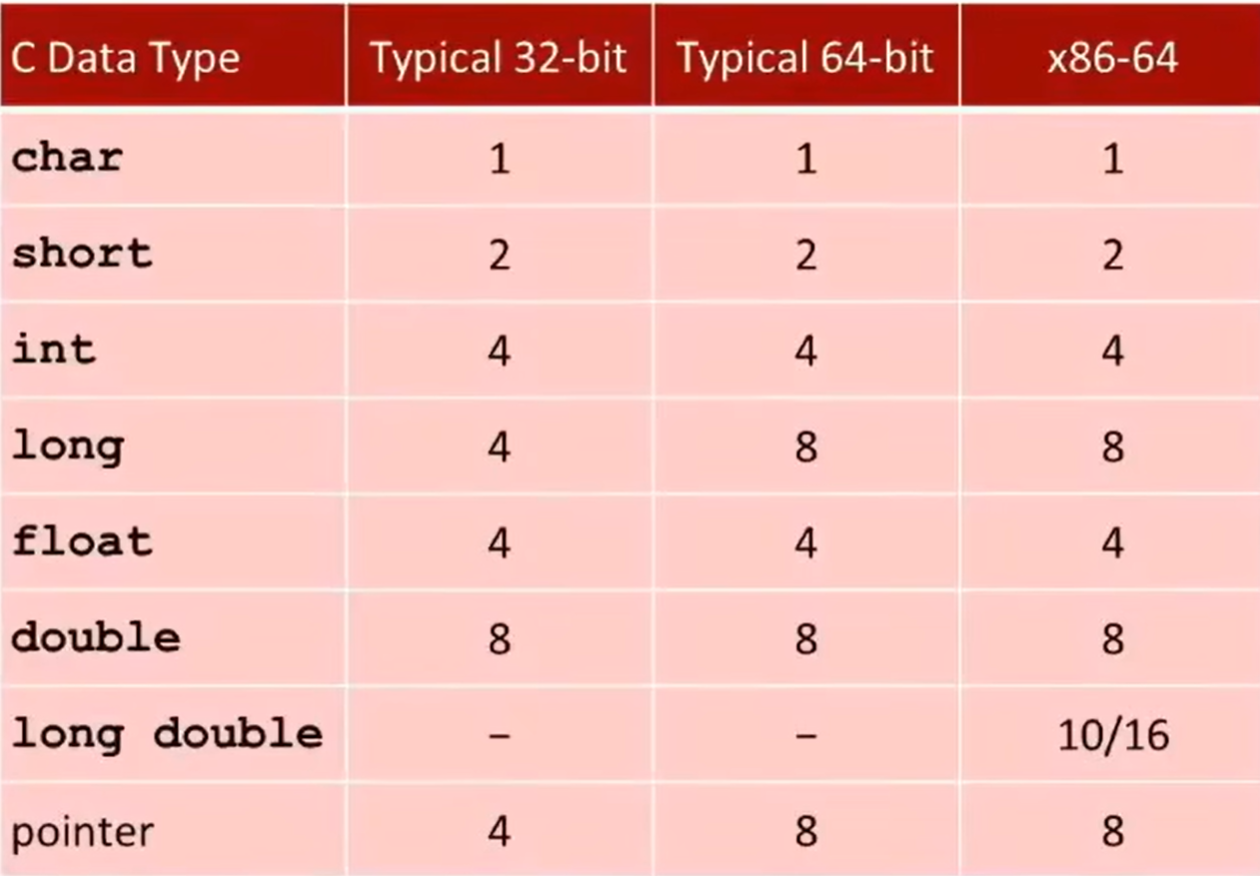
数据类型,大小
![image]()
-
在 x86-64 架构中
long double 的实际有效数据长度是
10 字节(80 位扩展精度) -
但由于内存对齐要求
编译器会将其存储为
16 字节(128 位) -
这中间的 6 字节属于 “填充” 空间
-
SIMD指令支持
现代CPU的向量寄存器通常是16字节的倍数
16字节对齐便于使用SSE/AVX指令 -
缓存行优化
缓存行通常为64字节
规整的大小便于缓存管理 -
现代处理器的内存控制器和缓存系统
以 16 字节为基本读写单元
(尤其是支持 SSE/AVX 指令的处理器)
如果数据未对齐
CPU 需要多次访问内存并手动拼接数据
导致性能大幅下降
-
-
字与字节
-
内存的 最小寻址单位是 字节
-
每个字节 都有唯一的地址
-
字是比字节更大的存储单位
通常为 32 位或 64 位
一个字 包含多个字节 -
对于32 位字(占 4 字节),下一个字的地址比前一个字的地址大 4
对于64 位字(占 8 字节),下一个字的地址比前一个字的地址大 8
-
-
struct 内存对齐
-
成员对齐
-
结构体中每个成员的起始地址
必须是其自身大小的整数倍 -
若不满足,编译器会在成员之间插入填充字节
-
-
整体对齐
-
结构体的总大小必须是其最大成员大小的整数倍
-
若不满足,编译器会在结构体末尾插入填充字节
-
-
-
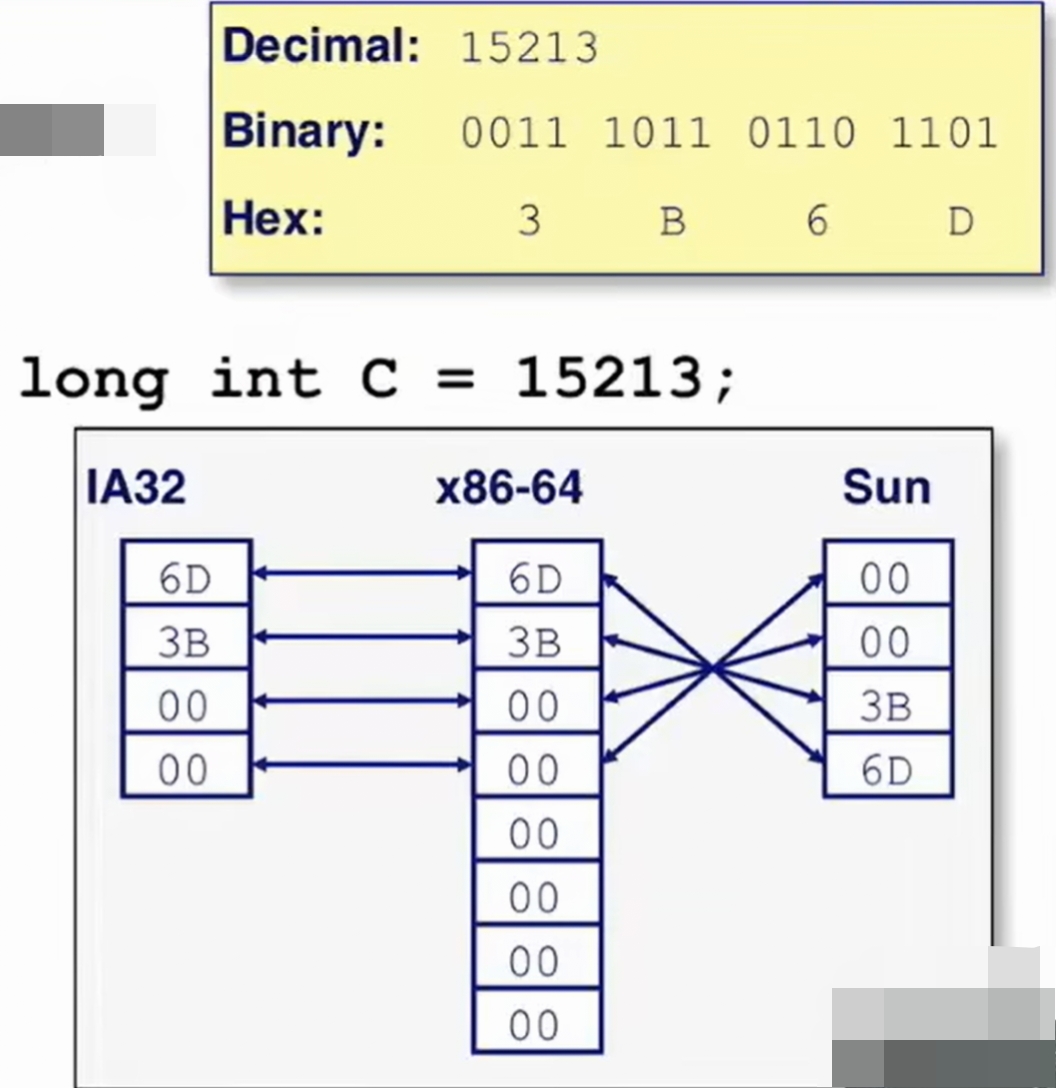
大端序(高位字节存低地址)
小端序(低位字节存低地址)-
大端序:可读性好,符合直觉
小端序:机器性能好,处理更快 -
x86 架构通常是小端序
-
所有网络数据包中的 32 位字
必须以大端序传输-
大端序将关键信息(如 IP 地址、端口号)的高位字节
置于数据包起始位置
接收方无需额外转换即可直接读取
解析效率更高 -
IPv4 头部的 协议类型 字段(1 字节)
TCP 头部的 源端口 字段(2 字节)
均按大端序排列
-
uint32_t value = 0x12345678; // 大端序 (网络字节序) 内存地址: 低地址 -> 高地址 字节顺序: 0x12 0x34 0x56 0x78 // 小端序 (x86/x64主机字节序) 内存地址: 低地址 -> 高地址 字节顺序: 0x78 0x56 0x34 0x12![006f322ca40fd8e936dab5082eba8186]()
-
ASCII 字符是 单字节编码
字符串由 “逐个单字节字符” 组成 -
多字节数据(如 int、double)
会受 “大端 / 小端” 字节序影响 -
单字节的字符不存在 “字节序反转” 问题
-
-
缓存 Cache
-
速度远快于主存(如 DDR 内存)
-
容量较小
-
没有操作缓存的指令
无法直接访问缓存 -
命中
CPU 访问数据时
若缓存中已存在该数据
直接从缓存读取 -
失效 / 缺失
缓存中无该数据
需从主存加载数据到缓存- 需等待主存响应
性能下降
- 需等待主存响应
-
缓存行 Cache Line
-
缓存 与 主存 的数据交换单位
通常大小为 64 字节 -
缓存由 缓存行 组成
-
若 CPU 需要当从主内存中读取数据时
不仅会读取请求的数据
还会将其附近的数据一起 读入缓存行- 相邻内存地址 的数据
会被一起加载到 缓存
- 相邻内存地址 的数据
-
-
多级缓存
-
l1
-
分为 指令缓存(I-Cache) 和 数据缓存(D-Cache)
-
优先存储最常用的指令 / 数据
-
CPU 内核内
-
每个核心独有
-
-
l2
-
比 L1 慢,但更大
-
缓存 L1 未命中的数据
-
CPU 内核外
-
每个核心独有
-
-
l3
-
比 L2 慢,但更大
-
缓存 L2 未命中的数据
-
所有核心共享
-
![4853474114b63c06f6ce4cc0d8ab944c]()
-
-
组织结构
-
直接映射:每个主存块 只能映射到缓存中的 一个特定位置
-
内存块地址 MOD 缓存中的总行数
-
硬件简单,查找速度快
-
冲突率高
如果两个频繁访问的内存块恰好映射到同一个缓存行
它们会不断地相互驱逐
导致 缓存抖动
性能急剧下降
-
-
全相联:每个主存块 可以映射到缓存中的 任意位置
-
冲突率最低
缓存空间的利用最充分 -
硬件复杂,速度慢
-
-
组相联:每个主存块 可以映射到缓存中的 一组中的任意一个位置
-
组的选择:内存块地址 MOD 组数
-
组内全相联
- 若组内已满,则通过替换算法(如 LRU)在组内选择一个缓存块替换
-
N 路组相联:每组包含的行数 N
-
- 小容量缓存(如TLB)采用 全相联
x86 采用 组相联
-
-
加载 新数据,淘汰 旧数据
- 缓存容量不足时
-
LRU:淘汰 “最近最少使用” 的数据
-
FIFO(先进先出):淘汰 最早进入缓存 的数据
-
随机淘汰
- 性能较差但实现简单
-
缓存数据的写入
- 当 CPU 修改 缓存 中的数据时
需同步更新 主存
-
写直达:写缓存的同时立即写主存
- 数据一致性强
- 速度慢
-
写回:仅写缓存,当该数据被 淘汰 时再写回主存
- 速度快
- 需 脏位 标记是否修改过
- 当 CPU 修改 缓存 中的数据时
-
多核
需处理 缓存一致性 问题
(如 MESI 协议)
避免不同核心缓存数据冲突![image]()
-
行优先
有利于缓存性能
因为CPU缓存可以预取连续的内存块
减少缓存缺失 -
如果程序访问的内存地址连续 / 邻近
缓存命中率高
能大幅减少慢内存的访问次数
提升效率
-
-
缓存和虚拟内存的效应会极大地影响程序性能
-
虚拟地址空间由机器字长决定
32位机,地址是 4 字节
64位机,地址是 8 字节-
64 位机的 “64 位” 核心指
数据总线 / 地址总线宽度 -
64 位 CPU(如 x86-64、ARMv8-A 架构)
的算术逻辑单元(ALU)
原生支持 64 位数据运算 -
x86-64架构
通常使用48位虚拟地址空间
用户空间通常使用47位有效地址
最高位用于区分 用户/内核 空间 -
地址的规范形式
低 48 位(位 0~位 47)作为有效地址位
高 16 位(位 48~位 63)必须是位 47 的 “符号扩展”
(即高 16 位与位 47 的值完全一致) -
地址空间划分
// 典型的x86-64虚拟地址布局 用户空间: 0x0000000000000000 - 0x00007FFFFFFFFFFF // 47位有效 内核空间: 0xFFFF800000000000 - 0xFFFFFFFFFFFFFFFF // 47位有效-
内存的最小寻址单位是 字节,每个字节都有唯一的地址
-
gcc 可以指定64位编译或32位编译
-
64 位系统环境下
GCC 默认会编译生成 64 位程序 -
若要生成 32 位程序
需使用 -m32 选项
但前提是系统已安装 32 位编译工具链
(如 Linux 需安装 gcc-multilib 包
Windows 下 MinGW 需配置 32 位工具链)
-
-
整数
-
集合的表示
- 位向量 01101001 表示集合
-
逻辑运算支持 提前终止(短路求值)
-
移位
- 左移
丢弃左侧溢出的额外位
右侧用 0 填充
-
逻辑右移
丢弃右侧溢出的额外位
左侧用 0 填充 -
算术右移
丢弃右侧溢出的额外位
左侧复制最高有效位(符号位) -
CPU中移位指令
位移量要小于被位移数的位数
比如左移数A(假设8bit)
A << 10
左移的位数大于数本身的位数
10 mod 8 = 2
即左移2位 -
在 x86 架构中:
SHL reg, cl 指令
实际使用的是 CL 寄存器的低 n 位
n 取决于寄存器宽度:-
8 位寄存器:取 CL & 0x07(mod 8)
16 位寄存器:取 CL & 0x0F(mod 16)
32 位寄存器:取 CL & 0x1F(mod 32)
64 位寄存器:取 CL & 0x3F(mod 64) -
在汇编里写 mov al, 1; shl al, 10
实际上会左移 10 mod 8 = 2 位
-
- 左移
-
数字的表示
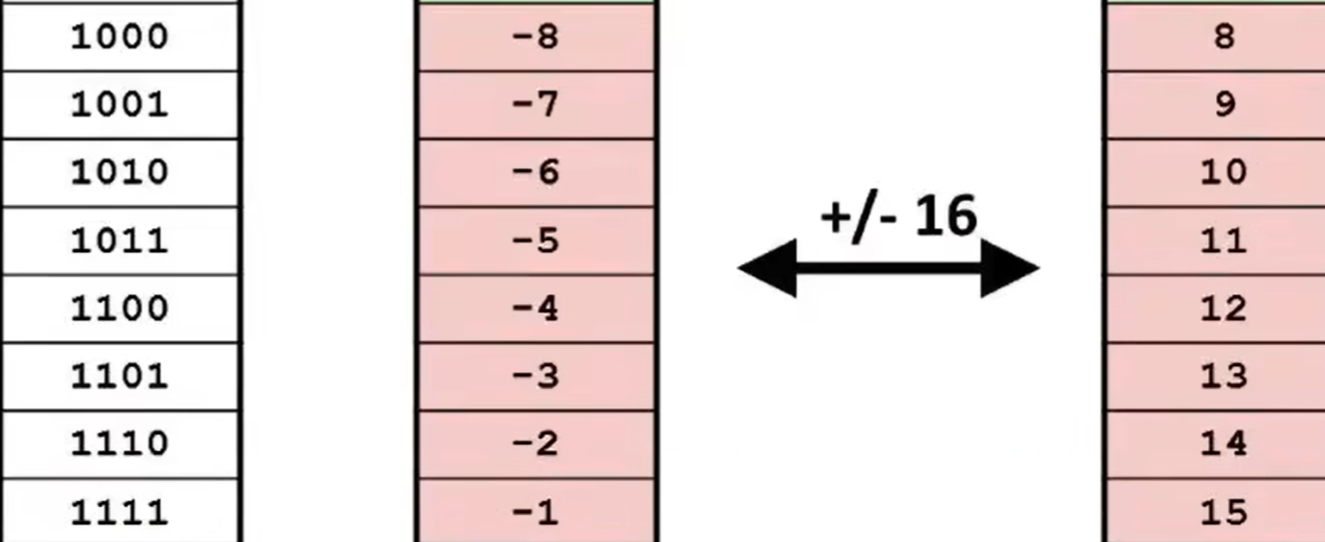
- 按位取反运算符 ~
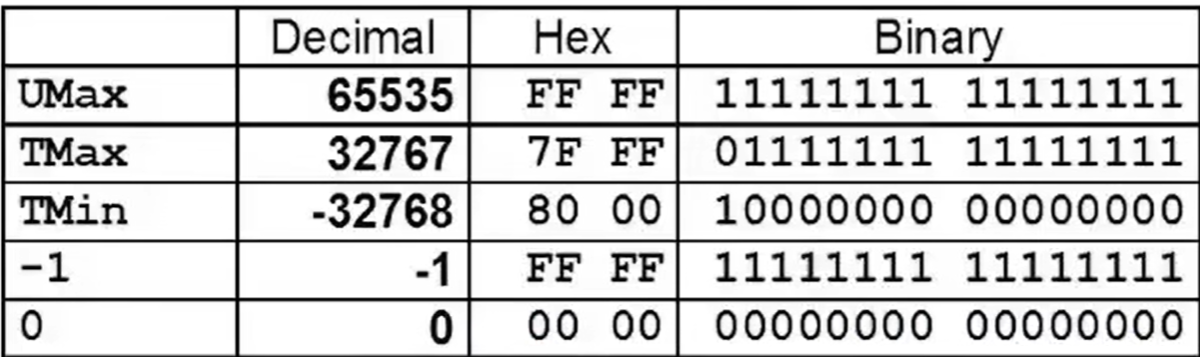
- 有符号整数:补码(5 变成 -6,127 变成 -128)
- 无符号整数:最大无符号值 − 原值
![image]()
TMAX 与 TMin 互为补码
∣TMin∣ = TMax + 1
UMax = 2 × TMax + 1
(左移一位,右侧补零,加 1 把右侧的 0 变为 1)
![image]()
有符号数 ←→ 无符号数
![image]()
死循环
无符号数永远 不会小于 0for (size_t i = n; i >= 0; --i){ func(arr[i]); }无符号数作为索引
for (size_t i = cnt - 2; i < cnt; --i) a[i] += a[i+1]; -
当一个表达式中混合了 有符号和无符号 类型时
有符号值会隐式转换为 无符号值
再进行 运算 或 比较 -
符号扩展
有符号整数:w 位 → w + k 位
复制 k 次符号位 -
截断
-
都是丢弃高位,保留低位
无符号:x mod 2 ^ k,k 为要保留的位数
有符号:结果会被重新解释为有符号值,可能出现 正变负,负变正 -
无符号整数加法
计算机硬件存储无符号数时
位宽固定为 w
最终结果是 (u + v) mod 2^w
数学加法 + 可能加上或减去 2^w -
有符号整数加法
数学加法 + 可能加上或减去 2^w-
正溢出:若和 ≥ 2^(w-1)
(4 位下为 ≥ 8)
结果会变成负数 -
负溢出:若和 < -2^(w-1)
(4 位下为 < -8)
结果会变成正数
-
-
无符号整数乘法
u 和 v 都是 w 位
结果为 uv mod 2 ^ w -
整数除法
向 0 取整
-
-
整数乘法与移位
编译器 可能会解释为移位
当乘数是 2 的幂 时,乘法可被等价转换为左移 -
求相反数
取反加一
简单证明:x + ~x = 111....111 = -1-
x 和 y 都是 int 类型的
已知 x > y
不能得出 -x < -y -
特例
int a = -2147483648; assert(a == -a); -
-
掩码
二进制数,按位与
筛选 出目标数据的 特定位
限制 数值范围-
非负整数 n
n & 7 == n % 8
按位与 远快于 取模 -
需要保留的位,则和 1 相与
需要清除的位,则和 0 相与
-
浮点数
-
![image]()
-
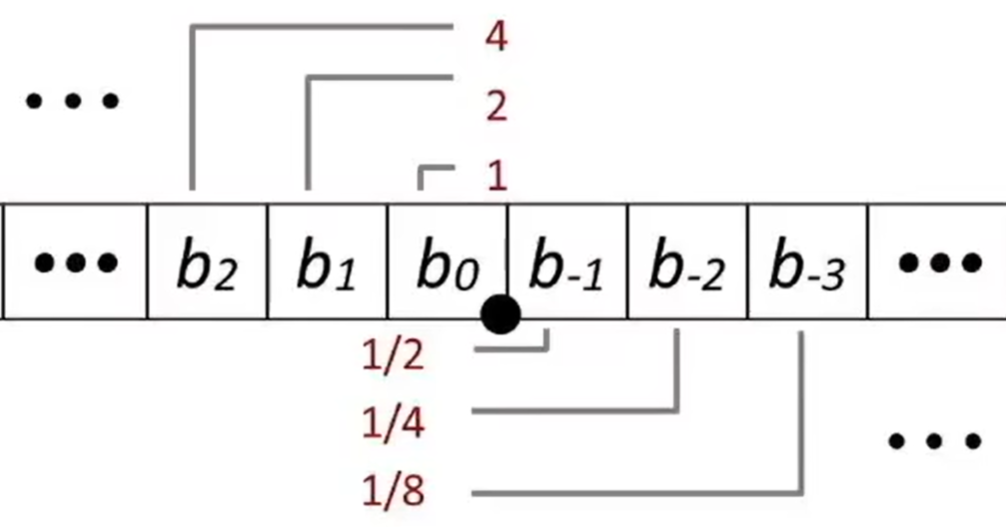
计算机只能精确表示
形如 x / (2 ^ k) 的数
x 是整数,k 是正整数 -
十进制小数:乘以 2^n
其二进制表示:小数点右移 n 位 -
定点数:小数点位置固定
浮点数:阶码范围有限 -
若要表示极小数,如 10^(-300)
可能因位数不足 下溢 为 0
若要表示极大数,如 10^300
可能因位数不足 上溢 为无穷大 -
浮点数的数学表达式
二进制的科学计数法
![image]()
-
符号位 s
-
有效数 M
通常是规范化的小数
范围在 [1.0, 2.0) 之间 -
指数 E
范围是 - 126 到 + 127 (单精度)
范围是 - 1022 到 + 1023 (双精度)
-
-
编码
![image]()
-
浮点数通过三个二进制字段存储
-
符号位 s
-
指数字段 exp
-
小数字段 frac
- 只存储 M 的小数部分
![image]()
-
-
double (8 字节 64 位)
1 位 s
11 位 exp
52 位 frac
d7 ... d4:高 4 字节(对应浮点数的高位部分,如 exp 和 frac 的高位)
d3 ... d0:低 4 字节(对应浮点数的低位部分,如 frac 的低位) -
float(4 字节 32 位)
1 位 s
8 位 exp
23 位 frac -
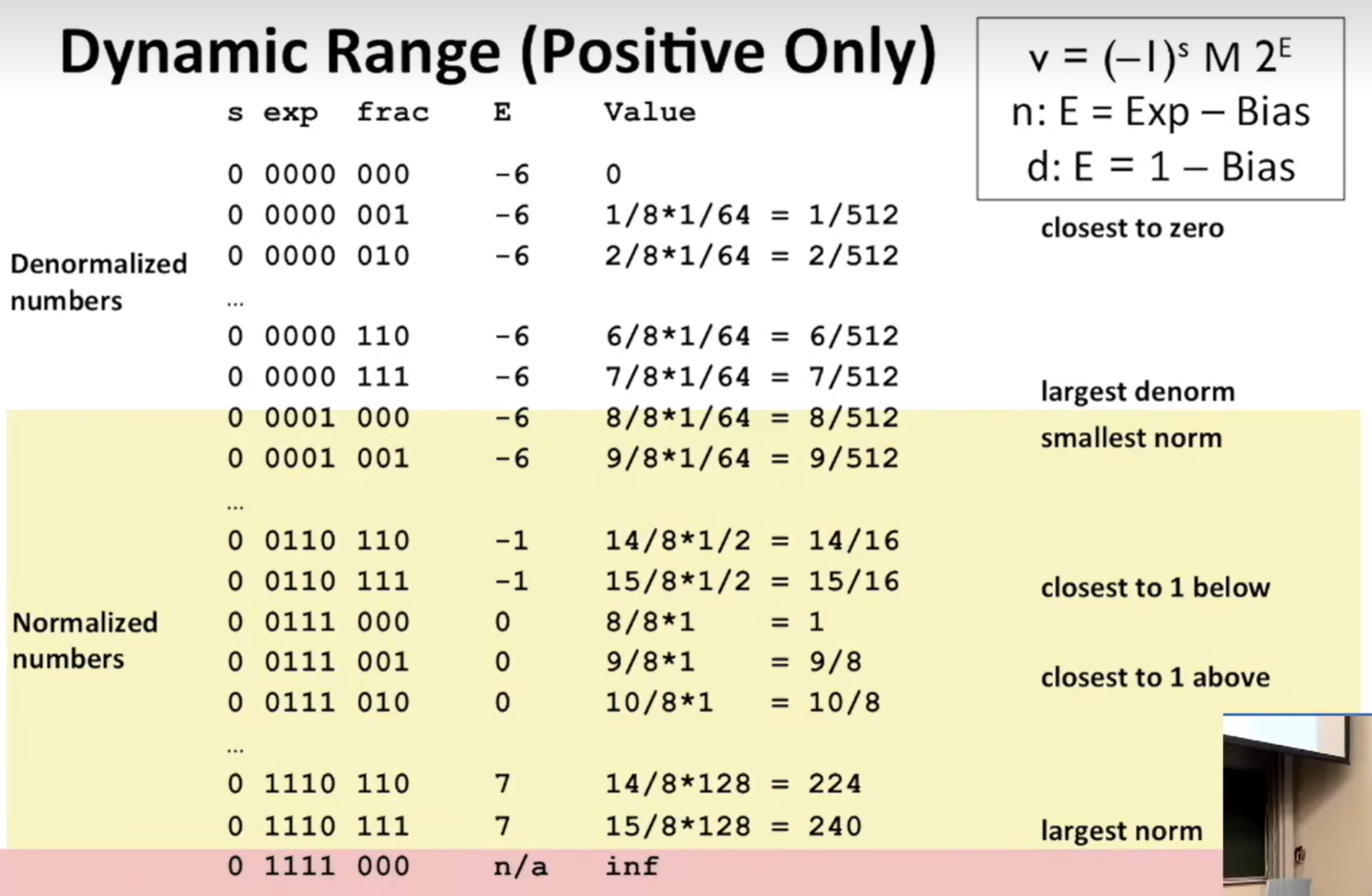
规格化值
-
exp 的所有位的值
既不能 全是 0
也不能 全是 1 -
exp = E + 固定偏置量
-
用 无符号数 来同时表示 正、负指数
-
单精度中,8 位指数字段的偏置量为 127
双精度中,11 位指数字段的偏置量为 1023 -
单精度中,exp 的范围: 1 到 254
双精度中,exp 的范围: 1 到 2046
-
-
-
非规格化值
-
exp 为全 0
-
exp = E + 固定偏移值 ❌
1 = E + 固定偏移值 ✔-
非规格化数的 E 为 -126(单精度)
和规格化数的 E 的最小值相等 -
最大的非规格化数(frac全 1 时)
刚好小于 最小的规格化数 -
保证了数值从 0 到最小规格化数的 连续性
-
-
规格化数, M 整数部分为 1
非规格化数,M 整数部分为 0 -
若 exp = 000…… 且 frac = 000……:表示零值。
- 注意存在不同取值:+0 和 -0
-
若 exp = 000…… 且 frac ≠ 000……:表示最接近 0.0 的数
- 这些数是等间距的
-
-
特殊值
-
exp 全为 1
-
若 exp = 111…… 且 frac = 000……:∞
-
包含正无穷和负无穷
-
1.0 / 0.0 = -1.0 / -0.0 = +∞
-
1.0 / -0.0 = -∞
-
-
若 exp = 111…… 且 frac ≠ 000……:NaN(非数)
- √-1,∞ - ∞,∞ × 0
-
-
示例
![image]()
-
0 附近精度更高
-
小值密集、大值稀疏
-
-
舍入模式
-
向零舍入
-
向下舍入,朝向负无穷
-
向上舍入,朝向正无穷
-
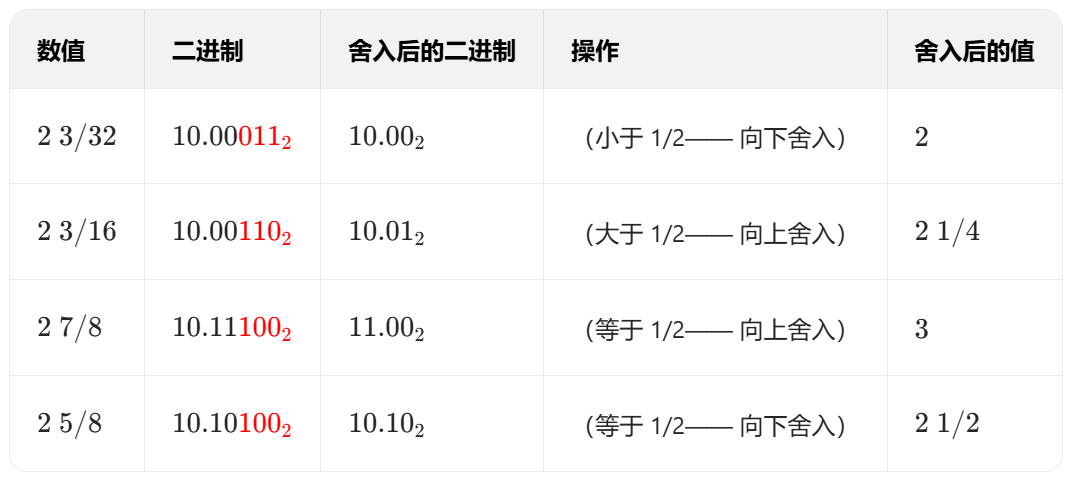
四舍六入五凑偶
-
IEEE 浮点数的默认舍入模式
-
平衡舍入偏差,让误差更均匀
-
偶:最低有效位为 0
-
五:舍入位置右侧的位为 100……
![image]()
-
-
-
浮点数的加法的性质(对比 阿贝尔群)
-
对加法封闭
- 但可能产生 ∞ 或 NaN
-
可交换,但不满足 结合律
- 溢出与舍入的不精确性
-
每个元素都有加法逆元
- 无穷大和 NaN 除外
-
若 a >= b,则 a + c >= b + c
- ∞ 和 NaN 除外
-
-
浮点数乘法的性质(对比 交换环)
-
对乘法封闭
- 但可能产生 ∞ 或 NaN
-
可交换,但不满足 结合律
-
乘法单位元是 1
-
乘法对加法 不满足 分配律
-
若 a >= b 且 c >= 0,则 a × c >= b × c
- ∞ 和 NaN 除外
-
-
浮点数加法(数学表达式)
-
小数点对齐,使指数匹配
-
E 大的数不动
-
E 小的数,M 的小数点右移 k 位
- k 为两个数的 E 的差的绝对值
-
-
符号处理与相加
-
s 不同
-
s' 与 M 较大的数 的 s 相同
-
M' = 两个 M 的差的绝对值
-
-
s 相同,E 相加
-
-
规格化
-
若 M > 2
-
有效数溢出一位
-
M 的小数点左移一位
-
E 加 1
-
-
若 M < 1
-
M 的小数点右移 k 位,直到 1 <= M < 2
-
E 减 k
-
-
-
-
浮点数乘法(数学表达式)
-
精确结果
-
s = s1 异或 s2
-
M = M1 × M2
-
E = E1 + E2
-
-
调整
-
若 M > 2,将 M 右移,并对 E 加 1
-
若 E 超出范围,发生溢出
-
对 M 舍入,以适配 frac 的精度
-
-
浮点数与整数
-
int, float, double 类型转换
-
double/float 转换为 int
- 截断小数部分
绝对值变小
类似于 向零舍入
- 截断小数部分
-
int 转换为 double
- 不会有精度损失
-
int 转换为 float
- 当整数的 绝对值 大于 2 ^ 24 时
转换会有精度损失- 因为 float 的 frac 23位
- 当整数的 绝对值 大于 2 ^ 24 时
-
-
x² >= 0
-
x 是 float 类型
x 为 NaN 时 ❌
其他情况 ✔ -
x 是 int 类型
是整数模环
-2的31次方 到 2的31次方-1
可能会溢出
-
-
(x + y) + z == x + (y + z)
-
int 或 unsigned int
正确
为什么 -
float 类型
float a = 1e20; float b = 3.14; cout << (a - a) + b << endl; cout << a + (-a + b) << endl; // 第一个 3.14,第二个 0 -
-
除法不能用流水线
汇编
-
x86-64(又称 x64、AMD64)
是指令集架构(ISA)
是 x86 架构的 64 位扩展
是 指令集的 64 位版本-
地址转换 仍依赖 分页 机制
(4KB/2MB/1GB 页)
但新增 大页 支持
减少页表层级
提升地址转换效率 -
扩展 虚拟地址空间
-
扩展 寄存器 数量 和 位宽
-
指令集增强
- 兼容 32 位 x86 的 指令
- 64 位新增指令
- 专用指令扩展
-
-
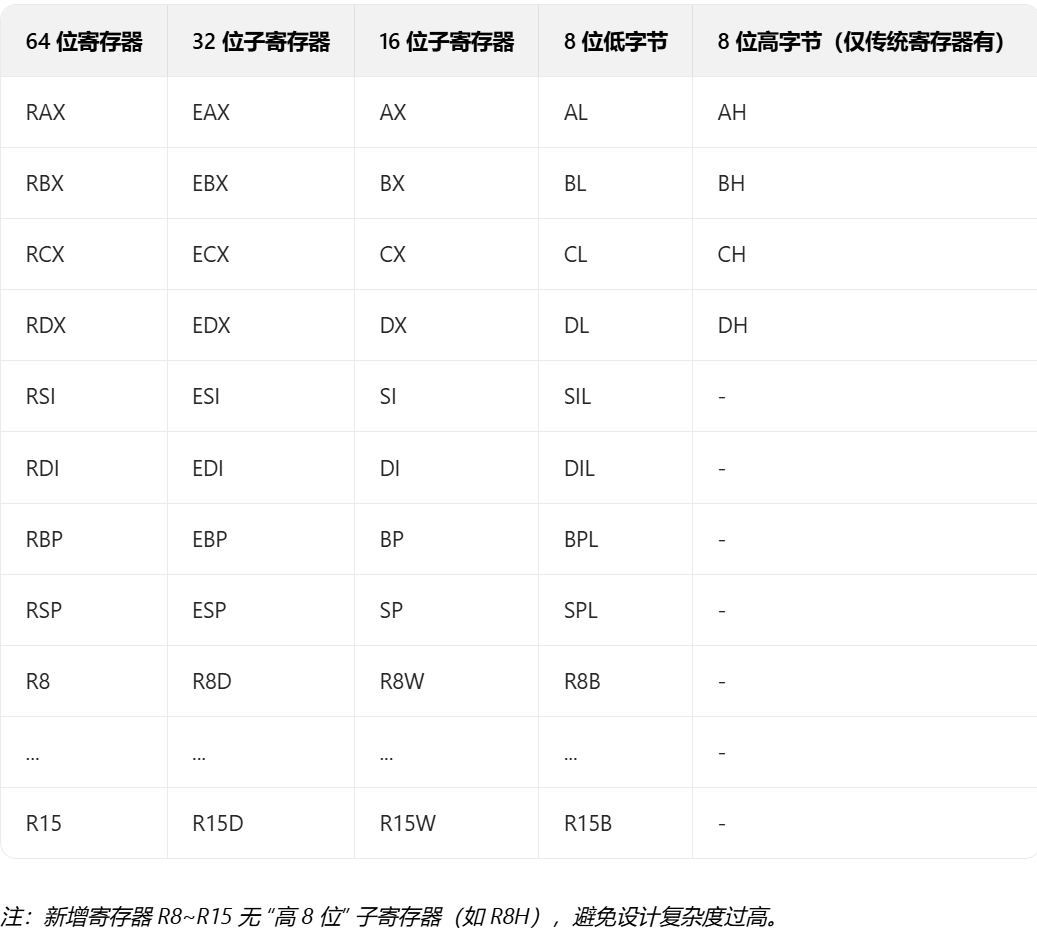
寄存器
-
64 位 通用寄存器
![image]()
-
可用通用寄存器总数从 8 个增加到 16 个
减少了 函数调用时 对栈内存的访问次数
显著提升了性能 -
栈指针 RSP
默认按 8 字节对齐
-
-
向量寄存器 / SIMD寄存器
-
SSE 系列
16 个 128 位 XMM 寄存器(XMM0~XMM15)
浮点运算、整数向量操作 -
AVX 系列
256 位 YMM 寄存器(YMM0 - YMM15)
512 位 ZMM 寄存器(ZMM0 - ZMM31) -
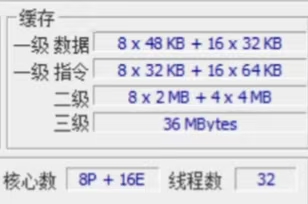
cpu-z
支持 XMM 寄存器 ← 包含 SSE/SSE2/SSE3/SSSE3/SSE4.1/SSE4.2
支持 YMM 寄存器 ← 包含 AVX/AVX2
支持 ZMM 寄存器 ← 包含 AVX-512
![image]()
-
-
指令指针 RIP
64 位版本的 IP(指令指针)
存储下一条要执行的 指令地址
支持 64 位 虚拟地址寻址 -
标志寄存器 RFLAGS
在 32 位 EFLAGS 基础上扩展
新增 地址大小位(AD),操作数大小位(OP)
用于切换 32/64 位 地址 / 操作数 模式-
ZF 零标志:计算结果为 0 时,ZF 为 1,否则为 0
-
OF 溢出标志:有符号数,运算时结果溢出,OF 为 1
-
CF 进/借位标志:无符号数,加法进位 or 减法借位时,CF = 1
-
SF 符号标志:符号位为 1,SF = 1
-
DF 方向标志:控制字符串操作的方向
-
IF 中断使能标志
-
-
控制寄存器(CR0-CR4、CR8)
-
控制 CPU 工作模式
(如保护模式、分页) -
缓存策略
-
-
调试寄存器(DR0-DR7)
-
硬件调试
-
设置断点
-
监视内存访问
-
-
段寄存器
-
cs:指向代码段(存储程序指令的内存区域)
-
ds:指向数据段(存储全局 / 静态数据的内存区域)
-
ss:指向栈段(存储栈数据段,函数调用上下文的区域)
-
es:扩展数据段
-
fs:
-
gs:
-
-
-
64 位版本的 Intel 指令集
英特尔处理器的汇编语言-
Intel 语法(Windows 常用)
指令 目的操作数, 源操作数 -
AT&T 语法(Linux / GCC 常用)
指令 源操作数, 目的操作数-
寄存器名前加 %
-
立即数前加 $
-
指令后缀:b/w/l/q 表示操作数宽度
b(byte,1 字节)
w(word,2 字节)
l(long,4 字节)
q(quadword,8 字节)
-
-
数据传输的方向
寄存器 ↔ 寄存器
寄存器 ↔ 内存
立即数 → 寄存器 / 内存- 不能直接从内存到内存
(必须经过寄存器中转)
- 不能直接从内存到内存
-
算术与逻辑操作
addq %rbx, %raxrax += rbx
subq %rbx, %raxrax -= rbx
imulq %rbx, %raxrax *= rbx(有符号)
imulq %rbx%rax 是默认被乘数
divq %rbxrax = rax / rbx(无符号,商在 rax,余数在 rdx)
cmpq %rbx, %rax计算 rax - rbx,不保存结果,只影响标志位
andq %rbx, %raxrax &= rbx
orq %rbx, %raxrax |= rbx
xorq %rbx, %raxrax ^= rbx
notq %raxrax = ~rax(按位取反)
negq %raxrax = -rax(取负)
incq %rcx自增
incq (%rsp)栈顶内存值加 1
decq %rdx自减
decq 8(%rbp)该内存值减 1
shlq / salq:左移
shrq:逻辑右移
sarq:算术右移 -
控制转移
-
无条件跳转
jmp label:直接跳转到目标地址
callq func:函数调用
retq:函数返回 -
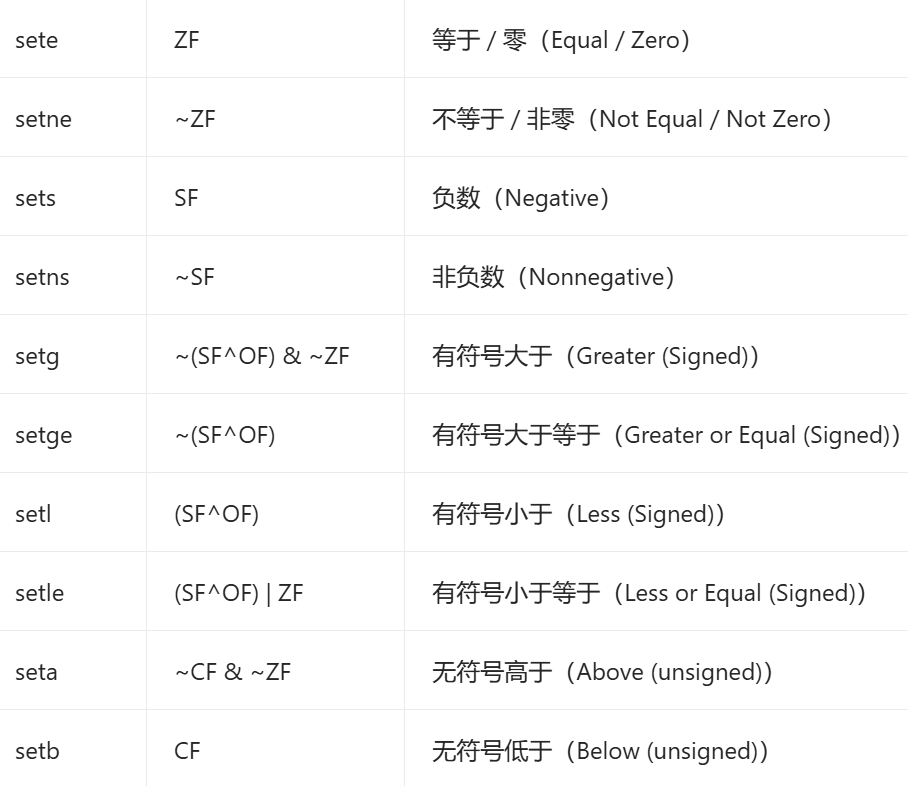
条件分支
je label# 相等(ZF=1)
jne label# 不相等(ZF=0)
jl label# 小于(有符号)
jg label# 大于(有符号)
jle label# 小于等于(有符号)
jge label# 大于等于(有符号)
![image]()
-
-
内存寻址
-
直接寻址
movl 0x1234, %eax -
寄存器间接寻址
movl (%ebx), %eax
从 EBX 指向的内存地址读取值到 EAX-
%ebx = 0x1000
内存地址 0x1000 处的值是 0x12345678 -
结果:%eax = 0x12345678
-
以 %ebx 的值 0x1000 作为内存地址
取出该地址的 4 字节(long)内容
放入 %eax -
相当于 temp = *ptr
-
-
基址 + 位移寻址
-
movq -8(%rsp), %rax
从地址 [RSP - 8] 读取值 -
movl 4(%ebp), %eax
从地址 [EBP + 4] 读取值
-
-
基址 + 索引寻址
-
movl (%ebx,%esi), %eax
从地址 [EBX + ESI] 读取值 -
movq (%rdi,%rcx), %rax
从地址 [RDI + RCX] 读取值
-
-
基址 + 索引 × 比例 + 位移
-
movl 8(%ebx,%esi,4), %eax
从地址 [EBX + ESI×4 + 8] 读取值 -
movq 16(%rdi,%rcx,8), %rax
从地址 [RDI + RCX×8 + 16] 读取值 -
比例因子只能是 1,2,4,8,不能是寄存器
-
-
-
加载有效地址(load effective address)
leaq 源操作数(地址模式), 目的寄存器-
movq (%rax), %rbx
会读取%rax指向的内存数据
存入%rbx(访问内存) -
leaq (%rax), %rbx
仅计算%rax的值(即地址本身)
存入%rbx(不访问内存,只做地址计算) -
取地址
int *p = &arr[3];
对应
leaq 12(%rdi), %rax -
计算算术表达式
leaq (%rdi,%rdi,2), %rax
计算3x-
由于地址模式中的D(Rb, Ri, S)
可以表示Rb + Ri×S + D
而S只能是 1、2、4、8、…… -
这恰好匹配很多算术表达式的形式
(如x + k*y,k=1/2/4/8)
因此leaq常被编译器用来快速计算这类表达式
-
-
-
System V AMD64 ABI
x86-64 Linux 环境下的函数参数传递约定- 第一个参数:%rdi
- 第二个参数:%rsi
- 第三个参数:%rdx
- 第四个参数:%rcx
- 第五个参数:%r8
- 第六个参数:%r9
-
-
微架构:架构的具体实现
示例:缓存大小和核心频率 -
机器码:处理器执行的字节级程序
汇编代码:机器码的文本表示形式
lab3
-
多字节数据(如函数地址、cookie 值)在内存中的字节排列顺序
-
栈帧的布局,包括
- 局部变量
- 返回地址
- 函数参数在栈中的存储位置
-
call指令压入返回地址
ret指令弹出返回地址并跳转的原理 -
缓冲区溢出的成因
- Gets/gets等函数无边界检查
- 输入过长字符串会覆盖栈上的返回地址
-
rtarget 采用了两种防护机制抵御 cl
- 栈地址随机化(破坏代码注入的地址确定性)
- 栈内存不可执行(阻止注入代码运行)
-
绕过防护
-
面向返回编程(ROP)
-
代码注入攻击(CI)
- 通过缓冲区溢出覆盖函数返回地址
使其跳转到注入的自定义代码
再由注入代码调用目标函数并传递指定参数
- 通过缓冲区溢出覆盖函数返回地址
-
-
objdump -d
获取目标程序的汇编代码
分析函数地址、指令序列、gadget 位置 -
GDB
观察栈的实时状态
验证缓冲区溢出的覆盖范围
返回地址的修改效果
攻击字符串的执行流程 -
攻击字符串生成工具(HEX2RAW)
将十六进制格式的指令 / 地址 / 数据
转换为原始字节字符串
同时规避 0x0a(换行符)等非法字节 -
你的解决方案不得通过攻击绕过程序中的验证代码。
具体而言,
攻击字符串中包含的、供ret指令使用的任何地址,
必须指向以下目标之一:-
touch1、touch2或touch3函数的地址
-
你注入的代码的地址
-
来自gadgets库的某个 gadget(代码片段)的地址。
-
你只能从rtarget文件中、start_farm和end_farm函数之间的地址范围提取 gadgets
-
-
ctarget和rtarget支持多个命令行参数:
-h:打印所有可用命令行参数的列表。
-q:不将结果发送至评分服务器。
-i FILE:从指定文件读取输入,而非从标准输入读取
系统级io
-
unix 库,如 printf 和 scanf,以及 例程
- 错误处理例程
- perror:只打印一条错误消息
- 错误处理例程
-
低级 io 直接面向操作系统的接口
-
级别略高于操作系统的 系统软件
-
unix 和其他操作系统都支持低级 io
-
rio:健壮的 io 包
-
应用程序:例如受 不足值 影响的网络程序
-
二进制数据的 无缓冲 输入输出
rio_readn 和 rio_writen-
与 Unix 的read和write接口一致
尤其适用于在网络 套接字 上传输数据 -
rio_readn仅在遇到 EOF 时才会返回不足值
仅在你明确要读取的字节数时使用它 -
rio_writen绝不会返回不足值
-
可在同一个文件描述符上
交错调用 rio_readn 和 rio_writen -
当 read() 被 信号中断 时
重新尝试读取
if (errno == EINTR) // 被信号处理函数中断 nread = 0; -
-
文本行与二进制数据的 带缓冲 输入
rio_readlineb 和 rio_readnb-
特别适用于从网络 套接字 读取文本行
-
停止条件
-
读取了 maxlen 个字节
-
遇到 EOF
-
遇到换行符 ('\n')
-
-
带缓冲的 RIO 函数是 线程安全 的
-
可在在同一描述符上
交错调用 rio_readlineb 和 rio_readnb -
不要与 rio_readn 的调用交错使用
-
-
-
-
缓冲
-
标准 io 库
带缓冲(c 语言的 printf 和 scanf)
全缓冲、行缓冲、无缓冲
减少 系统调用 次数,提升 I/O 效率-
stdout:行缓冲
遇到 换行符\n 或 缓冲区满 时,自动刷新缓冲区 -
stderr:无缓冲
没有缓冲区,数据直接写入内核
调用写函数就立刻触发内核调用 -
全缓冲:
所有通过 fopen() 打开的「磁盘文件」
只有缓冲区被写满时,才会刷新缓冲区
-
-
Unix I/O(系统调用级 I/O)
无缓冲:每次读写都直接进入内核 -
缓冲 I/O,读取
-
rio_buf:缓冲区的起始地址
-
rio_bufptr:缓冲区的 当前读取指针
指向 “已从文件读入缓冲区,但还没被应用程序读取” 的字节段的起始点 -
rio_cnt:缓冲区中 未被应用程序读取 的字节数
-
先给目标文件分配一个关联的 内存缓冲区
-
系统调用 从文件中读取数据,填满整个缓冲区
-
rio_cnt 等于缓冲区大小
-
rio_bufptr 指向缓冲区开头
-
-
应用程序 请求读取
-
如果 rio_cnt > 0
-
直接从 rio_bufptr 指向的位置读取数据
-
rio_bufptr 向后移动
-
rio_cnt 减少对应的字节数
-
-
如果 rio_cnt == 0
-
系统调用,从文件中读取新的数据,重新填满缓冲区
-
rio_bufptr 和 rio_cnt 被重置
-
-
-
-
-
与 Windows 不同,Unix 不区分文件类型
-
在 Linux 中,所有文件的底层本质都是连续的字节流
-
一个Linux文件是m个字节的序列:B₀、B₁、…、Bₖ、…、Bₘ₋₁
-
字节的具体含义(如文本的字符、图片的像素、程序的机器码)由应用程序而非内核解析
-
Unix/Linux 将所有硬件 I/O 设备都抽象为 设备文件(存放在/dev目录下)
- /dev/sda2:表示磁盘分区(块设备)
- /dev/tty2:表示终端设备(字符设备)
-
设备无关性
应用程序可以用统一的文件操作接口(open/read/write/close)操作硬件
无需针对不同设备编写专用驱动逻辑 -
Linux 内核本身也被抽象为文件形式,分为 内核镜像文件 和 内核数据的虚拟文件系统 两类
-
/boot/vmlinuz-3.13.0-55-generic:内核镜像文件
-
/proc:伪文件系统。
并非实际存储在磁盘的文件
而是内核在内存中动态生成的 “虚拟文件” 集合
-
-
内核为所有 I/O 操作提供了统一的系统调用接口
-
open:内核会为 进程 分配一个 文件描述符
-
返回为负:无法打开文件
-
不是有效的文件描述符
-
是系统调用(如 open)的错误返回值
-
可能原因有文件不存在,权限不足
-
-
0 标准输入
-
1 标准输出
-
2 标准错误
- 输出程序的错误信息
-
-
close:释放 进程 占用的 文件描述符 和 内核中对应的文件资源
-
在 多线程 程序中,关闭一个已关闭的文件会引发严重问题
-
多线程程序中
可能有两个程序同时运行
共享数据结构,彼此交互,共享内存
-
-
read:从 文件的当前位置 读取数据到 应用程序的缓冲区,返回实际读取的字节数
-
调用时
要给出文件描述符
给出一个指向 缓冲区 的指针
指定缓冲区的长度
(避免溢出) -
缓冲区可通过 静态 或 malloc 分配
-
在标准输入中
read 将 挂起并等待
直到你输入一个字符串,然后回车
它就会将该字符串的至少一部分内容读入程序中 -
在网络连接中
read 将 挂起并等待
直到新内容进入
它才会读入若干字节- 若干:它读入的字节数不是固定的
最多不超过缓冲区的长度
- 若干:它读入的字节数不是固定的
-
不足值 k
read的 实际读取字节数k < 指定的最大字节数-
读取时遇到文件结束符(EOF)
-
从终端读取文本行
-
读写网络 数据包
-
很长的消息会被分割成多个小数据块
每块通常 1000 个字节 -
实际取决于它要通过的是协议中的哪一层
但一般是 1500 个字节,这就是标准的 最小传输单元
一个大的文件就会被分割成像那样的小数据块 -
如果想将该文件读入一个较大的缓冲区
它通常也是按块读入
-
-
-
返回值如果是 0
表示检测到 EOF
说明执行到 文件结尾
或 网络连接已关闭
-
-
write:将 应用程序缓冲区 的数据写入 文件的当前位置,返回实际写入的字节数
- 不足值
通过网络发送数据包时
它只会发送该包可以容纳的字节数
然后返回,你必须把数据抽取出来按包发送
通常在编写使用 while 循环的代码时
必须考虑到不足值的情况
- 不足值
-
lseek:显式调整文件的 当前偏移量
-
终端的输入
无法移动,恢复,备份先前已经读入的数据
无法提前接收未键入的数据 -
网络套接字
无法在时间上跳转
只能在 数据包进入 时对其进行读或写
-
-
提供了访问文件 元数据 的函数
-
异步信号安全
-
复杂,易出错
-
处理不足值
-
高效读取文本行
-
-
-
系统级调用 的开销是比较大的
这将操作过程全抛给 操作系统,执行 上下文切换
它会进入系统内核,调用操作系统函数
按指令完成读、写操作,再切回到先前的工作 -
每次进行 系统调用 时都应该检查 返回值
-
普通文件,放在 磁盘驱动器
-
目录
-
条目 描述其他文件的位置和属性
-
目录由一个 链接数组 构成
-
每个链接将一个文件名映射到一个文件
-
每个目录至少包含两个条目
.(点)是指向自身的 链接,表示当前目录自身
..(点点)是指向目录层级结构中 父目录 的链接,表示树形结构中当前目录的父目录 -
内核会为每个 进程 维护一个 当前工作目录(cwd)
-
进程默认会在这个目录下执行文件操作(如创建、读写文件),无需指定完整路径
-
可以通过 cd 命令修改当前工作目录
-
-
目录是指向其子目录的指针
-
绝对路径名:以 “/” 开头,表示从 根目录 开始的路径
- 例如
/home/droh/hello.c
- 例如
-
相对路径名:表示从当前工作目录开始的路径
- 例如
../home/droh/hello.c
- 例如
-
![image]()
-
-
网络连接 / 套接字
-
消息 是写入套接字来 发送 的,从套接字读出来 接收 的
-
套接字:接收、发送消息
-
-
在 应用程序 之间传送数据的 通道文件
- 既是前一程序的输出
- 也是后一程序的输入
-
符号链接文件
- 不需要创建副本就可以有多个名称、被多个指针指向
-
应用程序 通常会区分文本文件与二进制文件
-
文本文件:仅包含 ASCII 或 Unicode 字符的普通文件
-
Unicode:可对 非英文字符 进行编码
-
文本行是由换行符(\n)结尾的字符序列
-
Linux 与 Mac OS:使用 \n
对应换行符(LF) -
Windows 与互联网协议:使用 \r\n
对应 “回车符(CR)后接换行符(LF)”
-
-
二进制文件:其余所有类型的普通文件
- 目标文件、JPEG 图片
-
内核 并不会区分这两者
-
-
文件元数据:描述文件数据的信息
-
每个文件的元数据由 内核 维护
-
用户可通过 stat 和 fstat 函数访问元数据
-
stat
struct stat { dev_t st_dev; // 文件所在设备ID ino_t st_ino; // inode编号 mode_t st_mode; // 保护模式和文件类型 nlink_t st_nlink; // 硬链接个数 uid_t st_uid; // 所有者用户ID gid_t st_gid; // 所有者组ID dev_t st_rdev; // 设备ID(如果是特殊文件) off_t st_size; // 总体尺寸,以字节为单位 unsigned long st_blksize; // 文件系统 I/O 块大小 unsigned long st_blocks; // 已分配块个数 time_t st_atime; // 上次访问时间 time_t st_mtime; // 上次更新时间 time_t st_ctime; // 上次状态更改时间 };- st_mode 的低 9 位是 权限位
所有者 权限:前 3 位
所属组 权限:中间 3 位
其他用户 权限:最后 3 位
如 rwx 对应可读、可写、可执行
- st_mode 的低 9 位是 权限位
-
编译时常量 / 宏 可查看并检查 元数据
-
chmod 修改文件权限
- 把文件的所有权限位全部置 0
八进制权限0000
即关闭所有读 / 写 / 执行权限
- 把文件的所有权限位全部置 0
-
-
Unix 内核 如何表示 已打开的文件
-
描述符表:进程私有
-
每个进程一个表
-
存储 文件描述符(fd)
-
stdin = fd0、stdout = fd1、stderr = fd2
-
用户打开的文件从 fd3 开始
-
每个 fd 是一个指针
指向打开文件表中的某个条目
(代表一个打开的文件实例) -
进程连续调用两次open("同一个文件名", ...)
会得到两个 不同 的文件描述符 -
父进程执行 fork() 创建子进程时
子进程 继承 父进程的打开文件
子进程会 复制 父进程的描述符表 -
进程间的 fd 隔离
(每个进程的 fd 含义独立)
-
-
打开文件表:所有进程共享
-
每个条目对应一个 文件打开实例
- 同一个物理文件
多次打开会生成多个实例
- 同一个物理文件
-
动态状态字段
-
File pos:文件当前的读写位置(偏移量)
-
refcnt:引用计数
记录有多少个 描述符表的 fd 指向当前条目
-
-
当 进程 调用 open 打开文件时
内核会创建 打开文件表条目
并将其 refcnt 设为 1 -
内核会让新 fd 指向同一个 打开文件表条目
并将 refcnt 加 1-
若父进程执行 fork() 创建子进程
-
若进程调用 dup(复制 fd)
-
-
当进程调用 close(fd) 时
内核会将对应 打开文件表条目 的 refcnt 减 1- 只有当 refcnt=0 时
内核才会释放该条目
(真正关闭文件实例)
- 只有当 refcnt=0 时
-
若两个 fd 指向 不同 的打开文件表条目
(即使是同一个物理文件)
它们的 File pos 是 独立 的
(各自读写自己的位置); -
若两个 fd 指向 同一个 打开文件表条目
它们 共享 File pos-
如 dup 复制的 fd
-
比如子进程的fd和父进程的fd
会指向同一个「打开文件表」条目- 如果此时要关闭文件
所有进程都必须调用 close
- 如果此时要关闭文件
- 一个 fd 读写后
另一个 fd 的读写位置会随之变化
-
-
-
v-node 表:所有进程共享
-
每个条目对应一个物理文件的静态元数据
(与 stat 结构体的内容一致) -
同一物理文件的所有 打开实例
都共享同一个 v-node 条目
-
-
-
I/O 重定向
-
改变程序默认的输入 / 输出目标
-
标准输出重定向
用 < 符号表示将写出到标准输出重定向到写出到文件 -
打开目标文件
得到一个新的文件描述符 -
执行 dup2(4, 1)
修改描述符表-
fd4 对应的描述符表项(记为 b)
指向 foo.txt 的 打开文件表条目 -
执行前
fd1 对应的描述符表项(记为 a)
仍指向默认的标准输出(终端) -
执行后
fd1 的表项被替换为 b
fd1 现在也指向 foo.txt 的 打开文件表条目- 当描述符不再指向该条目时,refcnt减 1
-
-
调用 execvp("ls", ...) 启动 ls 进程
-
ls 继承 Shell 的描述符表
- 其 fd1 指向 foo.txt,而非终端
-
输出重定向生效
ls 的输出写入 fd1,即写入 foo.txt
-
-
标准 I/O 函数
-
打开与关闭文件(fopen 和 fclose)
-
读写字节(fread 和 fwrite)
-
读写文本行(fgets 和 fputs)
-
格式化读写(fscanf 和 fprintf)
-
标准 I/O 将 “已打开的文件” 抽象为 流
流是对 文件描述符 + 内存缓冲区 的高层封装抽象 -
FILE*
标准 I/O 中表示 流 的结构体类型
stdin/stdout/stderr 都是 FILE* 类型的指针
指向对应的流对象 -
缓冲区会在以下场景被刷新到输出文件描述符:
-
遇到换行符\n时(仅对行缓冲有效)
-
调用fflush函数时
-
程序调用exit退出时
-
从main函数返回时
-
刷新
-
用户态缓冲区 → 内核态 的数据搬运
唯一的一次内核调用 -
C 标准库自动调用 底层write(fd, buf, n) 系统调用
将用户态缓冲区中积攒的所有数据
一次性写入 到对应的文件描述符(stdout)
写完后 清空 缓冲区
-
-
-
非常适用于对 终端/文件 执行 I/O 操作
不太适用于 网络连接 -
不足值 的情况会被自动处理
-
没有提供访问文件元数据的函数
-
标准 I/O 函数不是异步信号安全的
不适合在信号处理器中使用
-
-
不能用于二进制文件
-
面向 文本 的 I/O 函数
-
如fgets、scanf、rio_readlineb
-
它们会解析行结束(EOL)字符
-
改用rio_readn或rio_readnb这类函数
-
-
字符串 函数
-
如strlen、strcpy、strcat
-
会将字节值 0(字符串结束符)视为特殊字符
-
-
-
根目录 / 下包含以下 子目录 及内容:
-
bin/:存放可执行程序
- 包含 bash(bash 命令解释器);
-
dev/:存放设备文件
- 包含 tty1(终端设备文件);
-
etc/:存放系统配置文件
- 包含 group(用户组配置文件)
- passwd(用户账户配置文件)
-
home/:存放用户主目录
- 包含 droh/、bryant/ 两个用户目录
- droh/ 下有 hello.c 源文件
-
usr/:存放系统共享资源
-
包含 include/(头文件目录)
- 含 stdio.h
- sys/(系统头文件目录,含 unistd.h)
-
bin/(存放应用程序,包含 vim(文本编辑器))
-
-
期末突击
-
cpp 是 C 预处理器,不是 C++ 编译器
处理源代码中的 #include(头文件包含)、#define(宏替换)、条件编译等指令,生成一个“纯净”的 .i 文本文件 -
ccl 是 GCC 内部的编译器组件
-
as 是 GNU 汇编器
-
ld 是 GNU 链接器
-
重定位:
确定程序各部分在内存中的最终地址
你(链接器/加载器)把各个房间的家具(代码段、数据段)搬进新房子(内存地址空间),然后必须把房子里所有写着旧地址的文件(指令中的地址引用)都手动修改为新地址(重定位),否则信件(CPU访问)就找不到地方。 -
重定向:
你告诉快递员把包裹送到“A地址”(发起请求)。A地址的前台(重定向执行者)看了一眼说:“收件人已搬去B地址了”(返回重定向响应)。快递员于是把包裹改送到B地址。 -
全局变量(外部链接)
其符号名会被放入目标文件的符号表 (.symtab)
并标记为 GLOBAL
链接器在链接多个目标文件时
需要处理所有对它的引用 -
静态变量(内部链接或无链接)
-
静态 全局 变量
其符号名会被标记为 LOCAL -
静态 局部 变量
不放入符号表 -
链接器不需要处理跨文件的引用
简化链接过程
避免符号冲突
-
-
定义符号的库要放在引用它的文件之后
-
多个库之间存在依赖
(比如 x 调用 y,y 调用 z)
库的顺序要遵循
「调用者在前,被调用者在后」的拓扑序
听课记录
-
用补码
- 不存在+0,-0
-
字长
-
数据的存储
每个字节有一个地址
连续
记其中一个地址
用最低的地址作为整个数据的地址
符号对齐
告诉我类型是什么 -
数值编码:正数的符号位0,负数的符号位1,剩余位作为数值部分,机器数的不变,真值
机器数:存在机器内的连同正负符号一起数码化的数
这个机器数的真值:它真正表示的数值
机器数比真值多一个符号位 -
存储器按字节编址
-
大端:msb所在的地址是
lsb -
面向内存编程
-
专用寄存器
-
标志寄存器 or 程序/状态字寄存器
-
x86:变长指令字
-
操作系统分配空间
-
将表达式编译为指令序列,计算机直接执行指令来完成运算
-
MIPS
-
sel
-
累加器al / ax / eax
-
linux 环境 和 gcc 工具链
操作系统





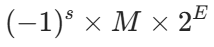
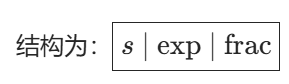




 浙公网安备 33010602011771号
浙公网安备 33010602011771号