数的存取

进制转换

转为十进制

二进制，八进制，十六进制转化为十进制都只要遵循“按权相加”即可。
假设但是数字是N进制，那么：

• 整数部分：从右往左看，第i位的位权等于\(N^{i-1}\)
• 小数部分：从左往右看，第j位的位权等于\(N^{j}\)

Exp1：将八进制的53627转换为十进制
答：\(53627 =\,\,5\times 8^4+3\times 8^3+6\times 8^2+2\times 8^1+7\times 8^0=22423\)

---

Exp2：将八进制423.5176转换为十进制
答：整数部分略过；小数部分：\(.5176=\,\,5\times 8^{-1}+1\times 8^{-2}+7\times 8^{-3}+6\times 8^{-4}=0.655761719\)

十进制转换为其他进制

十进制转化为其他进制比较复杂，整数和小数部分需要分开讨论：

1. 整数部分
   十进制转换为N进制整数时，采用“除N取余，逆序排列”

steps:

• 将N作为除数，用十进制的整数除以N，可以得到商和余数；
• 保留余数，重复step1；
• 重复step2，直到商为0为止；
• 先得到的余数作为低位，后得到的余数作为高位，依次排列

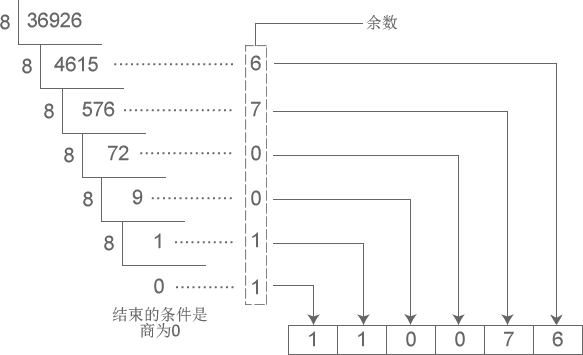
这个运算相当于将其他进制整数转换为十进制整数的逆运算

2. 小数部分
   十进制小数转化为N进制小数，遵循“乘N取整，顺序排列”

steps:

• 用N乘以十进制小数，得到一个积，这个积包含了整数和小数；
• 将积的整数保留，用N再乘以余下的小数部分，又可以得到一个新的积；
• 重复step1和2；
• 直到积的小数部分为0结束
• 将保留的积按照得到的顺序从左往右依次排列

参考链接

计算机中数的表示_是小白哇的博客-CSDN博客