机器学习||李宏毅课程笔记④自注意力机制(Self-attention)
这是李宏毅老师机器学习【第四节课程】的笔记(仅用于个人学习记录),本节课程简单对自注意力机制(Self-attention)进行了介绍。
一、引入
在实际应用中,数据可能会有各种各样的形式,我们可能需要对输入的任意长度个向量进行处理。
从输入看:
- 文字处理(自然语言处理)
- 将word表示为向量
- one-hot
- word-embedding
- 将word表示为向量
- 声音信号处理
- 每个时间窗口(Window, 25ms)视为帧(Frame),视为向量
- 图
- 每个节点视为一个向量
- Social graph(社交网络图)
- 分子式【one-hot】
- 每个节点视为一个向量
从输出看:
- 输入输出数量相等【每个向量都有一个标签】⇒sequence Labeling
- 词性标注(POS tagging)
- 语音辨识(每个vector对应phoneme)
- 社交网络(每个节点(人)进行标注【是否推送商品】)
- 整个输入序列只有一个输出
- 文本情感分析
- 语者辨认
- 分子的疏水性
- 由模型决定输出的数目【seq2seq】
- 翻译
- 语音辨识
二、Self-attention简介
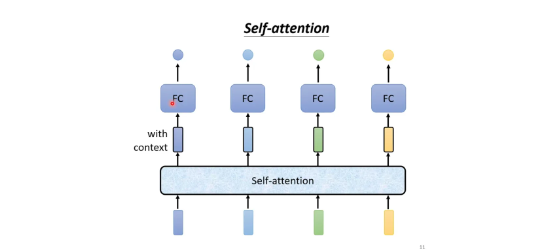
特点:考虑整个序列sequence的所有向量,综合向量序列整体和单个向量个体,得到对每一个向量处理后的向量
⇒将这个向量链接一个FC,FC可以专注于处理这一个位置的向量,得到对应结果。
Self-attention+FC可以交替使用
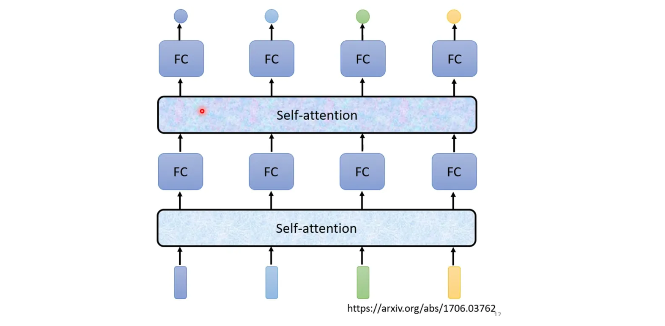
三、Self-attention细节
基本原理
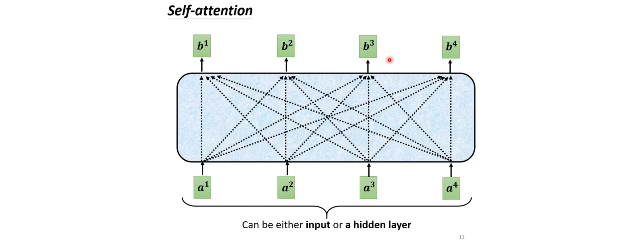
输入:一串的Vector,那这个Vector可能是你整个Network的Input,它也可能是某个Hidden Layer的Output
输出:处理Input以后,每一个b都是考虑了所有的a以后才生成出来的
具体步骤
-
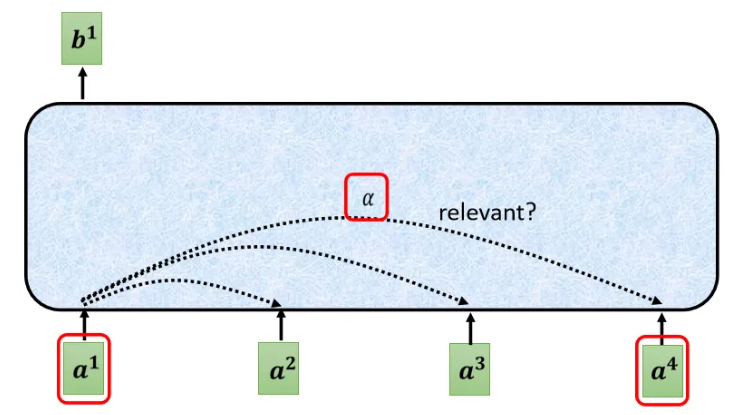
根据 \(a^1\)这个向量,找出整个sequence裡面,跟 \(a^1\)相关的其他向量⇒哪些部分是重要的【判断label,决定class,决定regression数值】用 \(\alpha\)表示
![image]()
-
计算Attention的模组:拿两个向量作为输入,输出 \(\alpha\)
\(q\)=query
\(k\)=key
![image]()
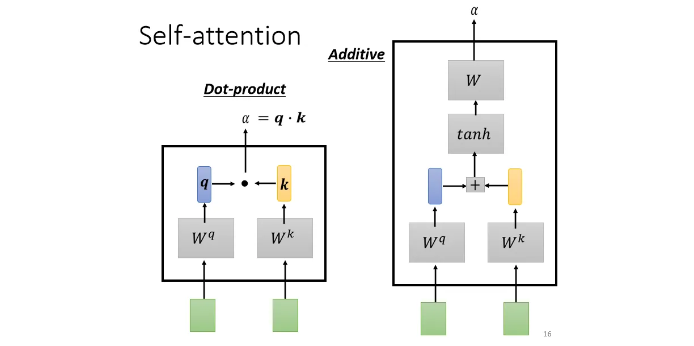
方法一 dot product:
输入的这两个向量分别乘上两个不同的矩阵,左边这个向量乘上矩阵 \(W^q\)得到矩阵 \(q\),右边这个向量乘上矩阵 \(W^k\)得到矩阵 \(k\);再把 \(q\)跟 \(k\)做dot product,逐元素相乘后累加得到一个 scalar就是α
方法二 Additive:
得到 \(q\)跟 \(k\)后,先串接起来,再过一个Activation Function(Normalization),再通过一个Transform,然后得到 \(\alpha\).
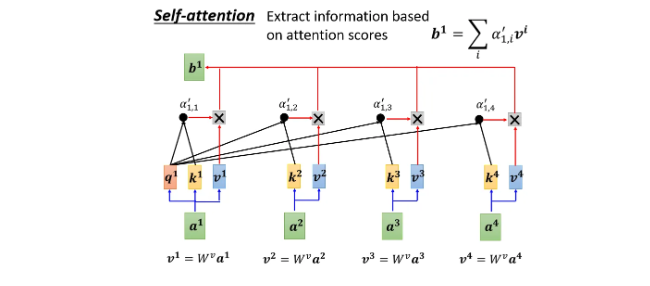
需要计算:任意两个向量之间的关联性,作softmax【不一定要用,也可以用其他激活函数】,得到\(\alpha '\)
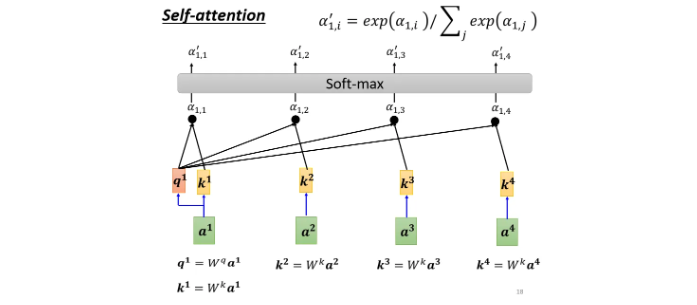
- 分别抽取重要信息,根据关联性作加权求和得到 \(b\):query key value
![image]()
矩阵的角度
Step \(I\) 计算 \(k,q,v\)
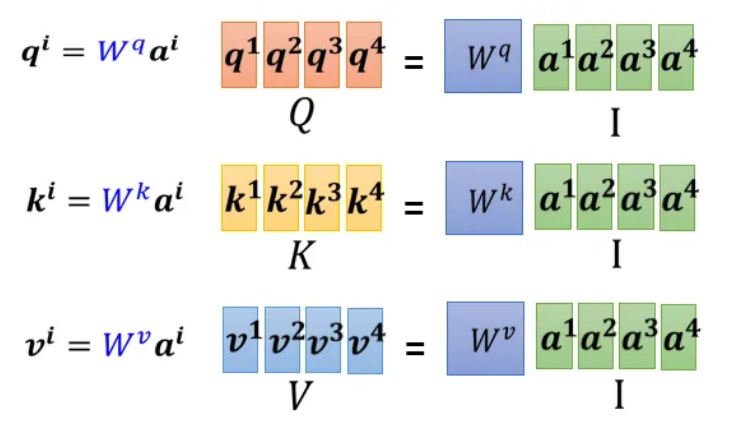
\(W^q,W^k,W^v\)是三个要学习的网络参数矩阵
Step \(II\) 计算 \(\alpha\)并Normalization

Step \(III\) 计算 \(b\)
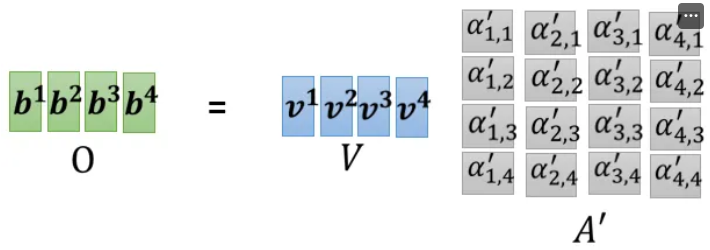
综合:
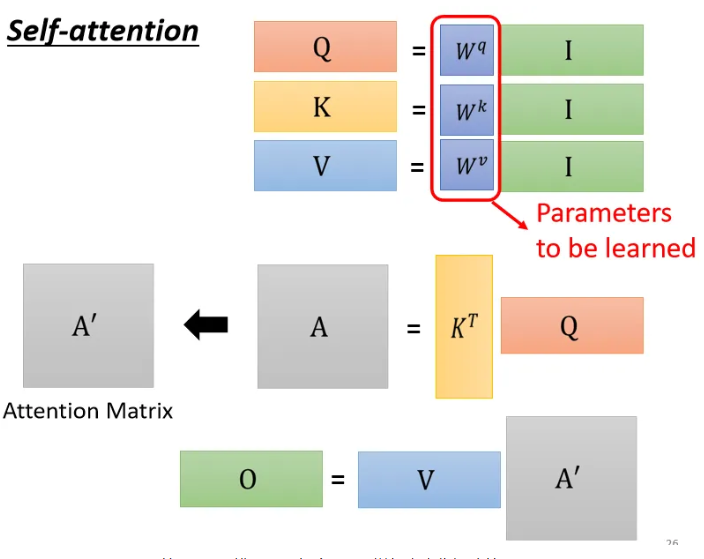
- I 是 Self-attention 的 input一排vector,每个vector拼起来当作矩阵的 column
- 这个 input 分别乘上三个矩阵, 得到 Q K V
- 这三个矩阵,接下来 Q 乘上 K 的 transpose,得到 A 。可能会做一些处理,得到 \(A'\) ,叫做Attention Matrix ,生成Q矩阵就是为了得到Attention的score
- \(A'\)再乘上 V,就得到 O,O 就是 Self-attention 这个 layer 的输出,
唯一需要学的参数:三个矩阵
四、Multi-head Self-attention(多头自注意力机制)
相关这件事情有很多种不同的形式:使用多个 q,k,v组合,不同的 q,k,v 负责不同种类的相关性
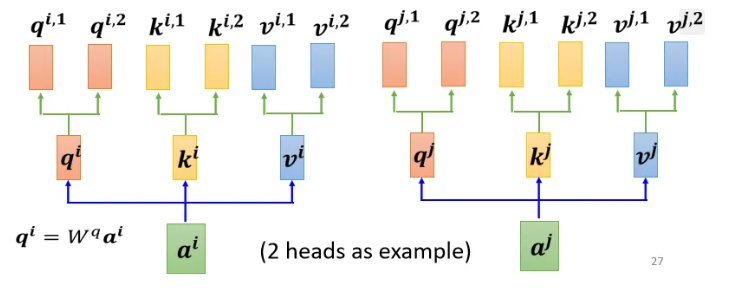
- 先把 a 乘上一个矩阵得到 q
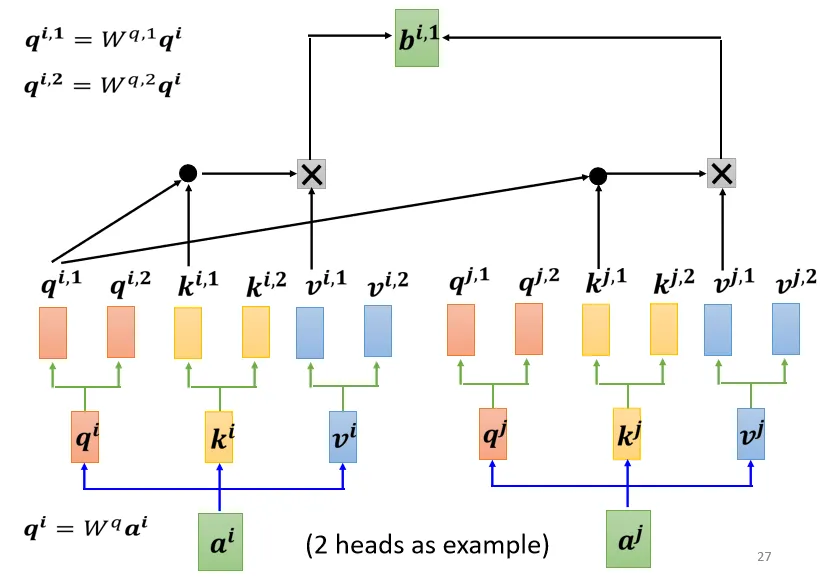
- 再把 q 乘上另外两个矩阵,分别得到 \(q^1\) 跟\(q^2\) ,代表有两个 head;同理可以得到 \(k^1\), \(k^2\), \(v^1\), \(v^2\).
- 同一个“头”里的k,q,v计算b.
![image]()
将各个头计算得到的 \(b\)拼接,通过一个 transform得到 bi,然后再送到下一层去
![image]()
五、Positional Encoding
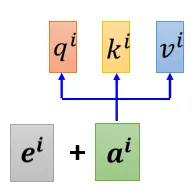
每个向量所处的“位置”需要被编码
每个位置用一个vector \(e^i\)来表示它是sequence的第i个。加和到原向量中。



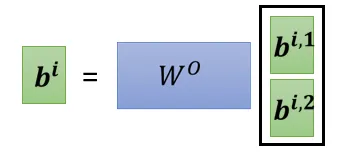

 浙公网安备 33010602011771号
浙公网安备 33010602011771号