唯一分解定理

1.唯一分解定理，也叫算术基本定理，指的是任何n>=2,都可以分解为n=p1*p2*p3*.....pn，其中pi为质数。

其包括两个断言：断言1：数n可以以某种方式分解成素数乘积。

                             断言2：仅有一种这样的因数分解。（除因数重排外）。

其可以化简为

 

 

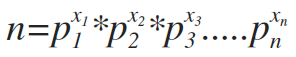
2.如何实现：

实现方法1

#include <bits/stdc++.h>
#define maxn 10005
typedef long long ll;
using namespace std;
int main()
{

    int n,i=0;
    int cnt=0;
    int a[maxn]={0};//存储其所有因子
    scanf("%d",&n);
    for(i=2;i*i<=n;i++)
    {
        while(n%i==0)
        {
            a[cnt++]=i;
            n/=i;
        }
    }
    if(n>1)
        a[cnt++]=n;
    for(i=0;i<cnt;i++)
    {
        if(i) printf(" ");
        printf("%d",a[i]);
    }
    printf("\n");
    return 0;
}

 

　　实现方法2：

我们要的其实是n的所有素数因子，所以我们只要预先用欧拉筛打个素数表，遍历的时候就只用遍历素数了，这样可以快一点，并且可以处理1e12以内的数。

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
int prime[10000005];
int a[1000005];
bool vis[10000005];
int cnt=0;
void primejudge(int n)
{
    memset(vis,false,sizeof(vis));
    vis[1]=true;
    int i,j;
    for(i=2;i<=n;i++)
    {
        if(!vis[i]) prime[cnt++]=i;
        for(j=0;j<cnt&&i*prime[j]<=n;j++)
        {
            vis[i*prime[j]]=true;
            if(i%prime[j]==0) break;
        }
    }
}
int main()
{

    primejudge(10000005);//预处理了1e7以内的素数
    ll n;
    int i,index=0;
    scanf("%lld",&n);
    for(i=0;i<cnt&&prime[i]*prime[i]<=n;i++)
    {
        while(n%prime[i]==0)
        {
            a[index++]=prime[i];
            n/=prime[i];
        }
        if(n==1) break;
    }
    if(n!=1)
    {
        a[index++]=n;//这一步的意思是。如果遍历到了1e7的素数，n还没有变为1，那么剩下的n一定是一个素数。（前提，n<1e12)
    }
    for(i=0;i<index;i++)
    {
        if(i) printf(" ");
        printf("%d",a[i]);
    }
    printf("\n");
    return 0;
}

　　应用1：

计算因子有多少个。设f(x)表示x的因子数，则f(a)=(1+x1)*(1+x2)*(1+x3)......(1+xn)，将上代码改造一下，就可以求得f(a).