51Nod 1686 第K大区间（离散化+尺取法）

http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1686

题意：

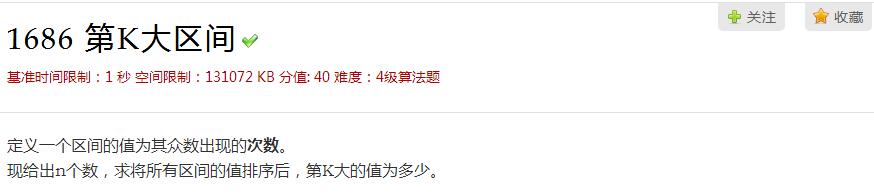
思路：

第K大值，所以可以考虑二分法，然后用尺取法去扫描，但是直接扫描肯定是不行的，数太大，数组开不了那么大。

没想到可以用离散化来预处理，就是先将数组排序、去重，然后对于序列中的每一个数，计算出它的lower_bound值，原来相同的数肯定还是相同的，因为n小于等于1e5,所以原来很大的值，经过这样处理之后就会变得很小了。

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn = 1e5 + 5;

int a[maxn], b[maxn];
int cnt[maxn];
int n;
int k;

bool check(int x)
{
    int count=0;
    memset(cnt,0,sizeof(cnt));
    int L=1,R=1;
    while(R<=n)
    {
        cnt[a[R]]++;
        if(cnt[a[R]]>x)
        {
            count+=n-R+1;
            cnt[a[L]]--;
            L++;
            while(cnt[a[R]]>x && L<R)
            {
                count+=n-R+1;
                cnt[a[L]]--;
                L++;
            }
        }
        R++;
        if(count>=k)  return true;
    }
    return false;
}

int main()
{
    //freopen("D:\\input.txt","r",stdin);
    while(~scanf("%d%d",&n,&k))
    {
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&a[i]);
            b[i]=a[i];
        }
        sort(b+1,b+n+1);
        int num=unique(b+1,b+n+1)-(b+1);
        for(int i=1;i<=n;i++)
            a[i]=lower_bound(b+1,b+num+1,a[i])-(b+1);

        //枚举第k大的值
        int L=1,R=n;
        while(L<=R)
        {
            int mid=(L+R)/2;
            if(check(mid))  L=mid+1;
            else R=mid-1;
        }
        cout<<L<<endl;
    }
}