李宏毅机器学习HW2（逻辑回归）

问题引入

很简单，就是二分类问题。

 

数据处理

首先读入数据

def read_file():
    """读入数据"""
    x_train = pd.read_csv('X_train.csv')
    x_train = x_train.iloc[:, 1:].to_numpy()
    y_train = pd.read_csv('Y_train.csv')
    y_train = y_train.iloc[:, 1:].to_numpy()
    x_test = pd.read_csv('X_test.csv')
    x_test = x_test.iloc[:, 1:].to_numpy()
    # print(x_train.shape)
    # print(y_train.shape)
    # print(x_test.shape)
    return x_train, y_train, x_test

　　

总的可用于训练的数据为（54256，510），测试数据为（27622，510）。

接下来标准化

def normalize(X, train=True, X_mean=None, X_std=None):
    """标准化"""
    if train:  # 如果train为True，那么表示处理training
        # data，否则就处理testing data,即不再另算X_mean和X_std
        X_mean = np.mean(X, axis=0).reshape(1, -1)  # 求各列均值
        X_std = np.std(X, axis=0).reshape(1, -1)    # 求各列标准差

    X = (X - X_mean) / (X_std + 1e-8)  # X_std加入一个很小的数防止分母除以0
    return X, X_mean, X_std

接下来将一部分数据分出来当作验证集

def split_data(x_train, y_train, ratio):
    """将数据按ratio比例分成训练集和验证集"""
    x_validation = x_train[math.floor(ratio * len(x_train)):, :]
    y_validation = y_train[math.floor(ratio * len(y_train)):, :]
    x_train = x_train[:math.floor(ratio * len(x_train)), :]
    y_train = y_train[:math.floor(ratio * len(y_train)), :]
    # print(x_train.shape)
    # print(y_train.shape)
    # print(x_validation.shape)
    # print(y_validation.shape)
    return x_train, y_train, x_validation, y_validation

按照9：1的比例拆分，最后训练集为（43404，510），验证集为（10852，510）。

 

逻辑回归

逻辑回归的公式为$f_{w,b} = \frac{1}{1+e^{-z}}$，其中$z=w_1x_1+w_2x_2+···+x_nx_n$。将样本的特征值代入该式计算后，会得到一个（0，1）之间的概率值，以0.5为界限可以将其二分类。

现在给出一组训练数据：

 

 

 那么$f_{w,b} $这个函数可以正确分类的概率为：

$L(w,b)=f_{w,b}(x^1)f_{w,b}(x^2)(1-f_{w,b}(x^3))···f_{w,b}(x^n)$

所以我们的目的是找到使得$L(w,b)$最大的$w$和$b$。

然后我们把问题进行转换，寻找$w,b$，使得$-lnL(w,b)$最小。

 $-lnL(w,b)=-(lnf_{w,b}(x^1)+lnf_{w,b}(x^2)+ln(1-f_{w,b}(x^3))···)$

                  $=\sum_{i=0}^{n}-\hat{y^i}lnf_{w,b}(x^i)-(1-\hat{y^i})ln(1-f_{w,b}(x^i))$

 接下来梯度下降求解，懒得打公式了，直接上照片：

这梯度和线性回归是相同的。

def sigmod(z):
    '''返回sigmod函数'''
    return np.clip(1 / (1.0 + np.exp(-z)), 1e-8, 1-1e-8)   # 避免溢出，如果sigmoid函数的最小值比1e-8小，只会输出1e-8；而比1 - (1e-8)大，则只输出1 - (1e-8)


def f(x, w, b):
    '''返回概率值'''
    return sigmod(np.dot(x, w) + b)


def cross_entropy_loss(y_pred, y):
    """计算误差"""
    loss = -np.dot(y.reshape(1, -1), np.log(y_pred)) - np.dot((1-y).reshape(1, -1), np.log(1-y_pred))
    return loss[0][0]      # 这儿我计算出来就是1×1大小的二维数组


def gradient(x, y, w, b):
    """计算损失函数的梯度"""
    y_pred = f(x, w, b)
    w_grad = np.dot(x.T, y_pred - y)
    b_grad = np.sum(y_pred - y)
    return w_grad, b_grad


def shuffle(x, y):
    """打乱数据"""
    random_list = np.arange(len(x))
    np.random.shuffle(random_list)
    return x[random_list], y[random_list]


def accuracy(y_pred, y):
    """计算正确率"""
    acc = 1-np.mean(np.abs(y_pred - y))
    return acc

 

模型训练

这里我们使用批次梯度下降。

def train(x_train, y_train, x_validation, y_validation):
    """批次梯度下降"""
    w = np.ones((x_train.shape[1], 1))
    b = 1
    iter_time = 30   # 迭代次数
    batch_size = 12  # 每个批次的样本数
    learning_rate = 0.05

    train_loss = []  # 训练集损失
    dev_loss = []  # 验证集损失
    train_acc = []  # 训练集正确率
    dev_acc = []  # 验证集正确率

    step = 1

    for epoch in range(iter_time):
        x_train, y_train = shuffle(x_train, y_train)    # 将样本打乱
        for i in range(int(len(x_train)/batch_size)):
            x = x_train[i*batch_size:(i+1)*batch_size]
            y = y_train[i*batch_size:(i+1)*batch_size]
            w_grad, b_grad = gradient(x, y, w, b)
            w = w - learning_rate / np.sqrt(step) * w_grad
            b = b - learning_rate / np.sqrt(step) * b_grad

            step += 1

        y_train_pred = f(x_train, w, b)
        train_acc.append(accuracy(np.round(y_train_pred), y_train))                  # 计算训练集正确率
        train_loss.append(cross_entropy_loss(y_train_pred, y_train) / len(x_train))  # 计算训练集误差

        y_dev_pred = f(x_validation, w, b)
        dev_acc.append(accuracy(np.round(y_dev_pred), y_validation))                        # 计算测试集正确率
        dev_loss.append(cross_entropy_loss(y_dev_pred, y_validation) / len(x_validation))   # 计算测试集误差

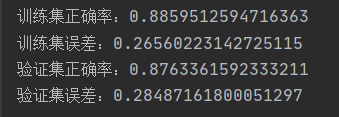
    print('训练集正确率：' + str(train_acc[-1]))
    print('训练集误差：' + str(train_loss[-1]))
    print('验证集正确率：' + str(dev_acc[-1]))
    print('验证集误差：' + str(dev_loss[-1]))

    plt.plot(train_loss)
    plt.plot(dev_loss)
    plt.title('Loss')
    plt.legend(['train', 'dev'])
    plt.savefig('loss.png')
    plt.show()

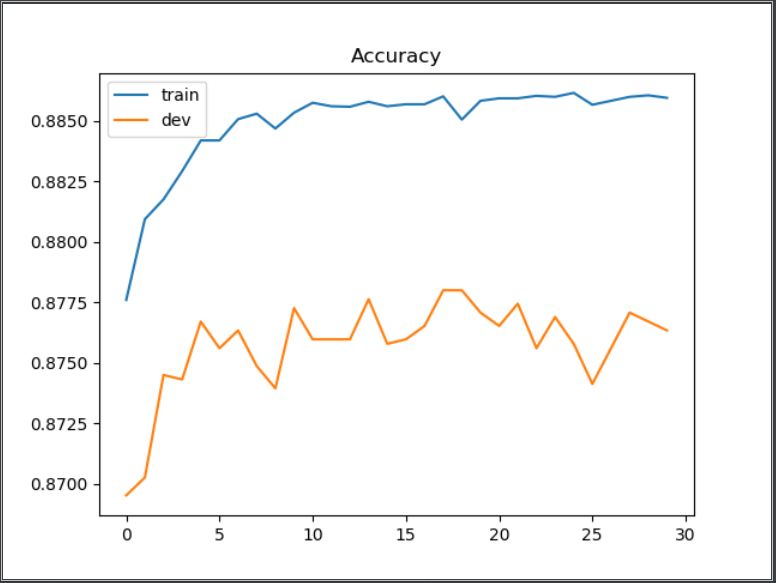
    plt.plot(train_acc)
    plt.plot(dev_acc)
    plt.title('Accuracy')
    plt.legend(['train', 'dev'])
    plt.savefig('acc.png')
    plt.show()

    return w, b

 

测试预测

def predict(x, w, b):
    """预测"""
    result = f(x, w, b)
    result = np.round(result)
    file = open('result.csv', 'w')
    file.write('id,label')
    file.write('\n')
    for i in range(len(result)):
        file.write(str(i) + ',' + str(int(result[i][0])))
        file.write('\n')
    file.close()

 

 

 

 最后去kaggle提交了一下，分数不高。

 

 

完整代码

import pandas as pd
import numpy as np
import math
import matplotlib.pyplot as plt

X_train_file_path = './X_train.csv'
Y_train_file_path = './Y_train.csv'
X_test_file_path = './X_test.csv'


def read_file():
    """读入数据"""
    x_train = pd.read_csv('X_train.csv')
    x_train = x_train.iloc[:, 1:].to_numpy()
    y_train = pd.read_csv('Y_train.csv')
    y_train = y_train.iloc[:, 1:].to_numpy()
    x_test = pd.read_csv('X_test.csv')
    x_test = x_test.iloc[:, 1:].to_numpy()
    # print(x_train.shape)
    # print(y_train.shape)
    # print(x_test.shape)
    return x_train, y_train, x_test


def normalize(X, train=True, X_mean=None, X_std=None):
    """标准化"""
    if train:  # 如果train为True，那么表示处理training
        # data，否则就处理testing data,即不再另算X_mean和X_std
        X_mean = np.mean(X, axis=0).reshape(1, -1)  # 求各列均值
        X_std = np.std(X, axis=0).reshape(1, -1)    # 求各列标准差

    X = (X - X_mean) / (X_std + 1e-8)  # X_std加入一个很小的数防止分母除以0
    return X, X_mean, X_std


def split_data(x_train, y_train, ratio):
    """将数据按ratio比例分成训练集和验证集"""
    x_validation = x_train[math.floor(ratio * len(x_train)):, :]
    y_validation = y_train[math.floor(ratio * len(y_train)):, :]
    x_train = x_train[:math.floor(ratio * len(x_train)), :]
    y_train = y_train[:math.floor(ratio * len(y_train)), :]
    # print(x_train.shape)
    # print(y_train.shape)
    # print(x_validation.shape)
    # print(y_validation.shape)
    return x_train, y_train, x_validation, y_validation


def sigmod(z):
    '''返回sigmod函数'''
    return np.clip(1 / (1.0 + np.exp(-z)), 1e-8, 1-1e-8)   # 避免溢出，如果sigmoid函数的最小值比1e-8小，只会输出1e-8；而比1 - (1e-8)大，则只输出1 - (1e-8)


def f(x, w, b):
    '''返回概率值'''
    return sigmod(np.dot(x, w) + b)


def cross_entropy_loss(y_pred, y):
    """计算误差"""
    loss = -np.dot(y.reshape(1, -1), np.log(y_pred)) - np.dot((1-y).reshape(1, -1), np.log(1-y_pred))
    return loss[0][0]      # 这儿我计算出来就是1×1大小的二维数组


def gradient(x, y, w, b):
    """计算损失函数的梯度"""
    y_pred = f(x, w, b)
    w_grad = np.dot(x.T, y_pred - y)
    b_grad = np.sum(y_pred - y)
    return w_grad, b_grad


def shuffle(x, y):
    """打乱数据"""
    random_list = np.arange(len(x))
    np.random.shuffle(random_list)
    return x[random_list], y[random_list]


def accuracy(y_pred, y):
    """计算正确率"""
    acc = 1-np.mean(np.abs(y_pred - y))
    return acc


def train(x_train, y_train, x_validation, y_validation):
    """批次梯度下降"""
    w = np.ones((x_train.shape[1], 1))
    b = 1
    iter_time = 30   # 迭代次数
    batch_size = 12  # 每个批次的样本数
    learning_rate = 0.05

    train_loss = []  # 训练集损失
    dev_loss = []  # 验证集损失
    train_acc = []  # 训练集正确率
    dev_acc = []  # 验证集正确率

    step = 1

    for epoch in range(iter_time):
        x_train, y_train = shuffle(x_train, y_train)    # 将样本打乱
        for i in range(int(len(x_train)/batch_size)):
            x = x_train[i*batch_size:(i+1)*batch_size]
            y = y_train[i*batch_size:(i+1)*batch_size]
            w_grad, b_grad = gradient(x, y, w, b)
            w = w - learning_rate / np.sqrt(step) * w_grad
            b = b - learning_rate / np.sqrt(step) * b_grad

            step += 1

        y_train_pred = f(x_train, w, b)
        train_acc.append(accuracy(np.round(y_train_pred), y_train))                  # 计算训练集正确率
        train_loss.append(cross_entropy_loss(y_train_pred, y_train) / len(x_train))  # 计算训练集误差

        y_dev_pred = f(x_validation, w, b)
        dev_acc.append(accuracy(np.round(y_dev_pred), y_validation))                        # 计算测试集正确率
        dev_loss.append(cross_entropy_loss(y_dev_pred, y_validation) / len(x_validation))   # 计算测试集误差

    print('训练集正确率：' + str(train_acc[-1]))
    print('训练集误差：' + str(train_loss[-1]))
    print('验证集正确率：' + str(dev_acc[-1]))
    print('验证集误差：' + str(dev_loss[-1]))

    plt.plot(train_loss)
    plt.plot(dev_loss)
    plt.title('Loss')
    plt.legend(['train', 'dev'])
    plt.savefig('loss.png')
    plt.show()

    plt.plot(train_acc)
    plt.plot(dev_acc)
    plt.title('Accuracy')
    plt.legend(['train', 'dev'])
    plt.savefig('acc.png')
    plt.show()

    return w, b


def predict(x, w, b):
    """预测"""
    result = f(x, w, b)
    result = np.round(result)
    file = open('result.csv', 'w')
    file.write('id,label')
    file.write('\n')
    for i in range(len(result)):
        file.write(str(i) + ',' + str(int(result[i][0])))
        file.write('\n')
    file.close()


if __name__ == '__main__':
    x_train, y_train, x_test = read_file()
    x_train, x_mean, x_std = normalize(x_train)
    x_train, y_train, x_validation, y_validation = split_data(x_train, y_train, 0.9)
    w, b = train(x_train, y_train, x_validation, y_validation)
    x_test, x_mean, x_std = normalize(x_test   # 对测试数据进行标准化
    predict(x_test, w, b)