树上背包

处理存在树结构的依赖关系的背包问题。

• P2014 [CTSC1997] 选课

建出依赖关系的树，显然有一个 \(O(n m^2)\) 的 dp：设 \(f_{u, i}\) 表示考虑以 \(u\) 为根的子树，占用了 \(i\) 的重量所得到的最大价值。直接枚举子节点并转移即可。

使用上下界优化，即对于枚举子节点的过程，我们枚举占用的总重量时，上界为 \(\min\{m, \text{sz}_u\}\)，同理，枚举以子节点 \(v\) 为根的子树占用的重量时，上界也与 \(\text{sz}_v\) 取 \(\min\)。（其中 \(\text{sz}_i\) 表示以 \(i\) 为根的子树的大小）。

考虑分析使用该优化后的时间复杂度。

首先一个宽松的上界是 \(O(n m^2)\)，接下来我们分情况讨论：

1. \(n < m\)
   此时，考虑每个节点 \(u\) 对复杂度的贡献，我们知道树上背包的过程是顺序枚举子节点 \(v\)，并考虑 \(v\) 与之前的所有点的贡献。容易发现该贡献与“顺序枚举 \(v\)，直接计算 \(v\) 与其他儿子节点的贡献”得到的结果同阶。
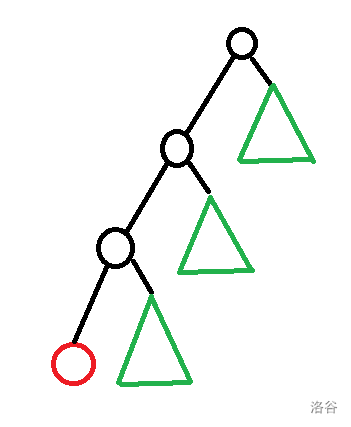
   故复杂度为 \(\sum\limits_{1 \le u \le n} \sum\limits_{v \in \text{son}_u} \text{sz}_v \times (\text{sz}_u - \text{sz}_v - 1)\)。则对于原树上的每个节点，能与它产生贡献的节点形如：
   
   其中红色点为当前考虑的节点，绿色部分为可以与红点产生贡献的节点。
   易得绿色部分的大小是 \(O(n)\) 的。因此复杂度上界为 \(O(n^2)\)。
2. \(n \ge m\)
   为方便描述，我们将节点 \(u\) 的多个子节点合并后的点集也定义为“子树”。
   此时，复杂度贡献仍可以分为三个部分：
   1. 大小小于 \(m\) 的子树之间的贡献
      直接按照 \(n < m\) 的方式分析即可。此时，对于点 \(u\)，最后一次有贡献时它与它所在的子树与造成贡献的子树的大小都小于 \(m\)，故贡献为 \(O(m)\)，总贡献为 \(O(nm)\)。
   2. 大小不小于 \(m\) 的子树与大小小于 \(m\) 的子树之间的贡献
      首先我们有结论：子树 \(A\) 对子树 \(B\) 的贡献，与子树 \(B\) 对子树 \(A\) 的贡献相等。于是考虑大小小于 \(m\) 的子树受到的贡献。
      仍然枚举每个节点 \(u\)，考虑 \(u\) 受到的贡献。我们发现 \(u\) 最多只会与一棵子树产生贡献，因为贡献产生后得到的新子树大小必定大于 \(m\)。而一次贡献为 \(O(m)\)，故总贡献为 \(O(nm)\)。
   3. 大小不小于 \(m\) 的子树之间的贡献。
      首先大小不小于 \(m\) 的子树的贡献等价于大小等价于 \(m\) 的子树的贡献。
      接着考虑如下分摊贡献的方式：若某一时刻，某子树的大小达到了 \(m\)，则从其中选 \(m\) 个点作为可以产生贡献的点。合并两棵子树 \(A\) 与 \(B\) 时，计算 \(A\) 中可以受到贡献的点的贡献，并将这些点标记为不可以受到贡献。
      在这种分摊贡献的方式下，每个点最多只会受到一次 \(m\) 的贡献，因此总贡献不超过 \(O(nm)\)。

综上，上下界优化后的树上背包的复杂度为 \(O(n \times \min\{n, m\})\)。

• LOJ160 树形背包

与上一道题的区别是每个点的重量可能不为 \(1\)。这时上下界优化就不奏效了（容易通过复杂度分析得），考虑如下做法：

对于原树的后序遍历，从前向后考虑，\(f_{i, j}\) 表示考虑了后序遍历中的前 \(i\) 个点，选出的点的重量之和为 \(j\) 的最大价值。显然，若选了第 \(i\) 个点，则贡献为 \(f_{i - 1, j - w_i} + v_i\)；否则，贡献为 \(f_{i - \text{sz}_i, j}\)。易得该做法的复杂度为 \(O(nm)\)。

不过该做法的一个小缺点是无法直接得到任意一个子树的状态。如果真的会多次询问不同子树的状态，可以考虑 dsu on tree 维护最基础的 dp，复杂度为 \(O(m^2 \log n)\)。