【图论】tarjan

注意：这篇文章是超级远古的时候写的，只是应同学要求搬过来，以后不做修改。

On 2024.10.25 本文内容有大量细节错误，作者现在没有时间修，所以如果读起来觉得有问题，请先自行思考一下qwq

什么是强连通分量 \(scc\) ？

算法竞赛是很讲究效率的。

我们知道，对于一般的图，我们可以将每一个节点视为最小单位。

但，某些时候，当一个子图中的任意两个点都可以互相到达后，我们就可以将其看做一个“点”了。

举例：

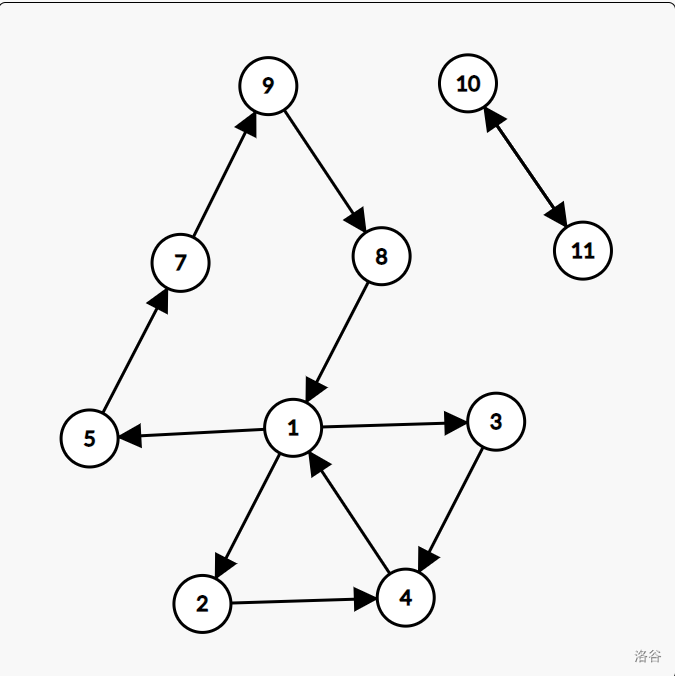
很明显，此图中的 \(1 \sim 9\) 号点、\(10 \sim 11\) 号点之间都能互相到达，那么有些时候，我们就可以将其压缩成两个点。这样的话，做起题来就更为简便了。

总结一下：强连通分量是满足“任意两节点都能相互到达”这一条件的 最大子图 ，我们一般称之为 \(scc\) 。

---

前置概念

• 关于节点的基本概念

对于上附图，它的结构非常复杂，于是，我们就可以把它简化。

怎样简化呢？首先，我们忽略图中大部分的边，仅仅保留图的 \(dfs\) 序。

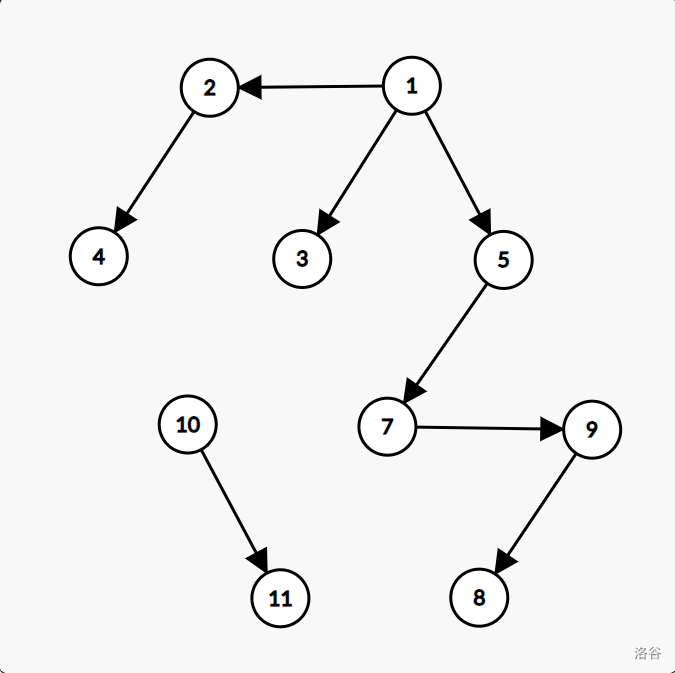
显然，最后原先的图就变成了一个森林。

经过处理后，原先的节点并不一定能保留它原先在图中的位置。为了在森林中更好地处理每个节点的信息，我们选择保留每个节点的 \(dfs\) 序。

我们习惯性地将 \(dfs\) 序称作 时间戳 。它的名称是 \(dfn\) 。\(dfn_i\) 代表第 \(i\) 个节点的时间戳。

示例：

对于上图，经处理后的图是这样子的：

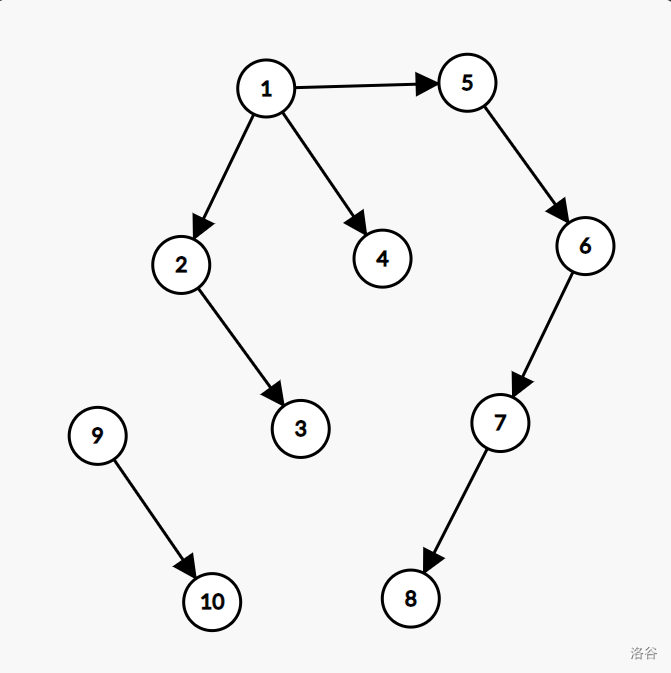
\(note ：\) 图中的编号代表时间戳

现在，我们就能轻松地在图上进行操作了。

我们知道，对于一个点，要是它能到达一个在它之前的点，那它很有可能就在一个强连通分量里。

由此可以看出 \(：\) 一个点能到达的最小时间戳对于强连通分量问题来说非常地重要。我们一般称 一个点能到达的最小时间戳 为 追溯值 ，它的名称是 \(low\) 。\(low_i\) 代表第 \(i\) 个节点的追溯值。

由此，我们就可以了解 \(Tarjan\) 所需的，关于点的基本概念了。

• 关于边的基本概念

我们虽然有了一个简化后的图，但曾经存在的边还是要加的。我们一般把边分为以下四类：

1. 树边

我们一开始建的森林，它里面的边全都是树边。

树边，是最先加入的边

树边的性质：树边是构成整个图的基石

举例：

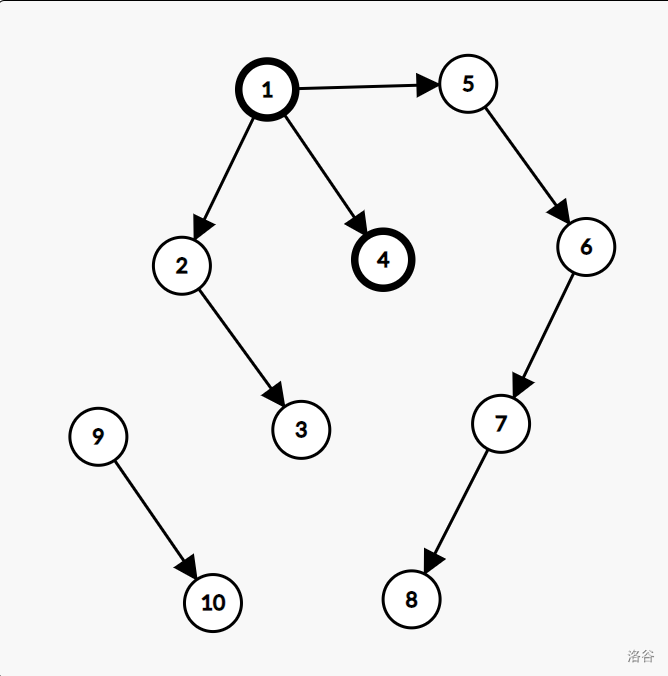
此图中，加粗的两点 \(1,4\) 之间的边即是树边。

2. 返祖边（回边）

返祖边，即是回到祖先节点的边

返祖边的性质：只要出现返祖边，就一定有强连通

很好理解罢

注意：这个强连通并不一定是强连通分量。

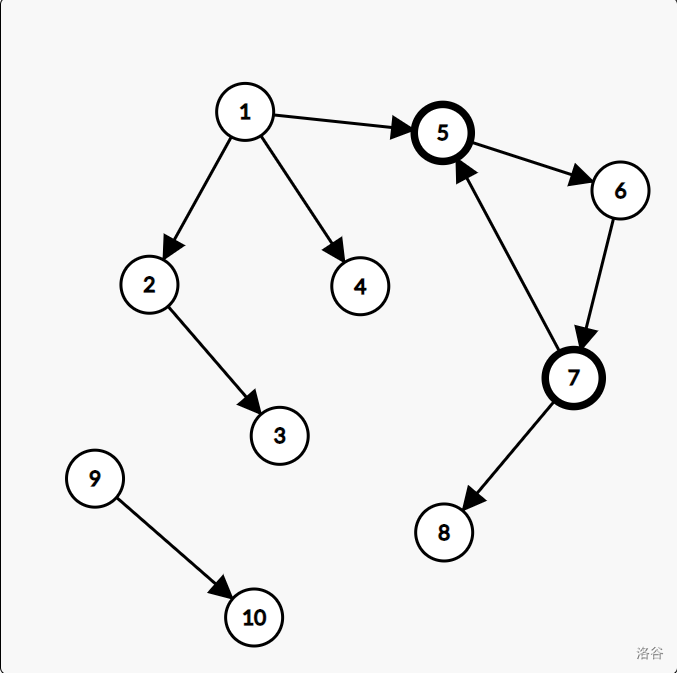
此图中，从 \(7\) 号点连到 \(5\) 号点的边即为一条返祖边。

此时，由于返祖边的出现，\(5,6,7\) 三个点可以被认为组成了一个强连通。

3. 横叉边

横叉边，即是从一颗子树连接到另一颗子树的边。

横叉边的性质：无

注：“无”的意思是，一旦出现了一条横叉边，那它可能意味着强连通，也可能是一条废边。

横叉边举例：

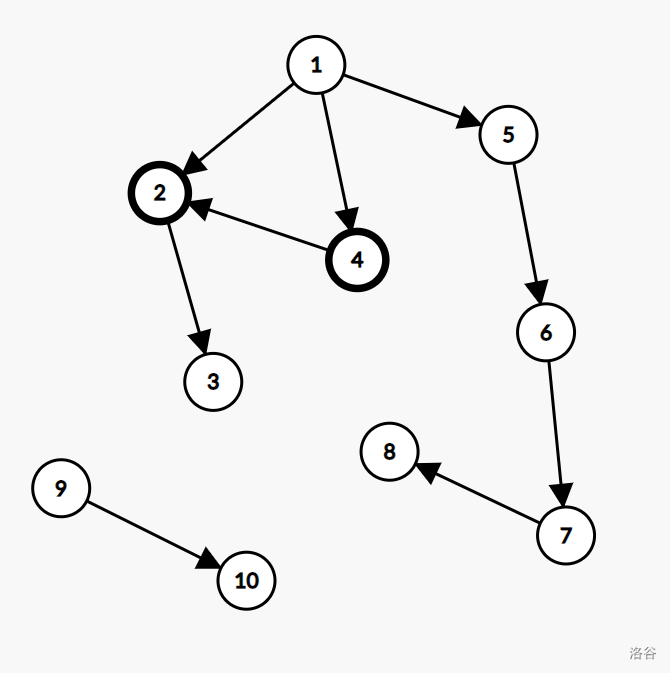
此图中，\(4\) 号点到 \(2\) 号点的边即是一条横叉边

4. 前向边

前向边，即是跨越了儿子节点，连向其余的子孙节点的边

前向边的性质：前向边是废边（

废边这个应该很好理解罢，向本来就能走到的子节点连了一条边，并不能改变这个子节点原本就能被到达，以及目前并没有产生新的强连通分量的事实。

举例：

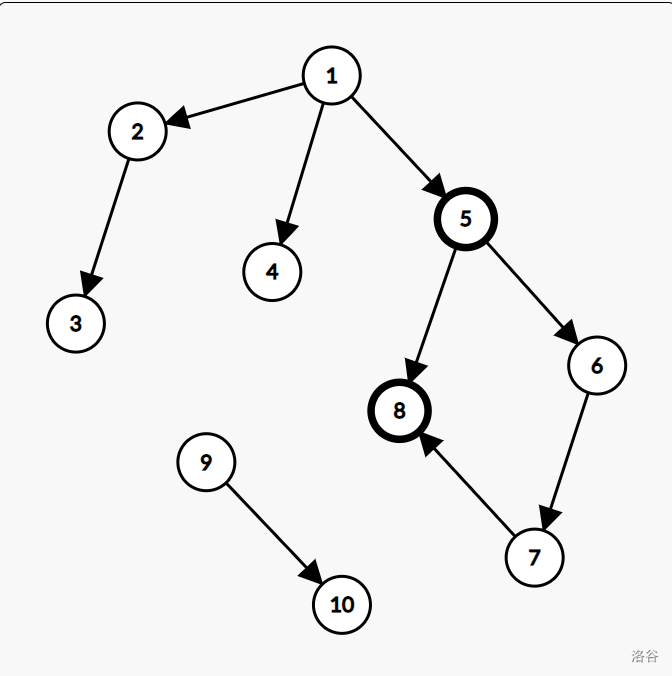
此图中，由 \(5\) 号点连向 \(8\) 号点的边即是一条前向边。

注意：这条前向边必定是在 \(5\) 到 \(6 ,\) \(6\) 到 \(7\) 等等这些边连完之后再连的。这个可以体会一下：要是不这样的话那 \(5\) 到 \(8\) 这条边就变成一条树边了（

---

给几个关于边容易犯的错误吧：

1. 如下图，这种不在同一层上的边是什么边？

注：所描述的边为：从 \(4\) 到 \(3\) 的边。

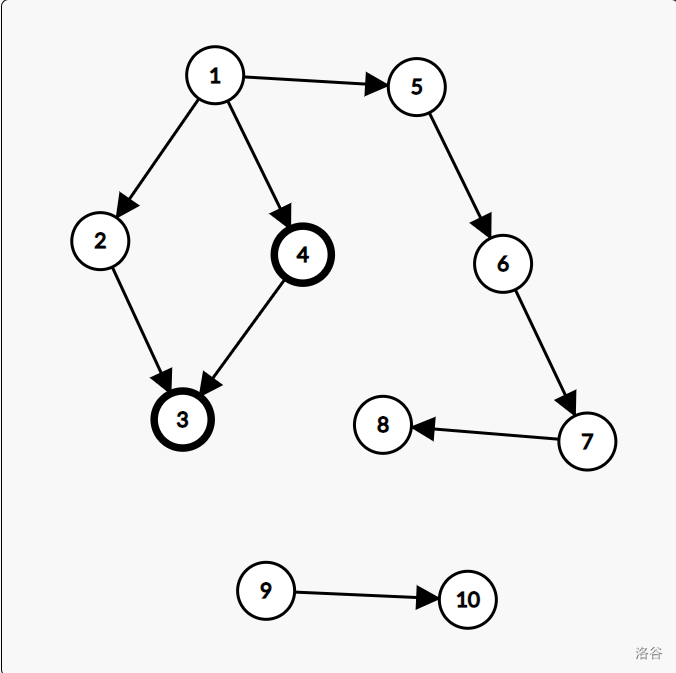
根据定义，不用多想，是横叉边（

2. 如下图，这种从前一颗子树连到后一颗子树的边是什么边？

注：所描述的边为：从 \(2\) 到 \(4\) 的边。

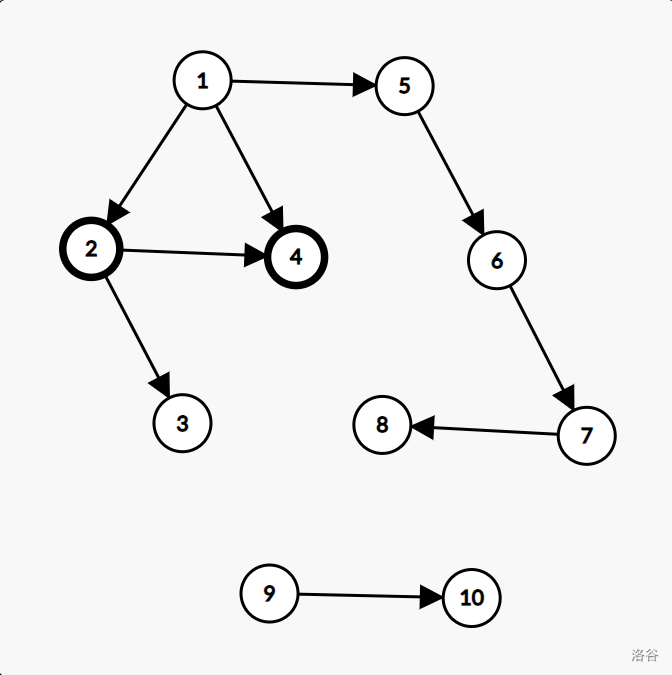
这种边经常会被误认为是横叉边，其实不然。因为在遍历到 \(2\) 时，肯定会延此边顺序遍历至 \(4\) 。

换句话说，一旦有这条边的话，此图是这样的：

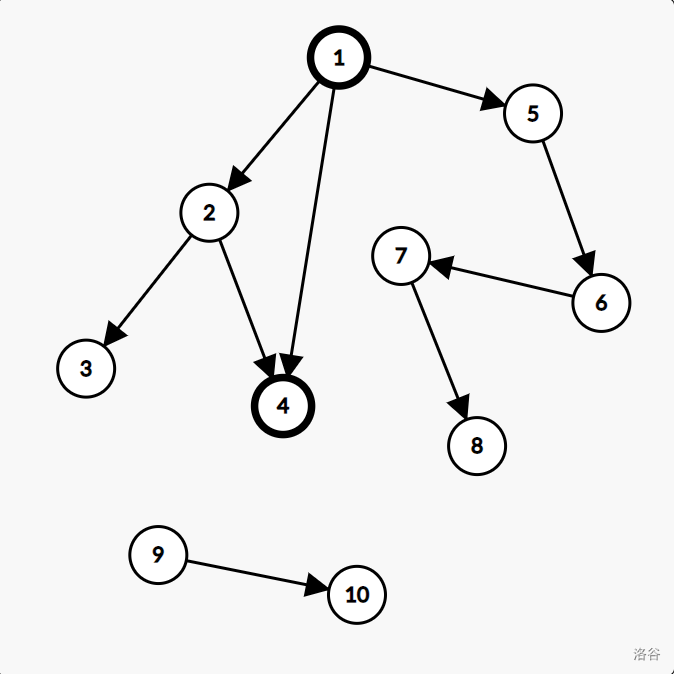
显然，这条边本质上是一条树边，而原本从 \(1\) 到 \(4\) 的边则变成了一条前向边。

---

搞明白了前置芝士，我们再来康康 \(Tarjan\) 求强连通分量的思路。

\(Tarjan\) 的思想

\(Tarjan\) 算法利用了一个事实：在我们新构造的图中，对于每一个强连通分量 \(scc\) ，它必定对应且仅对应在这个 \(scc\) 中的一个点，使得这个点的 \(dfn\) 值等于 \(low\) 值且这个点的 \(dfn\) 值一定是 \(scc\) 里的所有 \(dfn\) 中最小的一个。

\(Q:\) 为什么有且仅有这样的一个点？

\(A:\) 因为 \(scc\) 中必定存在环。而环中必定存在着这样的一个点。

\(Q:\) 为什么这个点的 \(dfn\) 一定最小？

\(A:\) 因为我们是按照 \(dfs\) 序来遍历这个图的，而一旦这个点的 \(dfn\) 值并不是最小的，就一定意味着它可以通过某条路径返祖，与第一条事实相违背。

那么，\(Tarjan\) 算法是如何利用这个事实的呢？

首先，我们照常地 \(dfs\) 整个图并更新 \(low,dfn\) 等。

其次，一旦发现一个点 \(i\) 使得 \(dfn_i = low_i\) ，就记录一次强连通分量。

利用第二个性质，这个 \(scc\) 里的点的 \(dfn\) 值都必定大于等于 \(dfn_i\) ，于是我们可以用一个栈来记录所有已遍历过的边。每一次都从栈顶开始弹出所有 \(dfn\) 值大于等于 \(dfn_i\) 的点并将其记录。这样，我们就可以不重不漏地寻找出所有的强连通分量了。

\(Tarjan\) 的时间复杂度

显然，在 \(Tarjan\) 过程中每个点都只遍历了常数次，每条边也都只遍历了常数次，所以其复杂度为 \(O(n+m)\) 。

\(Tarjan\) 中经典的优化

通过对边的分析，我们知道类似于前向边这种边是没有用处的，那么我们如何处理掉这些废边呢？

我们可以使用一个数组 \(vis\) 来标记 \(scc\) 是否已经确定。简单来说，\(vis_i\) 表示编号为 \(i\) 的点所在的 \(scc\) 是否已经确定。

一般来说，对于一个点 \(i\) ，\(vis_i = 0\) 代表这个点的 \(scc\) 已确定或这个点还未被遍历到。\(vis_i = 1\) 则代表这个点已经被搜索到，但其 \(scc\) 还未确定。

我们可以在 \(dfs\) 到一个点时给这个点的 \(vis\) 打上标记，在这个点的 \(scc\) 确定时再将它的 \(vis\) 还原。

有了这个数组，我们就好判断多了：对于一条边，只要它的 \(vis\) 值为 \(1\) ，即它的 \(scc\) 还未确定，那么我们就不用搜索它了。因为我们目前所在的这个点的 \(scc\) 也是还未确定的，也就是说，目前的点与这条边的终点是有路径关系的，因此，即使再对终点进行搜索，也只会多走路径。因此，这条边存在的价值就仅限于更新 \(low_u\) ，同时，我们也避免了陷入死循环。

有了如上的分析，我们对 \(Tarjan\) 的写法就清晰多了。

\(Tarjan\) 模板

//#pragma GCC optimize (2)
#include <bits/stdc++.h>
#define int long long

using namespace std;
const int N = 1e4 + 5;
const int M = 5e4 + 5;

int n, m, cnt;
int head[N];
// 从此以下皆为寻找 scc 所需的变量
int vis[N], low[N], dfn[N];
int scc[N]; 	// scc[i] 代表点 i 所对应的 scc 的编号
int scc_count, pnt;	// scc_count 记录 scc 的数量，pnt （point）用来更新节点的 dfn
stack <int> st;	// st 为我们所说的栈
// 从此以上皆为寻找 scc 所需的变量
struct node {
	int nxt, u, v;
};
node a[M];

void add (int x, int y) {
	// 这部分是纯纯的板子，在这里不随题目的变化而变化
	a[ ++ cnt].nxt = head[x];
	a[cnt].u = x;
	a[cnt].v = y;
	head[x] = cnt;
}

void tarjan (int u) {
	// tarjan 模板，参数 u 为目前搜索到的点
	vis[u] = 1, low[u] = dfn[u] = ++ pnt;
	st.push (u);
	// 初始化，别忘记将 u 放入栈中
	for (int i = head[u]; i; i = a[i].nxt) {
		// 遍历所有的边
		int v = a[i].v;
		if (!dfn[v]) {
			// 如果一条边的终点没被搜索过，就对它进行搜索，并将 low[u] 赋值为 low[u] 和 low[v] 的最小值，即：u 目前能到达的最小点是“u 曾经能到达的最小点”和“v 能到达的最小点”中最小的点（
			tarjan (v);
			low[u] = min (low[u], low[v]);
		} else if (vis[v]) {
			// 如果 vis[v] 为一，则代表该点的 scc 未确定
			low[u] = min (low[u], dfn[v]);
			// 这里写 dfn[v] 或 low[v] 都行，毕竟只是打个标记，不论如何都不影响后面的操作，毕竟要是 u 并不是我们所要寻找的那种点那这一步肯定能更新掉的
        	// 但是在求割点等情况下只能写 dfn[v] 呢qwq ，所以以后还是用 dfn[v] 吧
		}
	}
	
	if (low[u] == dfn[u]) {
		// 一旦这个点是要找的，那就求出它所在的 scc 中的所有点
		// 下面的代码应该比较好理解罢
		++ scc_count;
		while (!st.empty () && dfn[st.top ()] >= dfn[u]) {
			int k = st.top ();
			scc[k] = scc_count;
			vis[k] = 0;
			// 给自己的小提示：这里 vis 必须写到 while 里面！毕竟按照定义来就是该且只能写到这儿的
			st.pop ();
		}
	}
}

signed main () {
	scanf ("%lld%lld", &n, &m);
	for (int i = 1; i <= m; i ++ ) {
		int u, v;
		scanf ("%lld%lld", &u, &v);
		add (u, v);
	}
	
	for (int i = 1; i <= n; i ++ )	// 要是这个图不连通怎么办？所以我们要对每一个需要 tarjan 的点都进行 tarjan ！
		if (!dfn[i])
			tarjan (i);
	
	for (int i = 1; i <= n; i ++ )
		printf ("%lld ", scc[i]);
	puts ("");
	
	return 0;
}

样例输入：

10 12
1 2
2 4
4 1
1 3
3 4
1 5
5 6
6 8
8 7
7 1
9 10
10 9

样例输出：

1 1 1 1 1 1 1 1 2 2

---

经典例题

洛谷 P2863 [USACO06JAN]The Cow Prom S

题目分析：

裸的求强连通分量。唯一的更改仅仅是需要记录 \(scc\) 里点的个数并进行判断。题目过于简单，因此这里不再给出代码。

洛谷 P3387 【模板】缩点

题目分析：

显然在这个图里的强连通分量之间都可以互相到达，那么我们可以将一个 \(scc\) 缩为一个点。

在得到一张被缩完的图后，我们就可以进行 \(dp\) 了。

首先，现在的图必定是一个有向无环图 \(DAG\) 。那么，我们可以建立数组 \(f\) 以进行 \(dp\) 。\(f_i\) 表示截止到第 \(i\) 个点能走过的最大权值。为了保证图的有序性，我们可以先对其进行拓扑排序 \(topo\) ，再顺序遍历每一个节点。对于每一个节点 \(v\) ，其权值为 \(f_v\) 和 \(tmp_v + f_u\) 的最大值。

最后，在所有的 \(f_i\) 中寻找最大的一个，输出即可。

P3388 【模板】割点（割顶）

\(note:\) 模板题

1. 什么是割点？

在一个无向图中，存在着一种点。设点 \(i\) 为其中的一个，则一旦删去点 \(i\) ，无向图的连通块会增加。我们称这种点为 割点 。

2. 如何求割点？

考虑在一个 \(dfs\) 图中，当我们枚举点 \(u\) 时。一旦 \(u\) 为割点，则意味着点 \(u\) 必定满足对于每一个子节点 \(v\) ，都有 \(low_v \ge dfn_u\) 。用人话来说即 \(v\) 能到达的节点的 \(dfn\) 最小值大于等于 \(u\) ，这说明 \(v\) 无法回到 \(u\) 的祖先节点，那么 \(u\) 就是割点了。

但这里，我们要考虑一种特殊情况：根节点。

为什么我们要特判根节点呢？因为根节点是没有祖先节点的，那么我们上面的分析就不成立了。

那么如何判断根节点是否为割点呢？显然，一旦根节点是割点，那它就必定至少有两个不相交的子树。那么，我们只需要判断它的子树数量就可以了。

由于求割点与求强连通分量不同，所以此时我们并不需要栈存储节点等操作。

接着，就是我们上文提到过的问题：\(tarjan\) 中有一段很迷惑的代码：

low[u] = min (low[u], dfn[v]);

为什么这里要写 \(dfn_v\) ，而非 \(low_v\) 呢？

1. \(low_v\) 为什么不成立？

   我们知道，回溯值的定义是一个点能到达的，时间戳最小的点的时间戳。

   但这个定义，在求割点的时候就会出现问题：整张图的边都是无向的，所以一旦写成了 \(low_v\) ，所有节点的回溯值就会被更新为根节点的时间戳。

2. \(dfn_v\) 为什么正确？

   考虑点 \(v\) 与当前节点 \(u\) 的关系。

   如果通过 \(v\) 是 \(u\) 的祖先节点，那不管 \(v\) 是那个点，\(u\) 的回溯值都会被更新，使得其小于 \(u\) 的时间戳。

   如果 \(v\) 不是 \(u\) 的祖先，但通过 \(v\) 可以到达 \(u\) 的祖先，那因为此时 \(v\) 已经被遍历过了（\(dfn_v\) 不为 \(0\)），所以先前遍历到 \(v\) 时，一定可以通过某条路径遍历到 \(u\) ，因此 \(u\) 就成为了 \(v\) 的子孙节点，又回到了第一种情况。

   如果 \(v\) 既不是 \(u\) 的祖先，也无法通过某条路径连接到 \(u\) 的祖先，那不管写 \(dfn_v\) ，还是写 \(low_v\) ，效果都是一样的，因此 \(dfn_v\) 不影响正确性。

模板：

//#pragma GCC optimize (2)
#include <bits/stdc++.h>
#define int long long

using namespace std;
const int N = 1e5 + 5;
const int M = 5e5 + 5;

int n, m;
int low[N], dfn[N], head[N];
int scc[N];
int cnt, ans, scc_count, pnt;
struct node {
	int nxt, u, v;
};
node a[M];
int ans_pnt[N];	// 记录一个点是否为割点。设 ans_pnt[i] = 1 ，则 i 号点为割点
int rt;	// rt 标记根节点

void add (int x, int y) {
    a[ ++ cnt].nxt = head[x];
    a[cnt].u = x;
    a[cnt].v = y;
    head[x] = cnt;
}

void tarjan (int u) {
	low[u] = dfn[u] = ++ pnt;
	int son = 0;	// son 记录子树个数
	for (int i = head[u]; i; i = a[i].nxt) {
		int v = a[i].v;
		if (!dfn[v]) {
			son ++ ;	// v 号点没被标记过，则代表目前没有别的到 v 号点的路径，则 v 号点对应着一个新的子树
			tarjan (v);
			low[u] = min (low[u], low[v]);
			if (low[v] >= dfn[u] && u != rt && !ans_pnt[u])	// 若 low[v] >= dfn[u] 且 u 并不是根节点且 u 没被标记过，则进行标记
				ans ++ , ans_pnt[u] = 1;
		} else {
			low[u] = min (low[u], dfn[v]);
		}
	}
	
	if (son > 1 && u == rt && !ans_pnt[u])	// 特判根节点
		ans ++ , ans_pnt[u] = 1;
}

signed main () {
	scanf ("%lld%lld", &n, &m);
	for (int i = 1; i <= m; i ++ ) {
		int u, v;
		scanf ("%lld%lld", &u, &v);
		add (u, v), add (v, u);	// 无向图两次建边
	}
	
	for (int i = 1; i <= n; i ++ )
		if (!dfn[i])
			rt = i, tarjan (i);	// 别忘了标记 rt
	
	printf ("%lld\n", ans);
	for (int i = 1; i <= n; i ++ )
		if (ans_pnt[i])	printf ("%lld ", i);
	puts ("");
	
	return 0;
}

洛谷 P1656 炸铁路

\(note:\) 模板题

1. 什么是割边？

类似于割点，即无向图中的一些边。设边 \(i\) 是一条割边，则一旦将割边删除，则无向图的连通块数量增加。

2. 如何求割边？

与割点类似。

考虑到，一旦一个边是割边，则将它删除后，它的终点必定无法返祖，即 \(low_v > dfn_u\) 。

为什么呢？因为一旦 \(low_v \le dfn_u\) ，则意味着从 \(v\) 出发，不通过割边也能走到祖先节点。也就是说即使将这条边删掉，连通块数量仍然不变，与割边定义不符，故证明完毕。

有了割点的铺垫，割边就好写多了。

模板：

//#pragma GCC optimize (2)
#include <bits/stdc++.h>
#define int long long

using namespace std;
const int N = 1e3 + 5;
const int M = 1e4 + 5;

int n, m, pnt, cnt, cnt2;
int dfn[N], low[N], head[N];
int fa[N];	// 在无向图中，标记是否为父亲 
struct node {
	int u, v;
	int nxt;
};
node a[M], Edge[M];	// Edge 存割边

void add (int x, int y) {
	a[ ++ cnt].nxt = head[x];
	a[cnt].u = x;
	a[cnt].v = y;
	head[x] = cnt;
}

void addEdge (int x, int y) {
	// 这里就不用那么麻烦的加边操作了
	Edge[ ++ cnt2].u = min (x, y);
	Edge[cnt2].v = max (x, y);
	// min / max 是为了保证边的内部顺序
}

void tarjan (int u) {
	dfn[u] = low[u] = ++ pnt;
	for (int i = head[u]; i; i = a[i].nxt) {
		int v = a[i].v;
		if (!dfn[v]) {
			fa[v] = u;	// 标记父亲，因为不能走到父亲 
			tarjan (v);
			low[u] = min (low[u], low[v]);
			if (low[v] > dfn[u]) {
				// 找到割边了
				addEdge (u, v);
			}
		} else if (v != fa[u]) {
			low[u] = min (low[u], dfn[v]);
		}
	}
}

bool cmp (node x, node y) {
	// 排序函数，用来将边排序输出
	if (x.u < y.u)	return true;
	else if (x.u == y.u && x.v < y.v)	return true;
	else	return false;
}

signed main () {
	scanf ("%lld%lld", &n, &m);
	for (int i = 1; i <= m; i ++ ) {
		int u, v;
		scanf ("%lld%lld", &u, &v);
		add (u, v), add (v, u);
	}
	
	for (int i = 1; i <= n; i ++ )
		if (!dfn[i])
			tarjan (i);
	
	sort (Edge + 1, Edge + cnt2 + 1, cmp);
	
	for (int i = 1; i <= cnt2; i ++ )
		printf ("%lld %lld\n", Edge[i].u, Edge[i].v);
	
	return 0;
}

洛谷 P8435 【模板】点双连通分量

\(note:\) 模板题

1. 什么是点双连通分量 \(DCC\) ？

在无向图中，存在着一种子图 \(G\) ，使得对于任意节点 \(i \in G\) ，在将 \(i\) 删除后， \(G\) 仍然连通。我们一般将这样的最大子图成为点双连通分量 \(DCC\) 。

注：单独的一个点，即孤立点，自成一个 \(DCC\) 。

2. 如何求点双？

首先，注意到这样一个引理：两个点双的公共点必定是割点。

为什么呢？因为一旦将公共点删去，两个点双之间必定无法互相到达。进而推出，公共点满足割点的性质，即公共点是割点。

进而推出：一个点双的边界必定是割点。

这又是怎么来的呢？

首先，设边界并非为割点，则对于本应为边界的割点来说，点双里的任意一点，都必定有大于 \(1\) 种方法到达割点，否则，就会出现新的割点了，与前提矛盾。

至于有没有可能出现其中的一条路径是通过非点双里的点到达的呢？由于无向图中只可能存在树边和前向边，易证得：若存在通过祖先到达的情况，则这个祖先也必定属于点双。故推出假设错误。

而假设隔着割点又新加入了节点，则必定有不通过割点到达新点的路径，与假设矛盾。

于是，我们就可以总结出求点双的方法了：

1. \(tarjan\) 遍历所有点。

2. 与求强连通分量类似，我们使用一个栈 \(st\) 存储节点。

3. 一旦遇到割点，则将栈内所有 \(dfn\) 比割点的 \(dfn\) 大的节点，包括割点，全部记录，并将点双中除割点外的点弹出。

注意：

1. 记录的点，就相当于一颗以割点为根的子树。

2. 为什么不弹出割点？因为割点还有可能被包含在以它为叶子节点的点双中。

最后，提醒一下：孤立点也是点双，需要特判！

模板：

//#pragma GCC optimize (2)
#include <bits/stdc++.h>
#define int long long

using namespace std;
const int N = 5e5 + 5;
const int M = 4e6 + 5;

int n, m;
int low[N], dfn[N], head[N];
int cnt, pnt, top;	// top 记录栈顶 
struct node {
	int nxt, u, v;
};
node a[M];
int fa[N], st[N];
// fa 存储父亲节点，fa[i] 存储 i 号点的父节点。该数组用来特判孤立点，同时，在遍历的时候还可以用它防止走回父节点的情况发生。
// st 为手写栈，注意：这里因为图有可能是森林，所以我们要多次清空栈，故可以使用此时相对方便的手写栈 
int dcc;
vector <int> dcc_pnt[N];
// dcc 记录点双个数，dcc_pnt 存储每个点双里的点 

void add (int x, int y) {
    a[ ++ cnt].nxt = head[x];
    a[cnt].u = x;
    a[cnt].v = y;
    head[x] = cnt;
}

void tarjan (int u) {
	st[ ++ top] = u;
	low[u] = dfn[u] = ++ pnt;
	int son = 0;
	//初始化，son 记录儿子节点的个数用来特判孤立点 
	for (int i = head[u]; i; i = a[i].nxt) {
		int v = a[i].v;
		if (!dfn[v]) {
			son ++ ;
			fa[v] = u, tarjan (v);
			low[u] = min (low[u], low[v]);
			if (low[v] >= dfn[u]) {	// 意味着 u 为割点且找到了新的子树，故添加新的点双
				// 注意这里和强连通分量的 tarjan 不一样 
				dcc ++ ;
				dcc_pnt[dcc].push_back (u);
				while (top > 0 && dfn[st[top]] >= dfn[v])	dcc_pnt[dcc].push_back (st[top]), top -- ;
			}
		} else if (v != fa[u]) {
			// 不能走回父节点，所以要判断 
			low[u] = min (low[u], dfn[v]);
		}
	}
	
	if (fa[u] == 0 && son == 0)	dcc_pnt[ ++ dcc].push_back (u);
	// 特判孤立点 
}

signed main () {
	scanf ("%lld%lld", &n, 	&m);
	for (int i = 1; i <= m; i ++ ) {
		int u, v;
		scanf ("%lld%lld", &u, &v);
		if (u != v)	add (u, v), add (v, u);
	}
	
	for (int i = 1; i <= n; i ++ )
		if (!dfn[i]) {
			top = 0;	// 初始化栈顶 
			tarjan (i);
		}
	
	printf ("%lld\n", dcc);
	for (int i = 1; i <= dcc; i ++ ) {
		printf ("%lld ", dcc_pnt[i].size ());
		for (int j = 0; j < dcc_pnt[i].size (); j ++ )	printf ("%lld ", dcc_pnt[i][j]);
		puts ("");
	}
	
	return 0;
}

洛谷 P8436 【模板】边双连通分量

\(note:\) 模板题

1. 什么是边双连通分量 \(BCC\) ？

在无向图中，存在着一种子图 \(G'\) ，与点双类似，使得对于任意边 \(j \in G'\) ，在将 \(j\) 删除后，\(G'\) 仍然连通。我们一般将这样的最大子图成为边双联通分量 \(BCC\) 。

2. 如何求边双？

首先，割边必定不属于任何边双，因为将它删除会导致整张图不连通。

其次，注意到边的性质：将割边删除并不会导致边双不连通，或割边变为普通边。

上面的这一条可以理解一下。

通过这两条性质，易得出边双的求法：

将所有割边删除，剩下的连通块就是边双。

为什么呢？首先，将割边删除这一步很好理解，其次，剩下的连通块中必定不含有割边，由此退出剩下的连通块为边双，因为边双，就是一张不含割边的图。

相较于点双，边双就简单多了。

模板：

//#pragma GCC optimize (2)
#include <bits/stdc++.h>
#define int long long

using namespace std;
const int N = 5e5 + 5;
const int M = 4e6 + 5;

int n, m;
int cnt, pnt;
int head[N], dfn[N], low[N], fa[N];
// 与点双中的 fa 相同，这里的 fa 记录父节点。不同的是，这里的 fa 少了判断孤立点的功能，因为孤立点不用考虑 
struct node {
    int u, v;
    int nxt;
};
node a[M];
bool vis1[N], vis2[M];
// vis1 在求连通块的过程中标记走过的点，vis2 标记割边 
int bcc;
vector <int> bcc_pnt[N];
// bcc 记录边双个数，bcc_pnt 存储边双里的节点 

void add (int x, int y) {
    a[cnt].nxt = head[x];
    a[cnt].u = x;
    a[cnt].v = y;
    head[x] = cnt ++ ;
    // 注意，无向图中割边要标记两次。我们使用位运算进行标记，故要求边从 0 开始计数 
}

void tarjan (int u) {
    dfn[u] = low[u] = ++ pnt;
    for (int i = head[u]; i != -1; i = a[i].nxt) {
        /*
        这里注意一下：由于我们是从 0 开始将边赋值，所以遍历时有可能出问题。也就是说，如果我们还是按照上文的方法遍历链式前向星，这条边就退化成了有向边，也就出问题了。
		
		hack input : 
		4 4
		4 1
		1 2
		2 3
		3 4   
        */
        int v = a[i].v;
        if (!dfn[v]) {
            fa[v] = u;
            tarjan (v);
            low[u] = min (low[u], low[v]);
            if (low[v] > dfn[u])    vis2[i] = true, vis2[i ^ 1] = true;
            // 与点双类似的标记，位运算符 ^ ，即异或，表示不进位加法 
        } else if (v != fa[u]) {
            low[u] = min (low[u], dfn[v]);
        }
    }
}

void dfs (int u) {
    // dfs 求连通块 
    vis1[u] = true, bcc_pnt[bcc].push_back (u);
    for (int i = head[u]; i != -1; i = a[i].nxt) {
        if (vis1[a[i].v] || vis2[i])    continue;
        dfs (a[i].v);
    }
}

signed main () {
    scanf ("%lld%lld", &n, &m);
    for (int i = 1; i <= n; i ++ )	head[i] = -1;
    for (int i = 1; i <= m; i ++ ) {
        int u, v;
        scanf ("%lld%lld", &u, &v);
        add (u, v), add (v, u);
    }

    for (int i = 1; i <= n; i ++ )
        if (!dfn[i])
            tarjan (i);

    for (int i = 1; i <= n; i ++ )
        if (!vis1[i])
            bcc ++, dfs (i);    // 由于这步是求连通块的数量，所以这里直接累加 bcc 。 

    printf ("%lld\n", bcc);
    for (int i = 1; i <= bcc; i ++ ) {
        printf ("%lld ", bcc_pnt[i].size ());
        for (int j = 0; j < bcc_pnt[i].size (); j ++ )  printf ("%lld ", bcc_pnt[i][j]);
        puts ("");
    }

    return 0;
}

写在最后：

为什么点双不能用边双的方法求呢？因为在图中删除节点，可能会使一些本不是割点的点变为割点。

举个例子，理解一下吧：

这里面，将割点 \(3,5\) 删除，都会导致新的割点产生

---

\(tarjan\) 算法是一个很重要也较难理解的算法。为了加深理解，作此文以记之。

特别鸣谢：

@FeS2_qwq 纠正强连通定义。

@diannaojun 指出边双中遍历边的小瑕疵

\(END\)