统计学习方法笔记

统计学习方法

1.3 统计学习方法的三要素

1.3.1 模型

好，为什么要从1.3开始呢，因为看前面的课，我还没有用到这个软件。

方法=模型+策略+算法

模型有好多个，试试

策略：按照什么样的准则去选取模型

比如说看预测值和真实值差值有多大，或者损失函数最小等

算法 即怎样去实现去寻找这个模型

决策模型

比如房价预测，我输入x，他就会给出一个房价的预测值

条件概率模型

比如我给一张图片，他就会给出属于猫的概率为多少，属于狗的概率为多少

最后呢，我用argmax函数就可以得出属于哪一类了

1.3.2策略

损失函数和风险函数

首先引入损失函数与风险函数的概念。损失函数度量模型一次预测的好坏，风险函数度量平均意义下模型预测的好坏。

损失函数，有误差平方和，等等

平均损失函数

好的，上面这个不用，因为我们知道分布，还要机器学习干什么。

我们用这个 经验损失

当样本足够大时，这俩就差不多了。上面这个就是 损失函数 加起来求平均。L 就是损失函数

在应用中，样本是有限的，所以我们要对平均误差进行矫正。例如正则化什么的，我现在还不会。

经验风险最小化和结构风险最小化

经验风险最小化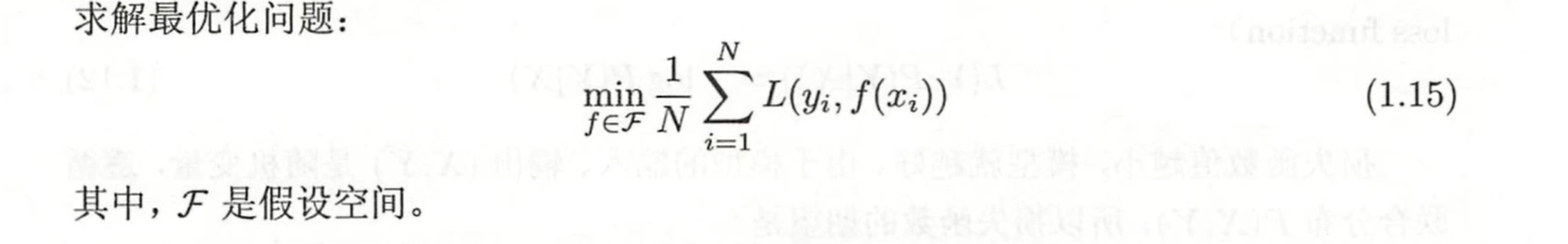

当样本数量少，或者易出现过拟合

我们采用结构风险最小化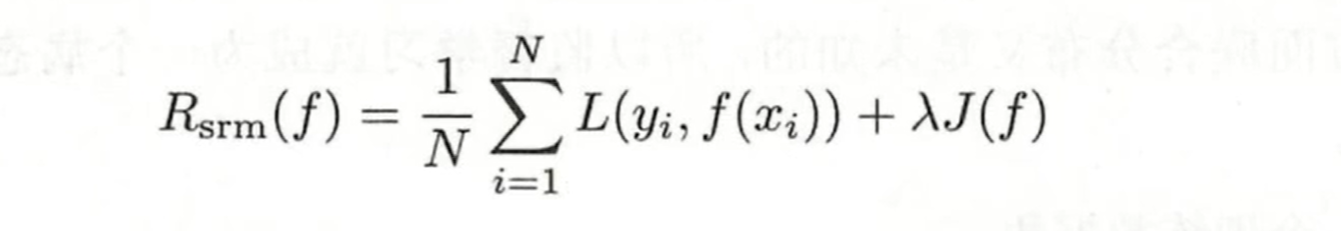，加一项正则化项

对于概率分布的损失函数有

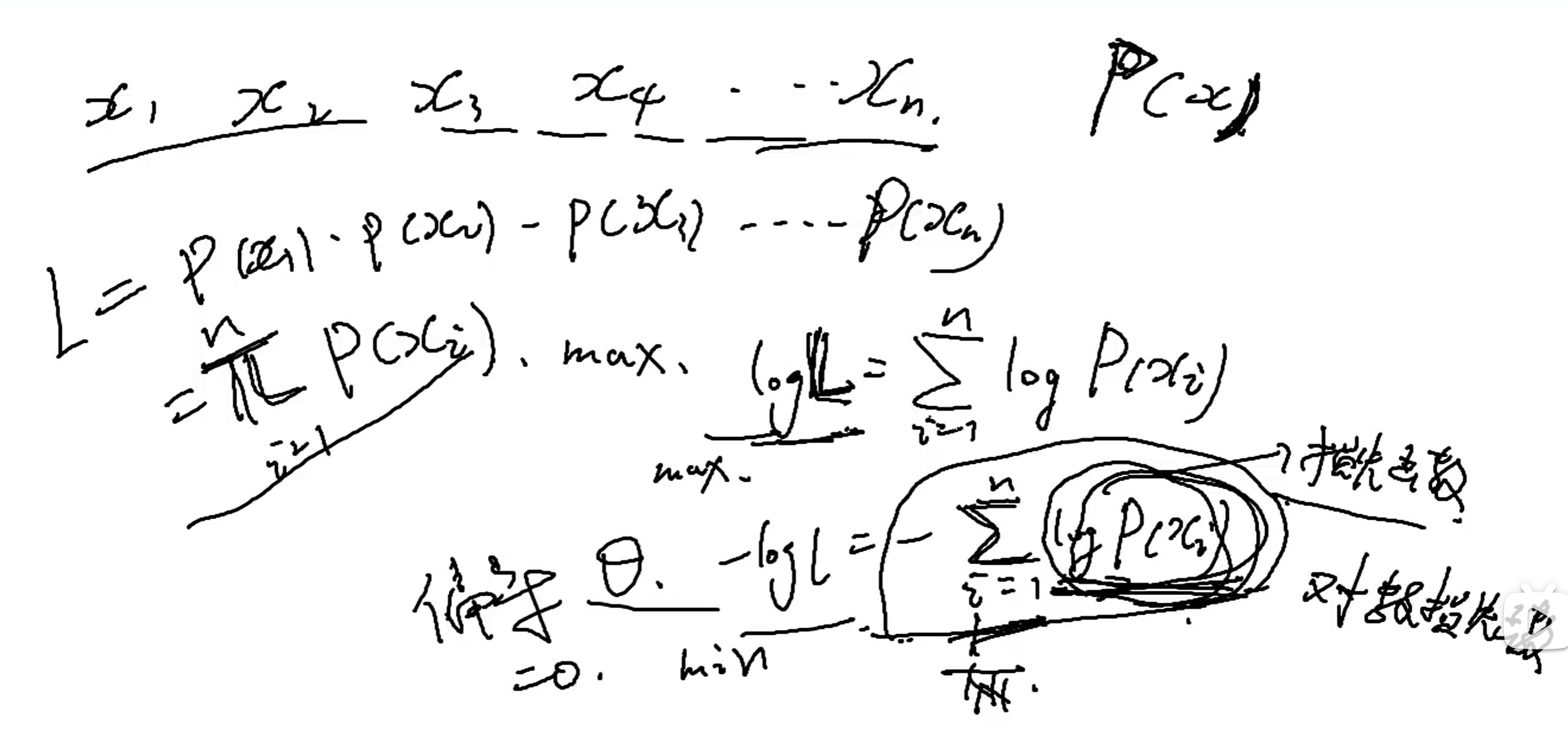
对于这个可以再去别的地方学学

1.3.3算法

算法就是学习模型的具体计算方法。通过算法可以找到最合适的模型

1.4 模型评估与选择

1.4.1 训练与测试误差

训练误差

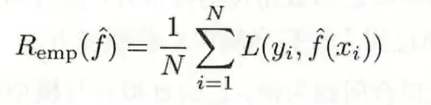
测试误差

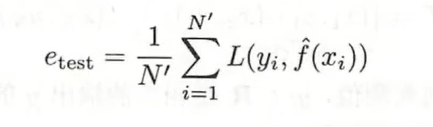
可以理解为考试，在平常的小测试当中，一直做题，做了很多编后，得分很高，但是到了期末考试就，考的很差了，这就是为什么要用到测试误差。

1.4.2过拟合

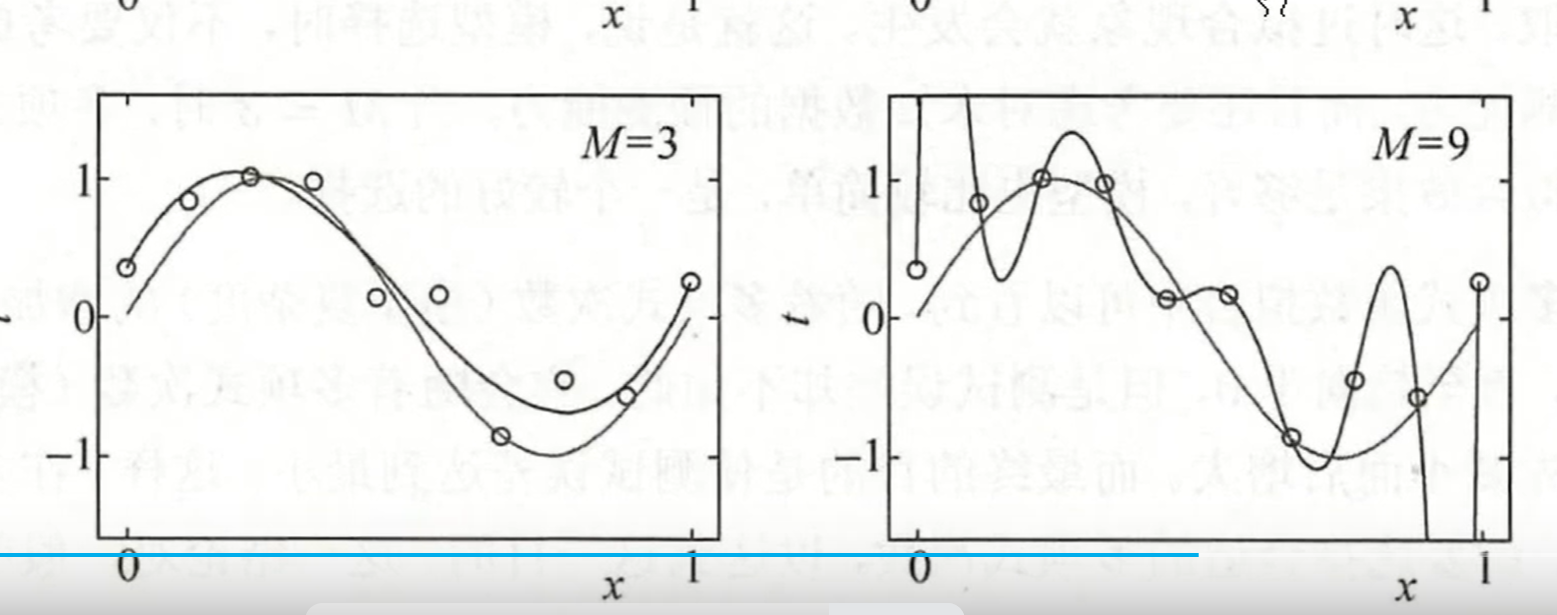
过拟合：是指模型过于复杂，对训练集训练的太好，反而应用到测试集，效果不怎么理想

1.5 正则化与交叉验证

1.5.1 正则化

这里知道正则化是干什么的就可以

后面会说到

用来解决过拟合问题

正则化项一般是模型复杂度的单调递增函数，模型越复杂，正则化值就越大

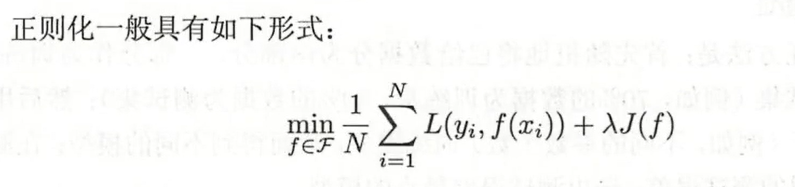
第二项就是正则化项

第二项还可以是以下形式

范数是指

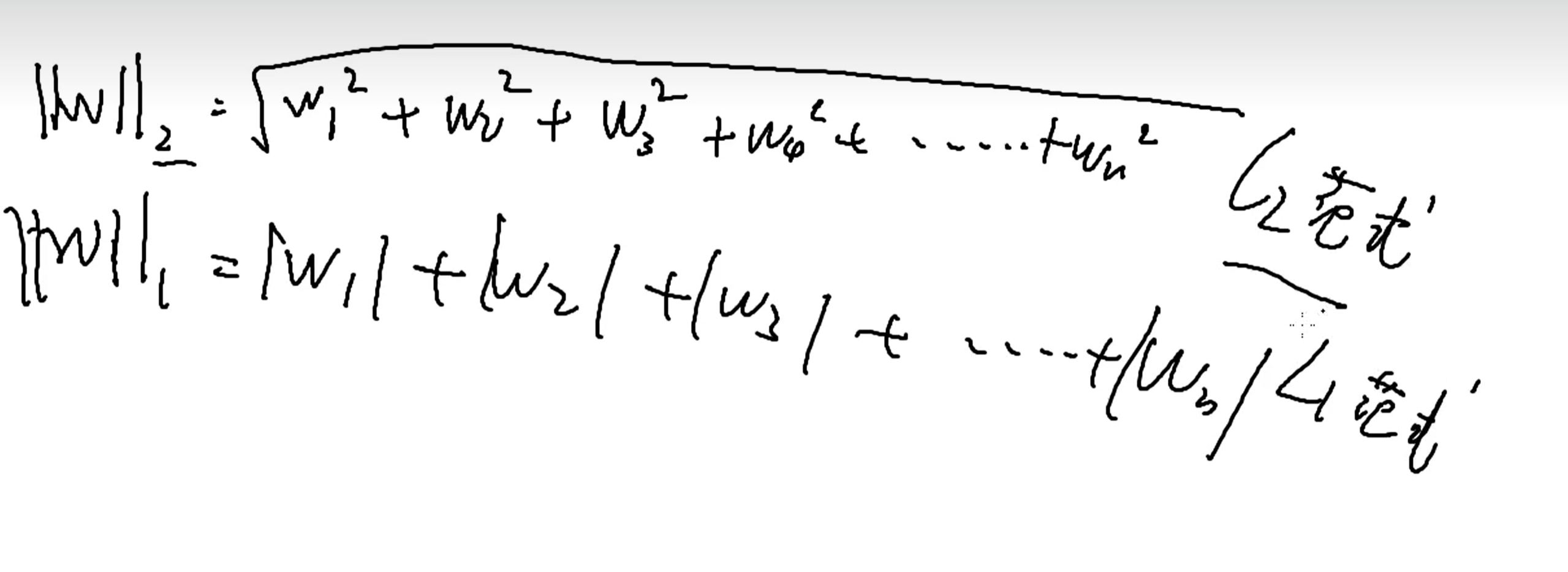
第一行是二范式，就是平方和开根号，第二行是一范式，就是绝对值的和。

为什么正则化会降低过拟合呢。

因为我们引入正则化参数后，整体损失函数，就要考虑到是正则化这一项的值也尽可能的小，而例如正则化参数的取值在一个单位圆或者正方形内，这就导致了其他的参数取值必须符合正则化参数的范围。当然这也会导致准确性降低。

而且正则化在参数更新上会更平滑，在求解过程中，正则化使得训练模型没那么的贴近训练数据，只是贴近训练数据，虽然这看起来，训练效果降低了，但是若是应用在实际当中，过拟合的那个函数反而会效果更差。过拟合的那个太拟合了，把好多噪声都拟合进去了，而正则化虽然有点偏离，但是恰巧的是，刚好有时候也避开了噪声点。

1.5.2 交叉验证

将数据分成S分，取S-1份为训练集,剩下的为测试集。结束后，再取另外的S-1份为训练集，再应用另一个剩下的作测试集。

1.6 泛化能力

1.6.1 泛化误差

泛化能力是指系统对未知数据的预测能力。

泛化误差

当然这个不太好得到，积分形式，可用泛化误差上界来考虑，然后泛化误差上界越小，则模型越好。

1.6.2 泛化误差上界

就是看模型的误差范围小于多少

性质：

推到先不看了，不会

1.7 生成模型与判别模型

生成模型 假设样本不同，分别带到各自模型，谁的概率大，就选谁

判别模型就直接判别ok了

1.8 监督学习

1.8.1 分类问题

分类器判断指标 准确率

二分类分类器的指标是 精确率和召回率

2.1 感知机

感知机是一个二分类线性模型，即输出为实例的类别，一般为其中一类称为正类(+1)(+1)，另一类称为负类(−1)(−1)。可以把上图所示的男孩(+1)(+1)称为正类，女孩(−1)(−1)称为负类。

感知机模型是最基础的，是判别模型

其输出为+1，-1。 其形式为wx+b，其中w是权重和b是偏置

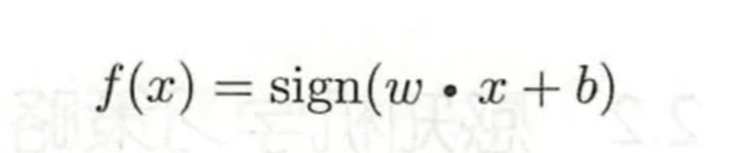
外套了一个sign函数

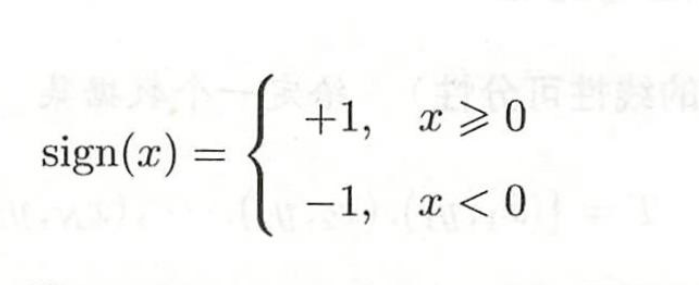
感知机的假设空间就是

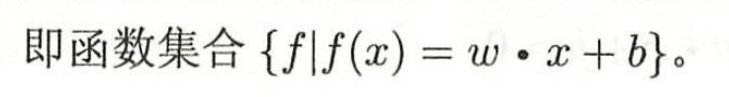
假设空间其实挺吓人的，其含义就是这个函数所有的取值，即不同的w和b，组成的函数空间。

wx+b带入等于零的那个线称为超平面

2.2 感知机学习策略

2.2.1 线性可分和非线性可分

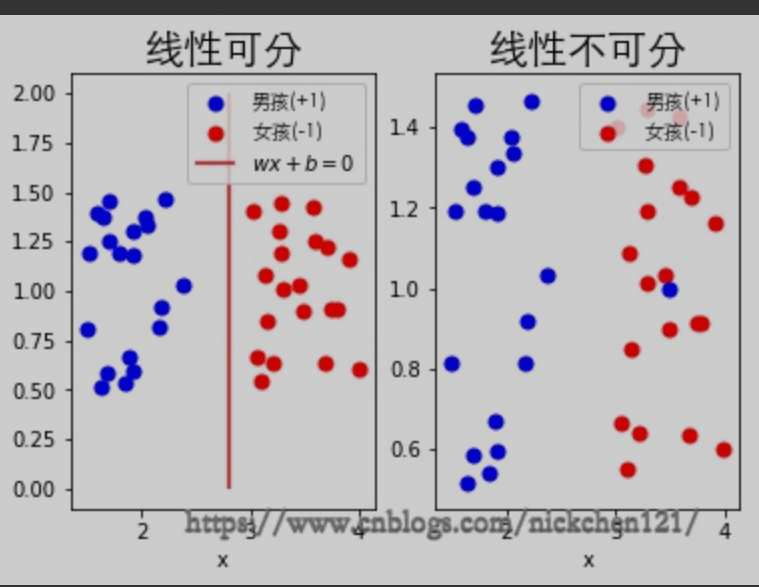
左图可以找到一条直线，即超平面 将这数据集可以完全分开，称为线性可分。而右图，右边女孩混入几个男生，找不到一条超平面将他们分开，则称为非线性可分

2.2 感知机的损失函数 （策略）

把误分类的点到超平面的距离作为损失函数

距离公式为

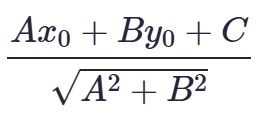
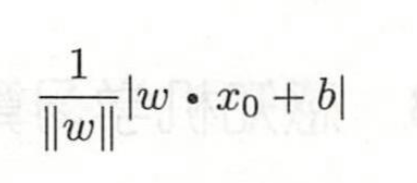
该距离公式源自于数学中点(x0,y0)(x0,y0)到面Ax+By+C=0Ax+By+C=0的公式

这里的分布是指第二范式

进一步变换为

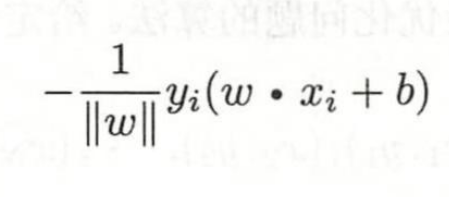
这里yi加上了标签，

然后对所有损失求和

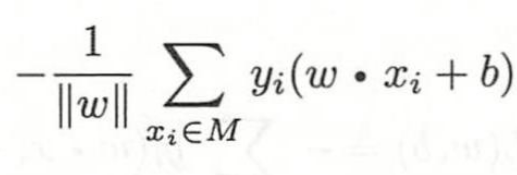
我们可以把分母忽略掉，为什么呢，因为有证明，忽略掉更好计算虽然有影响但是很少。

2.3 算法

然后用梯度下降法去对w，b进行更新

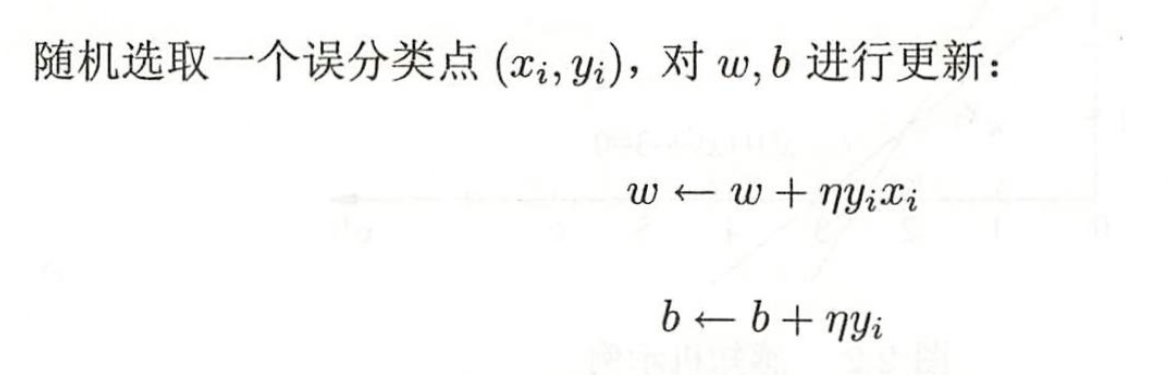
η是学习率

感知机学习算法的原始形式为

在感知机算法中，我们通过调整参数来纠正当前的误分类点，使其能够正确分类，但这个调整有可能会影响到之前已经正确分类的点，导致它们变成新的误分类点。（后面有个b站视频例子，里面有一个计算过程中就出现了，忘记的化可以看一看）这种现象在感知机算法中被称为“震荡”现象，尤其是在训练数据不能被线性分割的情况下（即数据集不可分的情况），这种情况更为常见。

这种学习算法可以理解成，当实例点被误分类后，则调整ω的值，使超平面向靠误分类点的一侧移动，因此减少该误分类点与超平面间的距离，直至超平面越过该误分类点将其分类正确；当实例点分类正确，则不会更新ωω。

2.3.1 感知机的对偶形式

通过随机梯度下降算法可以得到了一个较好的感知机模型，但是如果样本特征较多或者误分类的数据较多，计算将成为该算法的最大的一个麻烦，接下来将介绍计算量较少的感知机最小化目标函数的对偶形式，通过该方法，将极大地减少计算量。

这里的α的迭代

迭代就是多加一次学习次数，相当于原来的多加一次步长

有一个例子 2.3-感知机学习算法 2.3.3-感知机算法的对偶形式 02_哔哩哔哩_bilibili

可以去看看