算法自嘲
Mysql在B+树上的联合索引
二叉查找树:非叶子节点最多拥有两个子节点;非叶子节点的值大于左边子节点,小于右边子节点;没有值相等重复的节点;
平衡二叉树:为了提高二叉查找树的效率,需要平衡;树的左右两边层级不能超过1;查找一个节点的io次数是树的高度,但是频繁的io是个瓶颈,为了解决问题,提出了局部性原理:分为时间局部性和空间 将这部分数据缓存下来。空间局部性原理,当你查询id为1的用户数据的时候,你有很大的概率会去查询id为2,3,4的用户的数据,所以会一次性的把id为1,2,3,4的数据都读到内存中去,这个最小的单位就是页。
OLTP:联机事务处理 --传统的事务处理银行
OLAP:联机分析处理支持复杂查询,提供决策支持 ---基于数据仓库
B树:二叉搜索树;所有非叶子节点至多拥有两个儿子,所有节点存储一个关键字;左小右大
B-树:多路搜索树(非二叉);
- 非叶子节点最多只有M个儿子(M>2)
- 根节点儿子树大于等于2
- 除根节点以外的非叶子节点的儿子数为[M/2, M]
- 每个节点至少m/2-1和至多m-1个关键字
- 非叶子节点的关键字=指向儿子的指针个数-1
- 所有叶子节点位于同一层
B+树上的联合索引:
因为联合索引已经做过排序,第一个索引相同的情况下第二个索引是有序的,所以可以减少一次排序(eg:求一个用户最近三天的购买记录)
也就是说,联合索引(col1, col2,col3)也是一棵B+Tree,其非叶子节点存储的是第一个关键字的索引,而叶节点存储的则是三个关键字col1、col2、col3三个关键字的数据,且按照col1、col2、col3的顺序进行排序
MySql索引那些事
https://mp.weixin.qq.com/s?__biz=MzUxNTQyOTIxNA==&mid=2247484041&idx=1&sn=76d3bf1772f9e3c796ad3d8a089220fa&chksm=f9b784b8cec00dae3d52318f6cb2bdee39ad975bf79469b72a499ceca1c5d57db5cbbef914ea&token=2025456560&lang=zh_CN&scene=21#wechat_redirect
为了获得更好的查询性能设置索引,不加索引需要一行一行去遍历
考虑索引底层存储结构:
二叉数:可能由于数据本身退化成链表
红黑树:树的高度过高导致查询效率变慢。
考虑到磁盘IO和内存使用情况,,mysql在对一个节点的大小设置是16k,
B+树: 把data元素挪走以后,是不是这个节点就能存更多的冗余索引了,意味着分叉就更多了,意味着叶子节点就能存储更多的数据了,而且mysql底层的索引他的根节点,是常驻内存的,直接就放到内存的
索引存放方式
而且mysql底层的索引他的根节点,是常驻内存的,直接就放到内存的
聚集索引/聚簇索引,叶子节点包含了完整的数据记录,InnoDB的主键索引就是一个聚集索引,他的索引和数据是绑定在一起的(叶子节点)。MYISAM的是非聚集索引,索引和数据是分开存储的。InnoDB的主键索引我们叫做聚集索引
多个索引有多个B+树结构,非主键索引叶子节点存储的不是数据,而是主键(一致性和节省空间) 下面是解释:
索引的叶子节点存储的是主键,这是为了节省空间,因为继续存数据的话,那就会导致一份数据存了多份,空间占用就会翻倍。另一方面也是一致性的考虑,都通过主键索引来找到最终的数据,避免维护多份数据导致不一致的情况
链表
一般包含一个数据结构和一个指针,指针一般为next,用来指向下一个结点的位置。
头指针就是链表的名字,仅仅是一个指针,头节点是为了操作的统一和方便建立的放在第一个有效元素结点(首元结点)之前,数据域一般无意义,
插入链表结点
尾插法:新建一个链表结点,链接到当前链表尾指针
中间结点:A1,A2,A5 插入A4,先将A4的next指向A5,再将A2的next指向A4,顺序不能变,否则会丢失A5的寻址方式。
链表头差法:把新的数据的下一个地址改为头节点里存放的地址,这样新的数据就到整个链表的头部了,new->next = head->next ,然后把新的节点的地址给头节点的存放地址区head->next = new
删除结点,找到位置,新建一个指针来保存删除的结点地址,方便在内存中删除,将待删除结点前置结点的next指向删除结点的后面,极为删除。
结点后移:CurrentNode = CurrentNode ->next的表示方法,这是将CurrentNode ->next这个结点的指针移动到了当前这个结点CurrentNode,下一次使用CurrentNode指针的时候CurrentNode实际已经指向了下一个结点CurrentNode ->next。
获取链表元素:给定值和给定位置都需要遍历链表,在给定元素值的情况下,定义一个元素序号随着遍历的过程累加,遍历的过程校验链表的结点是否与给定的元素匹配,如果匹配则返回元素位置的序号;在给定位置的情况下就更简单一些,元素序号(我们定义的序号)累加到对应位置,返回对应结点的元素即可。
链表的反转和是否有环~~~~~
HashMap和ConcurrentHashMap
Hashmap实现hash表的效果,尽量实现O(1)级别的增删改查,同时使用了数组和链表,j8加入了红黑树,最外层是数组,数组的每一个元素是一个列表的表头。初始化大小和加载因子,初始大小用来规定哈希表数组的长度,即桶的个数。加载因子用来表示哈希表元素的填满程度,越大则表示允许填满的元素就越多,哈希表的空间利用率就越高,但是冲突的机会也就增加了。反之,越小则冲突的机会就会越少,但是空间很多就浪费了。
对于新插入的数据或者待读取的数据,HashMap将Key的哈希值对数组长度取模,结果作为该Entry在数组中的index。在计算机中,取模的代价远高于位操作的代价,因此HashMap要求数组的长度必须为2的N次方,那么n-1的低位就全是1,哈希值进行与操作时可以保证低位的值不变,从而保证分布均匀,效果等同于hash%n,此时将Key的哈希值对2^N-1进行与运算,其效果即与取模等效。
Key的hash值直接决定了值的分布和是否冲突,可能出现低位相同,高位不同,与2^N-1取与后的结果都相同,还是通过位操做使二进制形式中的1尽量均匀分布从而尽可能减少哈希冲突。
扩容的时候一般扩大两倍,保证寻址方式任然适用。
ReSize–rehash:
Hash公式为:key的hash进行高16位和低16位的异或操作,降低哈希冲突的可能性
索引计算公式:index=HashCode(key)&(Capacity-1)
Fast-fail:当HashMap的iterator()方法被调用时,会构造并返回一个新的EntryIterator对象,并将EntryIterator的expectedModCount设置为HashMap的modCount(该变量记录了HashMap被修改的次数)。
插入数据:
扩容:扩大两倍后,判断无后继结点,获取在新数组中的位置,有是树则拆树,是列表则拆列表。
树化操作:
- 为何单链表转化为红黑树,要求节点个数大于8?
- 为何转化为红黑树前,要求数组总长度要大于64?
- 为何红黑树转化为单链表,要求节点个数小于等于6?
Resize扩容导致出现环
在线程1操作时,e指向key3,next指向key7,线程1休眠。线程2开始操作,完成后key7和key3位置颠倒,此时线程1开始,方法中走后next = e 导致e指向key7,下次循环next = e.next导致next指向key3 造成环
ConcurrentHashMap
ConcurrentHashMap最外层不是一个大的数组,而是一个Segment的数组。每个Segment包含一个与HashMap数据结构差不多的链表数组。
Segment继承自ReentrantLock,所以我们可以很方便的对每一个Segment上锁。
Segment获取:Segment<K,V> s = (Segment<K,V>)UNSAFE.getObjectVolatile(segments, u)
HashEntry获取:HashEntry<K,V> e = (HashEntry<K,V>) UNSAFE.getObjectVolatile
(tab, ((long)(((tab.length - 1) & h)) << TSHIFT) + TBASE)
在做size全部上锁操作时,不仅无法对Map进行写操作,同时也无法进行读操作,不利于对Map的并行操作。
为更好支持并发操作,ConcurrentHashMap会在不上锁的前提逐个Segment计算3次size,如果某相邻两次计算获取的所有Segment的更新次数(每个Segment都与HashMap一样通过modCount跟踪自己的修改次数,Segment每修改一次其modCount加一)相等,说明这两次计算过程中无更新操作,则这两次计算出的总size相等,可直接作为最终结果返回。如果这三次计算过程中Map有更新,则对所有Segment加锁重新计算Size。
- ConcurrentHashMap线程安全,而HashMap非线程安全
- HashMap允许Key和Value为null,而ConcurrentHashMap不允许
- HashMap不允许通过Iterator遍历的同时通过HashMap修改,而ConcurrentHashMap允许该行为,并且该更新对后续的遍历可见
链表
线性表
顺序存储结构和链式存储结构。顺序存储结构的创建其实就是数组的初始化,
Set
TreeSet没有get方法
堆
堆是一个完全二叉树,堆能实现比排序更快速的寻找指定长度最大值
像大小为 k 的堆中添加元素的时间复杂度为 O(logk)
若将和此次序列对应的一维数组(即以一维数组作此序列的存储结构)看成是一个完全二叉树,则堆的含义表明,完全二叉树中所有非终端结点的值均不大于(或不小于)其左、右孩子结点的值。由此,若序列{k1,k2,…,kn}是堆,则堆顶元素(或完全二叉树的根)必为序列中n个元素的最小值(或最大值)。
栈
用数组实现栈和队列,都使用贪心算法,不同之处在于:队列是先进先出,当移除数个元素后,队列的数据是存储在中间位置的,让队尾数据id-对首数据id得到现在的队中数据,数据为数组长度的四分之一时,数组减半,队列数据移动到最最左端
树
BST二叉搜索树
- 所有非叶子节点最多拥有两个孩子
- 所有节点存储一个关键字
- 非叶子节点左指针指向小于其关键字的子数,右指针指向大于其关键字的子数
- 左右子数的深度之差不超过1
- 左右子树任为平衡二叉树,平衡因子BF=左子树深度-右子树深度
AVL平衡二叉树
RBT红黑数
AVL是严格搜索二叉树,红黑树用非严格的平衡来换取旋转次数的降低,搜索次数远远大于插入可用AVL,差不多可用红黑数。
红黑数每个节点内含五个域,color,key,left,right,p。如果相应的指针域没有,则为null
- 节点是红色或者黑色
- 根节点是黑色
- 每个红色节点的两个孩子都是黑色
- 从任意一节点到起叶子都包含相同的黑色节点
B树
B-树
是一种平衡多路搜索数(并不是二叉的):
- 定义任意非叶子节点做多只有M个儿子(M>2)
- 根节点的儿子个数为[2,m]
- 除根节点以外的非叶子节点的儿子个数[M/2,M]
- 每个节点存放至少M/2-1(向上取整)个关键字,至多M-1个关键字
- 非叶子节点的关键字个数=指向儿子的指针个数-1
- 非叶子节点关键字:k[i]<k[i+1]
- 非叶子节点指针:p[1]指向关键字小于k[1]的子树,p[M]指向关键字大于k[M-1]的子树,其他的p[i]指向关键字属于(k[i-1],k[i])的子树
- 所有叶子节点位于同一层
B+树
是B-数的一种变体
- 和B-数的基本定义相同
- 非叶子节点的子指针与关键字个数相同
- 非叶子节点的子树指针P[i],指向关键字值属于[K[i],K[i+1]]的子树
- 为所有的叶子节点增加一个链指针
- 所有关键字都在叶子节点出现
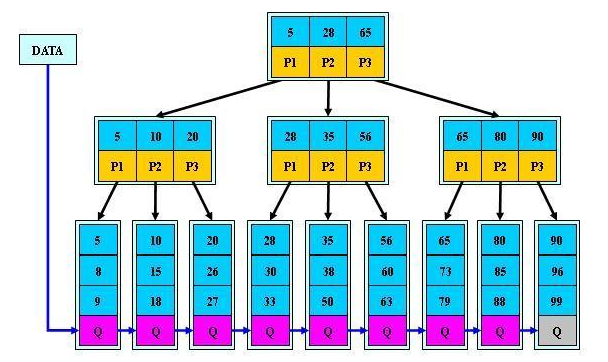
B+特性
- 所有关键字都出现在叶子节点中(稠密索引),且链表中的关键字恰好是有序的
- 不可能在非叶子节点中命中
- 非叶子节点相当于叶子节点的索引(稀疏索引),叶子节点相当于存储数据的数据层,叶子节点都带有指向下一个节点的指针,是一个有序链表
- 更适合文件索引系统
B-树和B+树的区别
1)B+树查询时间复杂度固定是logn,B-树查询复杂度最好是 O(1)。
2)B+树相邻接点的指针可以大大增加区间访问性,可使用在范围查询等,而B-树每个节点 key 和 data 在一起,则无法区间查找。
3)B+树更适合外部存储,也就是磁盘存储。由于内节点无 data 域,每个节点能索引的范围更大更精确
在查询上B+树的中间节点没有存储数据,所以在同样大小的磁盘叶B+树可以存放更多节点元素,比B-树更加矮胖,磁盘IO更少,又因为B+树叶子节点都带有指针,范围查询更加高效
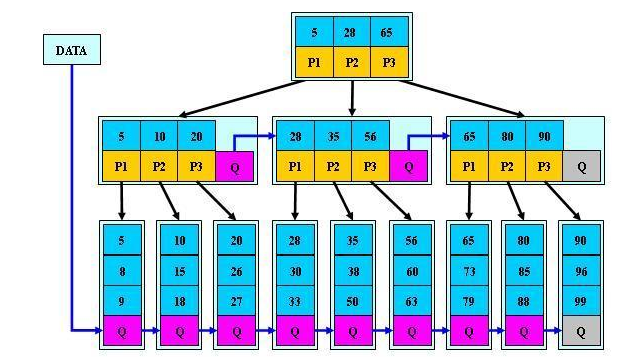
B*树
B树是B+树的变形,在非根和非叶子节点再增加指向兄弟的指针,B树定义了非叶子节点关键字个数至少为2/3M,即块的最低使用率为2/3,代替B+树的1/2
B+树在分裂的时候会将原来的数据的二分之一复制到新节点,不会影响到兄弟,当B树节点满时,如果兄弟节点未满,会将一部分数据移动到兄弟节点上,修改父节点的兄弟节点的关键字,如果兄弟满了,就将三分之一的数据复制到新节点上。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号