FFT学习笔记
FFT学习笔记
前置知识:
- 复数的基础概念。
- 可以看我这篇博文复数基础知识。
前言:
- 假设我们现在有一个\(n-1\)次多项式,通项为\(\sum_{i=0}^na_i*x^i\)。
- 比如:\(A(x)=x^2+2x+1,B(x)=3x^3+2x^2+5x+1\)。
- 我们想将这两个多项式相乘,采用朴素算法只能老老实实的将每一项对应相乘再相加,时间复杂度达到了\(O(nm)\)。
- 当然可以转换一种思路,将\(n\)个不同的\(x\)带入这个\(n-1\)次多项式,会取得不同的\(y\),这\(n个\)点\((x,y)\)唯一确定了这个多项式。
- 这里我们可以发现,两个用点值表示的多项式相乘,我们如果\(O(n)\)的时间枚举一下\(x_i\),可以得到:\(C(x_i)=A(x_i)*B(x_i)\)。
- 这样可以在\(O(n)\)的时间内完成多项式乘法。(因为\(n\)个点可以唯一的确定一个\(n-1\)次多项式)
- 但是可惜的是,取\(x_i\)求\(A(x_i)\),这样的复杂度是\(O(n)\)的,如果取\(n\)个\(x\),那整体复杂度就是\(O(n^2)\)的,和朴素枚举差不多。
- 但如果可以快速的将多项式转换为点值表示(以及其反向操作),之后就可以快速地完成多项式乘法。
- 快速傅里叶变换\((FFT)\)是一种能在\(O(nlogn)\)的时间内将一个多项式转换成点值表示的算法。
- 所以算法流程是这样的:
- 将两个式子从系数用\(O(nlogn)\)时间表示转化为点值表示。
- 然后以\(O(n)\)的时间完成两个式子相乘。
- 最后以\(O(nlogn)\)时间将点值表示再转换为多项式系数表示。
几个容易混淆的缩写:
- \(DFT:\)离散傅里叶变换,\(O(n^2)\),\(FFT\)的朴素版。
- \(FFT:\)快速傅里叶变换,\(O(nlogn)\).
- \(FNTT/NTT:FFT\)的升级版。
- \(FWT:\)快速沃尔什变换。
单位根:
-
下文中,默认\(n\)为\(2\)的正整数次幂。
-
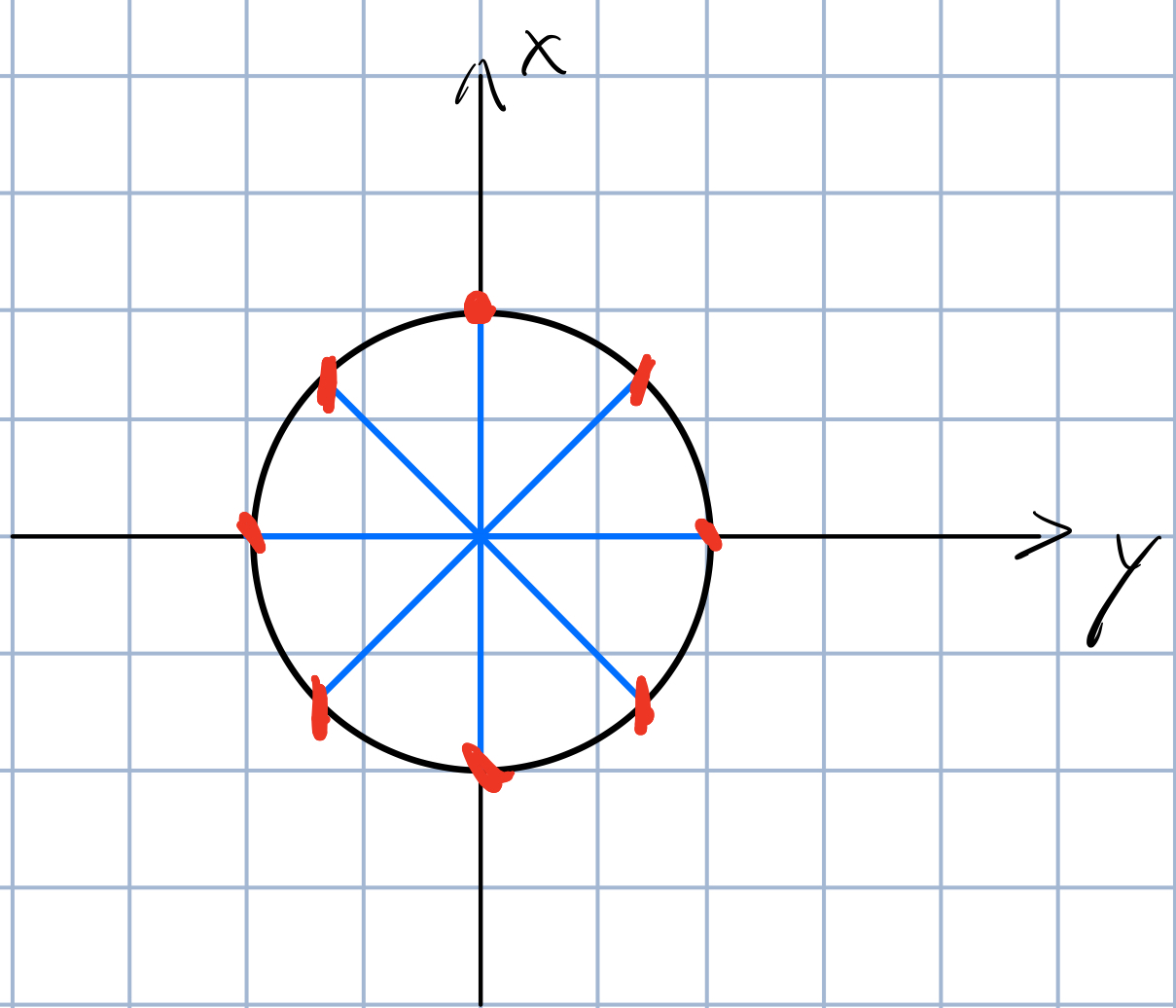
在二维平面,原点为圆心,\(1\)为半径做圆,所得圆为单位圆。
-
那么我们先把圆切成\(n\)等份,然后对应\(n\)个向量。
-
画个图看看吧:
-
![]()
-
这样就把一个单位圆分为了\(8\)等份。
-
根据上一篇博文的知识,其实这就是\(z=e^{i}\)开了\(n\)次方。
-
\(\sqrt[n]{z}=e^{i\frac{2k\pi}{n}}=cos\frac{2k\pi}{n}+isin\frac{2k\pi}{n}\)。
-
我们设\(w_n^k=e^{i\frac{2k\pi}{n}}\).
-
\(w_n^0=e^{0}=cos0+isin0,w_n^1=e^{\frac{i2\pi}{n}}=cos\frac{2\pi}{n}+isin\frac{2\pi}{n},...,\)
-
\(w_n^{n-1}=e^{i2(n-1)\pi}=cos\frac{2(n-1)\pi}{n}+isin\frac{2(n-1)\pi}{n}\).
-
也就对应的是圆上的几个点。
单位根的性质:
- \(1:w_{2n}^{2k}=w_n^k\).
- 证明:\(w_{2n}^{2k}=e^{i\frac{2(2k)\pi}{2n}}=e^{i\frac{2k\pi}{n}}=w_n^k\).证毕。
- \(2:w_n^{k+\frac{n}{2}}=-w_n^k\).
- 就相当于一个点\(+\frac{n}{2}\)变成对面那个点,也就是这个点的反方向。
- 或者也可以用欧拉公式展开一下用三角函数变换证明。(我太懒了)
快速傅里叶变换:
- 我们知道一个\(n-1\)次多项式可以被\(n\)个点确定。
- 假设\(A(x)=(a_0,a_1,...,a_{n-1})\)。
- 那么有\(A(x)=a_0+a_1x+a_2x^2+...+a_{n-1}x^{n-1}\)。
- 接下来按照下标奇偶性分类。
- \(A(x)=(a_0+a_2x^2+a_4x^4+...+a_{n-2}x^{n-2})+(a_1x+a_3x^3+...+a_{n-1}x^{n-1})\).
- 设
- \(A_1(x)=a_0+a_2x+a_4x^2+...+a_{n-2}x^{\frac{n}{2}-1}\).
- \(A_2(x)=a_1+a_3x+a_5x^2+...+a_{n-1}x^{\frac{n}{2}-1}\).
- 那么有:
- \(A(x)=A_1(x^2)+xA_2(x^2)\).
- 将\(w_n^k(k<\frac{n}{2})\)代入得:
- \(A(w_n^k)=A_1(w_n^{2k})+w_n^kA_2(w_n^{2k})\).
- 同理将\(w_n^{k+\frac{n}{2}}\)代入得:
- \(A(w_n^{k+\frac{n}{2}})=A_1(w_n^{2k+n})+w_n^{k+\frac{n}{2}}A_2(w_n^{2k+n})\).
- \(=A_1(w_n^{2k}*w_n^n)-w_n^kA_2(w_n^{2k}*w_n^n)\).
- \(=A_1(w_n^{2k})-w_n^kA_2(w_n^{2k})\).
- 可以发现,这两个式子只有一个常数项不同。
- 也就是在枚举第一个式子的时候,可以\(O(1)\)的得到第二个式子的值。
- 而我们又知第一个式子中\(k\in[0,\frac{n}{2}-1],k+\frac{n}{2}\in[\frac{n}{2},n-1]\).
- 所以也就是将原问题缩小了一半。
- 满足分治性质,递归后合并求解即可。
- 于是就做到了在\(O(nlogn)\)时间完成了多项式的系数表示到点值表示。
快速傅里叶逆变换:
-
接下来我们需要将点值表示法还原回系数表示,这个过程为傅里叶逆变换。
-
我们先假设\((y_0,y_1,...,y_{n-1})\)为多项式\(A(x)=a_0+a_1x+a_2x^2+...+a_{n-1}x^{n-1}\)为\(A(x)\)的离散傅里叶变换。
-
再设\(B(x)=y_0+y_1x+y_2x^2+...+y_{n-1}x^{n-1}\),现在我们代入单位根的倒数\(w_n^0,w_n^{-1},w_n^{-2},...,w_n^{-(n-1)}\)可以得到一个新的离散傅里叶变换\((z_0,z_1,...,z_{n-1})\)。
-
可以得到
- \(z_k=y_0+y_1(w_n^{-1})^1+y_2(w_n^{-2})^2+...+y_{n-1}(w_n^{-(n-1)})^{n-1}=\sum_{i=0}^{n-1}y_i(w_n^{-k})^i\).
- \(=\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_j(w_n^i)^j)(w_n^{-k})^i\).
- \(=\sum_{j=0}^{n-1}a_j(\sum_{i=0}^{n-1}(w_n^{j-k})^i)\).
-
可以看一下\(\sum_{j=0}^{n-1}(w_n^{j-k})^i\)。当\(j-k=0\)时,它等于\(n\);其余的时候,可通过等比数列求和得知:
- \(\frac{(w_n^{j-k})^n-1}{w_n^{j-k}-1}=\frac{(w_n^n)^{j-k}-1}{w_n^{j-k}-1}=\frac{1^{j-k}-1}{w_n^{j-k}-1}=0\).
-
那么就可以得知:\(z_k=na_k\).
- \(a_i=\frac{z_i}{n}\).
-
所以我们可以得到一个结论。多项式\(A(x)\)的离散傅里叶变换的另一个多项式\(B(x)\)的系数,取单位根的倒数\(w_n^0,w_n^{-1},...,x_n^{-(n-1)}\)作为\(x\)代入\(B(x)\),得到的每个数再除以\(n\),得到的是\(A(x)\)的各项系数。这就实现了傅里叶逆变换。
-
至此\(FFT\)的理论基础已结束。
代码实现:
-
根据上述分析可得,一个序列需要划分成两部分后分治递归即可。
-
但是可以再度优化。
-
![]()
-
可以发现原序列和后序列分组其实是按照原序列下标的二进制翻转。
-
因此按照下标进行奇偶性分类是没有必要的,于是我们可以免去递归的过程。
-
对于二进制翻转要怎么做呢?
-
这是一个\(trick:\)蝴蝶定理。
-
假设即将反转的数字为\(i\),在\(i\)之前的数字都已经翻转好了。
-
那么对于\(i\)来说就是右移后翻转后再右移,如果是奇数为在最高位补\(1,\)也就是\(r[i] = (r[i>>1]>>1)|((i\&1)<<(l-1))\)。
-
弄不明白可以手摸几个例子。
-
之后直接枚举子区间后向上合并即可。
-
枚举分割的中点的时间复杂度为\(O(logn)\),合并复杂度为\(O(n)\),总时间复杂度为\(O(nlogn)\)。
-
#include<bits/stdc++.h> using namespace std; const int maxn = 1e7 + 10; const double PI = acos(-1.0); int n, m, limit, l, r[maxn]; inline int read() { char c = getchar(); int x = 0, f = 1; while (c < '0' || c > '9') {if (c == '-')f = -1; c = getchar();} while (c >= '0' && c <= '9') {x = x * 10 + c - '0'; c = getchar();} return x * f; } //手写复数类 struct Complex { double x, y; Complex (double xx=0, double yy=0){ x = xx; y = yy; } Complex operator + (const Complex b) const{ return Complex(x+b.x, y+b.y); } Complex operator - (const Complex b) const{ return Complex(x-b.x, y-b.y); } Complex operator * (const Complex b) const{ return Complex(x*b.x-y*b.y, x*b.y+y*b.x); } }a[maxn], b[maxn]; void fft(Complex c[], int type) { for(int i = 0; i < limit; i++) if(i < r[i]) swap(c[i], c[r[i]]); //枚举待合并区间的中点的长度 for(int mid = 1; mid < limit; mid <<= 1) { //设立单位根 Complex wn(cos(PI/mid), type*sin(PI/mid)); //R是区间的长度,j表示当前已经到哪个位置了,而且是左端点 for(int R = mid<<1, j = 0; j < limit; j += R) { Complex w(1, 0); //初始幂次 for(int k = 0; k < mid; k++, w = w*wn) //枚举左半部分 { Complex x = c[j+k], y = w*c[j+mid+k]; c[j+k] = x+y; c[j+mid+k] = x-y; //右半部分减去即可 } } } } int main() { //1e6的读入,需要写快读 n = read(), m = read(); for(int i = 0; i <= n; i++) a[i].x = read(); for(int i = 0; i <= m; i++) b[i].x = read(); limit = 1; //要求limit一定是2的整次幂 while(limit <= n+m) limit <<= 1, l++; for(int i = 0; i < limit; i++) r[i] = (r[i>>1]>>1)|((i&1)<<(l-1)); //对a序列和b序列分别处理 fft(a, 1); fft(b, 1); for(int i = 0; i <= limit; i++) a[i] = a[i]*b[i]; fft(a, -1); for(int i = 0; i <= n+m; i++) //四舍五入 printf("%d ", (int)(a[i].x/limit+0.5)); return 0; }





 浙公网安备 33010602011771号
浙公网安备 33010602011771号