POJ 1837 Balance

POJ 1837 Balance

题意:

一个天平上有 \(C(2<=C<=20)\) 个挂钩，挂钩所在位置在区间 \([-15,15]\)。

你的手里有 \(G(2<=G<=20)\)个砝码，每个砝码的重量在区间 \([1,25]\) 。

求天平平衡的方法数。

思路:

根据物理知识可得 : 重量 = 力矩 * 重量

状态定义?

显然，当我们加入一个新砝码的时候，需要知道放入之前已有的天平对应的平衡数值。

定义 \(f[i][j]\) 为遍历到第 \(i\) 个物品，当前天平的平衡值为 \(j\) 的方案数。

因为可能出现负数，所以这里采用 \(basic = 7501\) （根据极限情况取得）来校准。

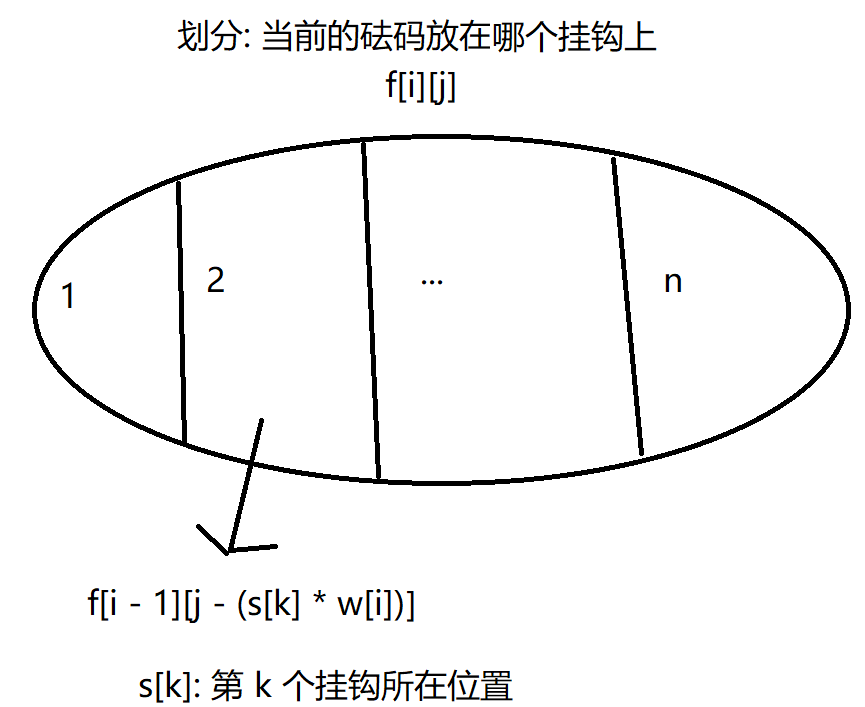
转移方程: \(f[i][j]\; += \sum_{k = 1} ^n f[i - 1][j - s[k] * w[i]]\)

实现:

#include <cstdio>
#include <algorithm>
using namespace std;
// 重量 = 力矩 * 重量
const int N = 25, basic = 7501, M = 2e4, INF = 2e5;
int a[N], w[N];
int f[N][M];
int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    for (int i = 1; i <= m; i++)
        scanf("%d", &w[i]);

    f[0][basic] = 1;
    // 遍历物品
    for (int i = 1; i <= m; i++)
    {
        // 遍历差值
        for (int j = 0; j < M; j++)
        {
            // 遍历放的位置
            for (int k = 1; k <= n; k++)
            {
                int sum = j - a[k] * w[i];
                if (sum >= 0 && sum < M)
                {
                    f[i][j] += f[i - 1][sum];
                }
            }
        }
    }
    printf("%d\n", f[m][basic]);
    return 0;
}